Средняя кинетическая энергия частиц газа

Оказывается, что ключевую роль в описании идеального газа играет средняя кинетическая энергия его частиц.

Частицы газа двигаются с разными скоростями. Пусть в газе содержится N частиц, скорости которых равны v₁,v₂,...,v_N. Масса каждой частицы равна m₀. Кинетические энергии частиц:

.

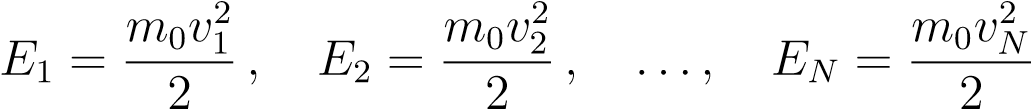Средняя кинетическая энергия E частиц газа — это среднее арифметическое их кинетических энергий:

.

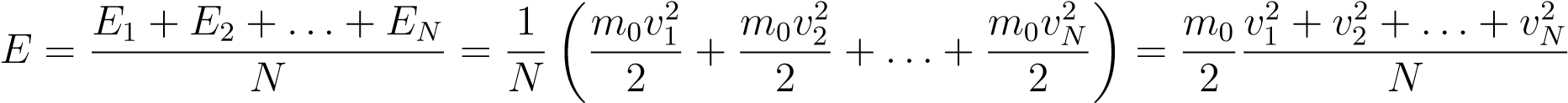Последний множитель — это средний квадрат скорости, обозначаемый просто v²:

.

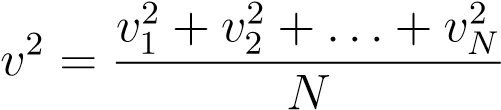Тогда формула для средней кинетической энергии приобретает привычный вид:

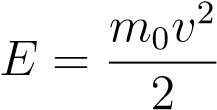. (1)

Корень из среднего квадрата скорости называется средней квадратической скоростью:

.

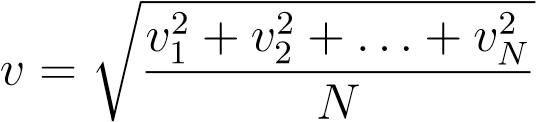Основное уравнение МКТ идеального газа

Cвязь между давлением газа и средней кинетической энергией его частиц называется основным уравнением молекулярно-кинетической теории идеального газа. Эта связь выводится из законов механики и имеет вид:

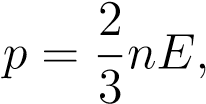
где n — концентрация газа (число частиц в единице объёма). С учётом (1) имеем также:

.

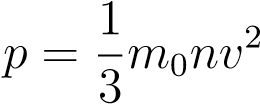Что такое m₀n? Произведение массы частицы на число частиц в единице объёма даёт массу единицы объёма, то есть плотность: m₀n = ρ. Получаем третью разновидность основного уравнения:

.

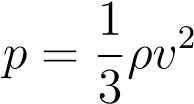Энергия частиц и температура газа

Можно показать, что при установлении теплового равновесия между двумя газами выравниваются средние кинетические энергии их частиц. Но мы знаем, что при этом становятся равны и температуры газов. Следовательно, температура газа — это мера средней кинетической энергии его частиц.

Собственно, ничто не мешает попросту отождествить эти величины и сказать, что температура газа — это средняя кинетическая энергия его молекул. В продвинутых курсах теоретической физики так и поступают. Определённая таким образом температура измеряется в энергетических единицах — джоулях.

Но для практических задач удобнее иметь дело с привычными кельвинами. Связь средней кинетической энергии частиц и абсолютной температуры газа даётся формулой:

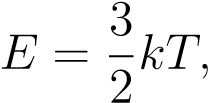(2)

где k = 1,38 · 10⁻²³ Дж/К — постоянная Больцмана.

Из данной формулы можно получить выражение для средней квадратической скорости частиц. Подставим (1) в (2):

откуда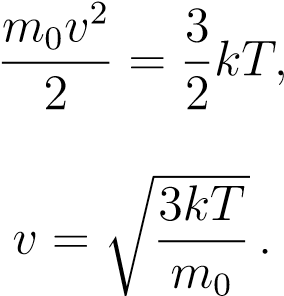

В эту формулу входит масса частицы m₀, которую ещё надо вычислить. Но можно получить более удобный вариант формулы, домножив числитель и знаменатель подкоренного выражения на число Авогадро N_A:

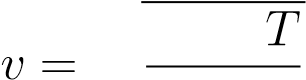r3kNA

.

m0NA

В знаменателе имеем: m₀N_A = µ — молярная масса газа. В числителе стоит произведение двух констант, которое также является константой:

Дж Дж

−23 23 −1

R = kN_A = 1,38 · 10 · 6,02 · 10 моль = 8,31 .

К моль · К

Константа R называется универсальной газовой постоянной.

Теперь формула для средней квадратической скорости приобретает вид:

.

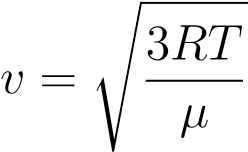Такое выражение гораздо более удобно для практических вычислений.