Вероятность. теоремы сложения и умножения вероятностей

Основные понятия комбинаторики

В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, 3,: , 9 и составлять из них комбинации, то будем получать различные числа, например 143, 431, 5671, 1207, 43 и т.п.

Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (например, 143 и 431), другие - входящими в них цифрами (например, 5671 и 1207), третьи различаются и числом цифр (например, 143 и 43).

Таким образом, полученные комбинации удовлетворяют различным условиям.

В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.

Предварительно познакомимся с понятием факториала.

Произведение всех натуральных чисел от 1 до n включительно называют n-факториаломи пишут .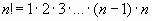

Пример 1.

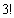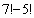Вычислить: а) ; б) ; в) .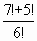

Решение. а) .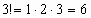

б) Так как 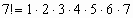и 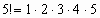, то можно вынести за скобки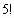

Тогда получим

.

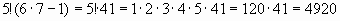в) .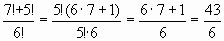

Перестановки.

Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.

Перестановки обозначаются символом Р_n, где n- число элементов, входящих в каждую перестановку. (Р - первая буква французского слова permutation- перестановка).

Число перестановок можно вычислить по формуле

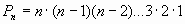
или с помощью факториала:

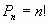
Запомним, что 0!=1 и 1!=1.

Пример 2. Сколькими способами можно расставлять на одной полке шесть различных книг?

Решение. Искомое число способов равно числу перестановок из 6 элементов, т.е.

.

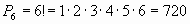Размещения.

Размещениями из m элементов в n в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком из расположения.

Размещения обозначаются символом 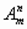, где m- число всех имеющихся элементов, n- число элементов в каждой комбинации. (А-первая буква французского слова arrangement, что означает "размещение, приведение в порядок").

При этом полагают, что n 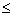m.

Число размещений можно вычислить по формуле

,

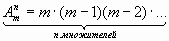т.е. число всех возможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m.

Запишем эту формулу в факториальной форме:

.

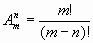Пример 3. Сколько вариантов распределения трех путевок в санатории различного профиля можно составить для пяти претендентов?

Решение. Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е.

.

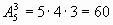Сочетания.

Сочетаниями называются все возможные комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом (здесь m и n-натуральные числа, причем n 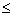m).

Число сочетаний из m элементов по n обозначаются 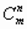(С-первая буква французского слова combination - сочетание).

В общем случае число из m элементов по n равно числу размещений из m элементов по n, деленному на число перестановок из n элементов:

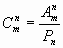
Используя для чисел размещений и перестановок факториальные формулы, получим:

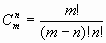
Пример 4. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

Решение. Так как порядок выбранных четырех человек не имеет значения, то это можно сделать 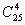способами.

Находим по первой формуле

.

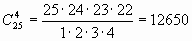Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:

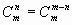
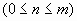
(по определению полагают 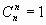и );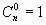

.

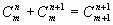Решение комбинаторных задач

Задача 1. На факультете изучается 16 предметов. На понедельник нужно в расписание поставить 3 предмета. Сколькими способами можно это сделать?

Решение. Способов постановки в расписание трех предметов из 16 столько, сколько можно составить размещений из 16 элементов по 3.

.

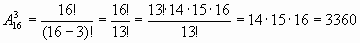Задача 2. Из 15 объектов нужно отобрать 10 объектов. Сколькими способами это можно сделать?

Решение.

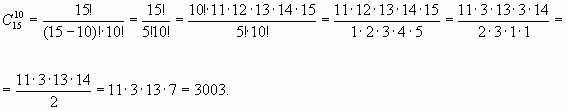
Задача 3. В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно?

Решение.

.

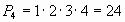Задача 4. Сколькими способами можно составить дозор из трех солдат и одного офицера, если имеется 80 солдат и 3 офицера?

Решение. Солдат в дозор можно выбрать

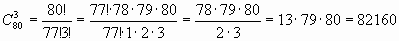
способами, а офицеров 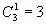способами. Так как с каждой командой из солдат может пойти любой офицер, то всего имеется 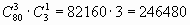способов.

Задача 5. Найти 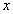, если известно, что .

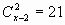Решение.

Так как 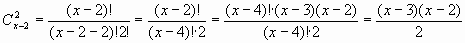, то получим

,

,

,

, .

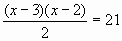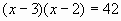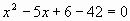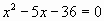
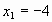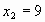По определению сочетания следует, что 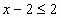, 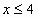. Т.о. .

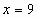Ответ: 9