Раздел ii. молекулярная физика. термодинамика

ОСНОВНЫЕ ФОРМУЛЫ

1. Количество вещества однородного газа (в молях):

,

где N - число молекул газа, N_А - число Авогадро, m -масса газа, µ - молярная масса газа. Если система представляет смесь из нескольких газов, то количество вещества системы

или

,

где - соответственно количество вещества, число молекул, масса, молярная масса i -ой компоненты смеси.

2. Уравнение Менделеева - Клапейрона (уравнение состояния идеального газа):

,

где m - масса газа, µ - молярная масса газа, R - универсальная газовая постоянная, v - количество вещества, Т - термодинамическая температура Кельвина.

3. Опытные газовые законы, являющиеся частными случаями уравнения Менделеева - Клайперона для изопроцессов:

а) закон Бойля-Мариотта (изотермический процесс: Т = сonst, m = сonst):

,

или для двух состояний газа:

,

где P₁ и V₁ - давление и объем газа в начальном состоянии, Р₂ и V₂ - те же величины в конечном состоянии.

б) закон Гей-Люссака (изобарический процесс Р = сonst, m = сonst )

или для двух состояний:

,

где T₁ и V₁ температура и обьем газа в начальном состоянии, Т₂ и V₂ - те же величины в конечном состоянии.

в) закон Шарля (изохорический процесс V = сonst, m = сonst)

,

или для двух состояний

,

где P₁ и T₁ - давление и температура газа в начальном состоянии, Р₂ и Т₂ - те же величины в конечном состоянии.

г) объединенный газовый закон (m = сonst)

где - давление, объем и температура газа в начальном состоянии Р₂, V₂, T₂ - те же величины в конечном состоянии.

4. Закон Дальтона, определяющий давление смеси газов:

,

где P_i - парциальное давление компонента смеси, n - число компонентов смеси.

5. Молярная масса смеси газов

,

где m_i - масса i-го компонента смеси, - количество вещества i-го компонента смеси, n - число компонентов смеси.

6. Массовая доля i-го компонента смеси газов (в долях единицы или в процентах):

,

где m - масса смеси.

7. Концентрация молекул (число молекул в единице объема)

,

где N - число молекул, содержащихся в данной системе, ρ - плотность вещества.

Формула справедлива не только для газов, но и для любого состояния вещества.

8. Основное уравнение кинетической теории газов:

,

где <w_n> - средняя кинетическая энергия поступательного движения молекулы.

9. Средняя кинетическая энергия поступательного движения молекулы

,

где k - постоянная Больцмана.

10. Средняя полная кинетическая энергия молекулы:

,

где i - число степеней свободы молекулы.

11. Зависимость давления газа от концентрации молекул и от температуры:

.

12. Скорости молекул:

- средняя арифметическая,

- средняя квадратичная,

- наиболее вероятная,

где - масса одной молекулы.

13. Относительная скорость молекулы:

,

где - скорость данной молекулы.

14. Удельные теплоемкости газов при постоянном объеме c_V и при постоянном давлении с_P:

.

15. Связь между удельной (с) и молярной (С) теплоемкостями:

.

16. Уравнение Роберта Майера:

.

17. Внутренняя энергия идеального газа

.

18. Первое начало термодинамики:

Q = ∆U + A,

где Q - теплота, сообщенная системе (газу), ΔU - изменение внутренней энергии системы. А - работа, совершенная системой против внешних сил.

19. Работа расширения газа:

в общем случае ,

при изобарическом процессе ,

при изотермическом процессе ,

при адиабатическом процессе

или

,

где - показатель адиабаты.

20. Уравнения Пуассона, связывающие параметры идеального газа при адиабатическом процессе:

21. Термический КПД цикла:

,

где - теплота, полученная рабочим телом от нагревателя, Q₂ - теплота, переданная рабочим телом охладителю.

22. Термический КПД цикла Карно:

,

где T₁ и Т₂ - термодинамические температуры нагревателя и температуры охладителя.

23. Коэффициент поверхностного натяжении:

,

где F - сила поверхностного натяжения, действующая на контур длиной , ограничивающий поверхность жидкости, ∆Е - изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади ∆S поверхности этой пленки.

24. Формула Лапласа, выражающая давление Р, создаваемое сферической поверхностью жидкости:

,

где R - радиус сферической поверхности.

25. Высота подъема жидкости в капиллярной трубке:

,

где θ - краевой угол (θ = 0 при полном смачивании стенки трубки жидкостью, θ = π при полном несмачивании), R = радиус канала трубки, 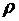- плотность жидкости, g - ускорение свободного падения.

27. Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями:

,

где d - расстояние между плоскостями.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Определить число N молекул, содержащихся в объеме V = 1 мм³ воды, массу молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул.

Решение: Число N молекул, содержащихся в некоторой массе равно произведению числа Авогадро на количество вещества :

так как количество вещества:

μ - молярная масса, то

Выразив в этой формуле массу, как произведение плотности на объем V, получим

. (1)

Подставим в формулу (1) следующие значения величин: 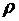= 10³ кг/м³,

V = 1 мм³ = м , μ = кг/моль, = моль и произведем вычисления:

молекул = 3,34 10¹⁹молекул.

Массу , одной молекулы можно найти делением молярной массы на число Авогадро:

Подставим сюда числовые значения μ и и найдем массу молекулы воды:

кг = кг.

Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка) , где d - диаметр молекулы воды. Отсюда

(2)

Объем найдем, разделив молярный объем на число молекул в моле, т.е. на число Авогадро :

Подставим полученное выражение в формулу (2):

Входящий в эту формулу молярный объем определяется выражением , тогда искомый диаметр молекулы:

(3)

Проверим, дает ли правая часть выражения (3) единицу длины:

Теперь подставим числовые значения физических величин в формулу (3) и произведем вычисления:

Пример 2. В баллоне объемом V = 10 л находится гелий под давлением Р 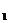= 1 МПа и при температуре Т 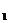= 300 К. После того, как из баллона было взято m = 10 г гелия, температура в баллоне понизилась до Т = 290 К. Определить давление Р гелия, оставшегося в баллоне.

Решение: Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа:

(1)

где - масса гелия в баллоне в конечном состоянии, μ - молярная масса гелия, R - универсальная газовая постоянная. Из уравнения (1) выразим искомое давление Р .

(2)

Массу гелия m₂ выразим через массу m₁, соответствующую начальному состоянию и массу m гелия, взятого из баллона:

(3)

Массу гелия m найдем также из уравнения Менделеева-Клапейрона, применив его к начальному состоянию

(4)

Подставляя в выражение (3) массу из формулы (4), а затем полученное выражение в формулу (2), найдем:

После преобразования и сокращения находим:

(5)

Левая часть расчётной формулы (5) выражает давление, имеет размерность . Проверим размерность правой части. Размерность первого слагаемого не вызывает сомнения, т.к. отношение температур – величина безразмерная. Размерность второго слагаемого:

что совпадает с размерностью давления.

Убедившись в том, что размерность правой и левой частей формулы (5) одинаковы, выразим величины,входящие в эту формулу, в единицах СИ и произведем вычисления:

P₁ = 1 МПа =10⁶ Па, , ,

R = 8,31 Дж/(мольК), T₁ = 300 К, T₂ = 290 К,

V = 10 л = 10^{-2 м3},

Пример 3.Баллон содержит = 80 г кислорода и = 320 г аргона. Давление смеси Р = 1 МПа, температура Т = 300 К. Принимая данные газа за идеальные, определить объем V баллона.

Решение. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих всостав смеси. Парциальным давлением газа называется давление, которое производил бы этот газ, если бы только он один находился в сосуде, занятым смесью. По уравнению Менделеева-Клапейрона, парциальные давления кислорода и аргона выражается формулами:

Следовательно, по закону Дальтона давление смеси газов

откуда объем баллона:

Выразим в единицах СИ числовые значения величин, входящих в эту формулу m₁ = 80 г = 0,8 кг, , m₂ = 330 г = 0,33 кг, , m₂ = 40 10^-3 кг/моль, P₁ = 1 МПа = 10⁶ Па, R = 8,31 Дж/(мольК), подставим числовые значения в формулу и произведем вычисления:

Пример 4. Найти среднюю кинетическую энергию вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию вращательного движения всех молекул кислорода массой m = 4 г.

Решение: Известно, что на каждую степень свободы молекулы газа приходится одинаковая средняя энергия , где - постоянная Больцмана, Т - абсолютная температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода двухатомная) соответствует две степени свободы, то средняя энергия вращательного движения молекулы кислорода выразится формулой:

(1)

Подставив в формулу (1) значение и T = 350 К получим . Кинетическая энергия вращательного движения всех молекул газа определяется равенством:

(2)

Число всех молекул газа можно вычислить по формуле:

(3)

где число Авогадро, - количество вещества. Если учесть, что количество вещества , где - масса газа, μ - молярная масса газа, то формула (3) примет вид:

Подставив это выражение в формулу (2) получим:

(4)

Выразим величины, входящие в эту формулу, в единицах СИ:

, , , . Подставив эти значения в формулу (4), найдем:

Пример 5. Вычислить удельные теплоемкости при постоянном объеме и при постоянном давлении неона и водорода, принимая эти газы за идеальные.

Решение: Удельные теплоемкости идеальных газов выражаются формулами

(1)

(2)

где - число степеней свободы молекул газа, - молярная масса. Для неона (одноатомный газ) , кг/моль (см. справочную таблицу). Вычисляя по формулам (1) и (2), получим:

Для водорода (двухатомный газ) , кг/моль. Вычисляя по тем же формулам, получим:

Пример 6. Вычислить удельные теплоемкости и смеси неона и водорода, если массовая доля неона = 80%, массовая доля водорода = 20%. Значение удельных теплоемкостей газов взять из предыдущего примера.

Решение: Удельную теплоемкость смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на , выразим двумя способами.

(1)

(2)

где - удельная теплоемкость неона, - удельная теплоемкость водорода. Приравняв правые части (1) и (2) и разделив обе части полученного равенства на . получим:

отсюда

(3)

или

(4)

где и - массовые доли неона и водорода в смеси. Подставив в формулу (4) числовые значения величин, найдем:

Рассуждая таким же образом, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:

(5)

Подставим в формулу (5) числовые значения величин:

Пример 7. Кислород массой m = 2 кг занимает объем равный V = 1 м³ и находится под давлением P 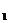= 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V₂= 3 м³, а затем при постоянном объеме до давления Р 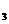= 0,5 МПа. Найти изменение внутренней энергии газа, совершенную им работу А и теплоту Q , переданную газу. Построить график процесса.

Решение: Изменение внутренней энергии газа выражается формулой:

(1)

где i - число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5), μ - молярная масса. Начальную и конечную температуру газа найдем из уравнения Клапейрона-Менделеева:

(2)

Выпишем заданные величины в единицах системы СИ: , кг/моль, = 8,31 Дж/моль К, V 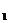= 1 м , V₂ = V₃ = 3 м ³, P 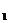= P₂ = 0,2 МПа = 2 10⁵ Па, Р = 0,5 МПа = 5 10⁵ Па. Подставляя эти значения в выражение (2) и выполняя арифметические действия, получим:

;

; .

Подставляя в выражение (1) числовые значения величин, входящих в него и выполняя арифметические действия, находим:

Работа расширения газа при постоянном давлении выражается формулой:

Подставим числовые значения величин, получим:

.

Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е. . Следовательно, полная работа, совершенная газом, равна

= Дж.

Согласнопервому началу термодинамики теплота Q, переданная газу, равна сумме изменения внутренней энергии и работы A: , следовательно .

Пример 8. Тепловая машина работает по обратному циклу Карно. Температура нагревателя T = 500 К. Определить термический КПД цикла и температуру Т₂ охладителя тепловой машины, если за счет каждого килоджоуля теплоты, полученной от нагревателя, машина совершает работу А = 350 Дж.

Решение: Термический КПД тепловой машины, называемый также коэффициентом использованной теплоты, показывает, какая доля теплоты, полученной от нагревателя, превращается в механическую работу. Термический КПД выражается формулой:

где Q - теплота, полученная от нагревателя, А - работа, совершаемая рабочим телом тепловой машины. Подставив числовые значения в эту формулу, получим

Зная КПД цикла, можно по формуле определить температуру охладителя Т₂:

Подставив в эту формулу полученное значение КПД и температуры T нагревателя, получим:

Пример 9. Найти добавочное давление внутри мыльного пузыря диаметром d = 10 см. Какую работу нужно совершить, чтобы выдуть этот пузырь?

Решение: Пленка мыльного пузыря имеет две сферические поверхности - внешнюю и внутреннюю. Обе поверхности оказывают давление на воздух, заключенный внутри пузыря. Так как толщина пленки чрезвычайно мала, то диаметры обеих поверхностей практически одинаковы. Поэтому добавочное давление, где - . где радиус пузыря. Так как , то . Коэффициент поверхностного натяжения мыльной воды 40 мН/м (см. справочную табл.) диаметр пузыря = 10 см = 0,1 м.

Работа, которую нужно совершить, чтобы, растягивая пленку, увеличить её поверхность на , выражается формулой

В данном случае - общая площадь двух сферических поверхностей пленки, затягивающей отверстие трубки до выдувания пузыря, пренебрегая , получим

Подставив числовые значения величин, получим:

.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

200. Определить количество вещества v и число N молекул кислорода массой m = 0,5 кг.

201. Сколько атомов содержится в ртути 1) количеством вещества = 0.2 моль, 2) массой m = 1 г.

202. Вода при температуре занимает объем . Определить количество вещества и число N молекул воды.

203. Найти молярную массу и массу одной молекулы поваренной соли.

204. Определить массу m одной молекулы поваренной соли.

205. Определить концентрацию n молекул кислорода, находящего в сосуде объемом V = 2 л. Количество v вещества кислорода равно 0,2 моль.

206. Определить количество вещества водорода, заполняющего сосуд объемом V = 3 л, если концентрация молекул газа в сосуде .

207. Газ в колбе емкостью , находящейся при температуре , разрежен до давления 550 мм. рт. ст. Определить, сколько молекул содержится в колбе и число молей газа.

208. Из сосуда испарилось за 10 суток 100 г воды. Сколько в среднем молекул вылетало из сосуда за одну секунду?

209. Сколько молей и какое количество молекул газа находится в баллоне объемом 2 литра, если температура газа 47°C, а давление ?

210. В сосуде объемом 0,7 м³ находится смесь 8 кг водорода и 4 кг кислорода при температуре 7°C. Определить давление и молярную массу смеси газа.

211. В сосуде объемом 200 литров содержится азот при температуре 2°C. Часть азота израсходовали и давление снизилось на Па. Сколько израсходовано газа?

212. Азот находится под давлением Па и занимает объем 2,8 л. Масса азота 56 г. На сколько изменится температура газа, если его объем уменьшится в два раза, а давление увеличится до Па?

213. Каково будет давление воздуха, если 5 л его сжаты до объема 1,5 л при неизменной температуре? Начальное давление воздуха 690 мм. рт. ст. Постройте по точкам график процесса в координатах P, V.

214. В баллоне при давлении Па содержится газ при температуре 47°C. Когда 1/3 массы газа была выпущена из баллона, температура снизилась на 20°C. Как изменилось давление?

215. В сосуде объемом V = 40 л находится кислород при температуре T = 300 K. Когда часть кислорода израсходовали, давление в баллоне понизилось на = 100 кПа. Определить массу израсходованного кислорода, если его температура не изменилась.

216. Два сосуда одинакового объема содержат кислород. В одном сосуде давление и температура , в другом , . Сосуды соединили трубой и охладили находящийся в них кислород до . Определить установившееся в сосудах давление.

217. Смесь кислорода и азота находится в сосуде под давлением P = 1,2 МПа. Определить парциальное давление и газов, если массовая доля кислорода в смеси составляет 20%.

218. Смесь водорода и азота общей массой m = 290 г при температуре T = 600 К и давлении P = 2,46 МПа занимает объем V = 30 л. Определить массу водорода и массу азота.

219. Смесь азота с массовой долей 87,5% и водорода с массовой долей 12,5% находится в сосуде объемом V = 20 л при температуре T = 560 К. Определить давление P смеси, если масса смеси равна 8 г.

220. Определить суммарную кинетическую энергию поступательного движения всех молекул газа, находящегося в сосуде объемом V = 3 л под давлением P = 540 кПа.

221. Количество вещества гелия v = 1,5 моль, температура T = 120 К. Определить суммарную кинетическую энергию поступательного движения всех молекул этого газа.

222. Определить среднюю кинетическую энергию <w> одной молекулы водяного пара при температуре T = 500 К.

223. Определить среднюю квадратную скорость < > молекул газа, заключенного в сосуде объемом V = 2 л под давлением P = 200 кПа. Масса газа m = 0,3 г.

224. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса m каждой пылинки равна г. Газ находится при температуре T = 400 К. Определить средние квадратичные скорости < >, а так же средние кинетические энергии поступательного движения молекул азота и пылинки.

225. Вычислить кинетические энергии поступательного, вращательного движений и полную кинетическую энергию молекул аргона, кислорода и паров воды при температуре 27°C, а также средние квадратичные скорости молекул.

226. Определить полную энергию молекул азота, который находится в баллоне объемом V = 100 л при давлении .

227. При температуре 37°C движется взвешенные в воздухе мельчайшие пылинки массой 10^{-12 кг} каждая. Определить среднюю квадратичную, среднюю арифметическую и наиболее вероятную скорости пылинок.

228. Кислород находится под давлением 1,2 атм, молекулы имеют среднюю квадратичную скорость 500 м/с. Определить среднюю длину свободного пробега молекул.

229. Найти среднее число столкновений <z> в единицу времени и длину свободного пробега <l> молекулы гелия, если газ находится под давлением P = 2 кПа при температуре T = 200 К.

230. Определить показатель адиабаты азота, который при температуре T = 350 К и давлении P = 0,4 МПа занимает объем V = 300 л и имеет теплоемкость C = 857 Дж/К.

231. В сосуде объемом V = 6 л находится при нормальных условиях двухатомный газ. Определить теплоемкость этого газа при постоянном объеме.

232. Определить молярные теплоемкости газа, если его удельные теплоемкости c_V = 10,4 кДж/кгК и c_p = 14,6 кДж/кгК.

233. Найти удельные , и молярные и теплоемкости азота и гелия.

234. Вычислить удельные теплоемкости газа, зная, что его молярная масса кг/моль и отношение теплоемкостей =1,67.

235. Трехатомный газ под давлением P = 240 кПа и температуре t = 20°C занимает объем V = 10 л. Определить теплоемкость этого газа при постоянном давлении.

236. Удельная теплоемкость газа . Отношение = 1,4. Определить молярную массу газа.

237. Определить относительную молекулярную массу и молярную массу газа, если его разность удельных теплоемкостей показатель .

238. Смесь двух газов состоит из гелия массой m₁ = 5 г и водорода массой m₂ = 2 г. Найти отношение теплоемкостей этой смеси.

239. Относительная молярная масса M_r = 30, показатель адиабаты g = 1,40. Вычислить удельные теплоемкости и этого газа.

240. Определить изменение внутренней энергии 10 кг водорода при изобарическом расширении, если в процессе нагревания температура повысилась на 100°С.

241. В баллоне емкостью 10 дм³ содержится кислород при температуре 30°C и под давлением 10⁷ Па. При нагревании кислород получил Дж теплоты. Определить температуру и давление кислорода после нагревания.

242. Водород занимает объем V = 1 м³ при давлении . Газ нагрели при постоянном давлении . Определить изменение внутренней энергии газа и теплоту, сообщенную газу.

243. Кислород при неизменном давлении P = 100 кПа нагревается. Его объем увеличивается от V₁ = 1 м³ до V₂ = 2 м³. Определить изменение внутренней энергии кислорода.

244. В цилиндре под поршнем находится азот, имеющий массу m = 5 кг и занимающий объем V₁ = 8 м³ при температуре . После нагревания объем газа V₂ = 27 м³, температура осталась неизменной. Найти работу расширения газа.

245. Один моль гелия изобарически расширяется от объема = 5 л до объема при давлении . Определить изменение внутренней энергии тела в этом процессе.

246. Один грамм кислорода ( ) нагревается от до при P = const. Определить изменение внутренней энергии.

247. Два грамма азота нагреваются от до при V = const. Определить изменение внутренней энергии.

248. Один грамм кислорода нагревается от до при = 0. Определить изменение внутренней энергии.

249. Азот занимает объем и находится под давлением P₁ = 10⁵ Па. Газ нагревают при постоянном объеме до давления P₂ = 5∙10⁵ Па. Масса азота m = 3 кг. Определить из<