Волновое уравнение для электромагнитных волн
Факт получения волнового уравнения из уравнений Максвелла означает само существование электромагнитных волн.
Для однородной нейтральной ( 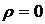 ) и непроводящей (
) и непроводящей ( 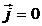 ) среды при постоянных
) среды при постоянных 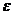 и
и 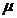 запишем:
запишем:
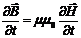 ,
, 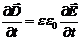 ,
,
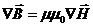 ,
, 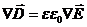 .
.
С учетом этих выражений перепишем уравнения Максвелла в дифференциальном виде следующим образом:
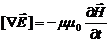 , (3)
, (3)
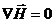 , (4)
, (4)
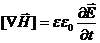 , (5)
, (5)
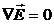 . (6)
. (6)
Возьмем ротор от обеих частей уравнения (3):
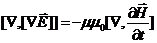 . (7)
. (7)
В правой части поменяем местами последовательности дифференцирования:
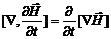 .
.
Подставим в (7) и используем (5):
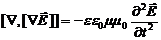 . (8)
. (8)
Преобразуем левую часть: 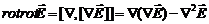 . Первое слагаемое =0 (см.(6)), а
. Первое слагаемое =0 (см.(6)), а 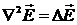 . Тогда
. Тогда
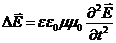 .
.
или
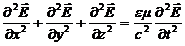 . (9)
. (9)
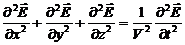 . (9/ )
. (9/ )
Аналогично для 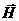 :
:
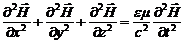 . (10)
. (10)
Уравнения (7) и (8) указывают, сто электромагнитные поля могут существовать в виде электромагнитных волн с фазовой скоростью 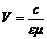 .
.
21Плотность энергии электромагнитного поля равна сумме плотностей для электрического и магнитного полей (при отсутствии сегнетоэлектриков и ферромагнетиков):
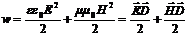 . (11)
. (11)
Учитывая (2), получим, что 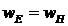 для каждого момента времени, тогда
для каждого момента времени, тогда
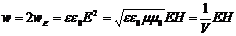 .Пойнтинг ввел понятие вектора плотности потока энергии:
.Пойнтинг ввел понятие вектора плотности потока энергии:
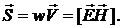 (12)
(12)
Поток Ф электромагнитной энергии равен
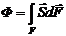 .
.
Давление и импульс
Давление электромагнитной волны на тело, на которое она падает возникает в результате воздействия магнитного поля волны на электрические токи, возбуждаемые электрическим полей той же волны.
Пусть электромагнитная волна падает на поглощающее тело (среду), т.е. в нем возникает джоулево тепло с объемной плотностью σЕ2, т.е. 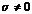 и поглощающая среда обладает проводимостью. В такой среде электрическое поле волны возбуждает электрический ток с плотностью
и поглощающая среда обладает проводимостью. В такой среде электрическое поле волны возбуждает электрический ток с плотностью 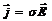 . Тогда на единицу объема среды действует амперова сила
. Тогда на единицу объема среды действует амперова сила 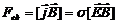 в направлении волны. Эта сила и вызывает давление электромагнитной волны. Если нет поглощения, σ = 0 и давления нет. При полном отражении волны давление возрастает вдвое.
в направлении волны. Эта сила и вызывает давление электромагнитной волны. Если нет поглощения, σ = 0 и давления нет. При полном отражении волны давление возрастает вдвое.
Давление равно: 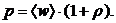 (13)
(13)
Плотность импульса равна 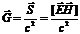 , что аналогично выражению
, что аналогично выражению 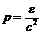 для импульса фотона.
для импульса фотона.
Энергией эл/магн – сумма эл и магн полей 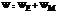
Объемная плотность энергии эл/магн поля: 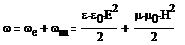
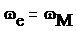
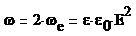
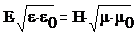
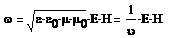
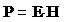
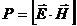 - вектор Умова- Пойтинга. Он направлен в сторону распространения эл/магн волны, а его модуль равен энергии, переносимой эл/магн волной за единицу времени сквозь единичную площадку, перпендикулярно направлению распространению волны.
- вектор Умова- Пойтинга. Он направлен в сторону распространения эл/магн волны, а его модуль равен энергии, переносимой эл/магн волной за единицу времени сквозь единичную площадку, перпендикулярно направлению распространению волны.
22 Электрический диполь- система из двух равных по величине, но противоположных по знаку, зарядов, разделенных некоторым расстоянием 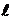 .
.
Если он колеблется, то излучает электромагнитные волны.
Изменение его момента со временем:
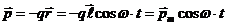 . (14)
. (14)
Рассмотрим элементарный диполь. Для него 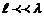 . В волновой зоне
. В волновой зоне 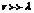 .
.
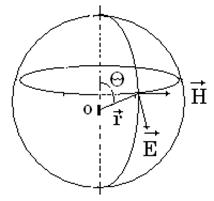
Для сферической волны
Em ~ Hm ~ 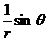 .
.
Следовательно, интенсивность волны
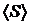 ~
~ 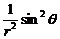
обратно пропорциональна квадрату расстояния от излучателя и зависит от угла θ. Диаграмма излучения диполя имеет вид (рис.3).
Рис.2
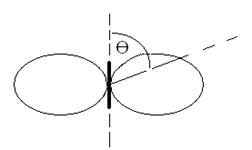
Рис. 3
Мощность излучения N ~ 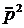 . Из (14)
. Из (14) 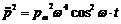 . Тогда
. Тогда
N ~ 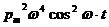 . (15)
. (15)
Усредним по времени
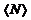 ~
~ 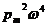 . (16)
. (16)
Из (14):
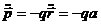 ,
,
где а – ускорение колеблющегося заряда.
Тогда мощность
N ~ q2 a2.
Интерференция световых волн
Пусть в одном направлении распространяются 2 световые волны:
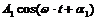 и
и 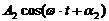
Тогда
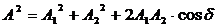 ,
,
где 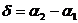 .
.
Если 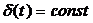 , то волны являются когерентными. Когерентными называются волны, у которых
, то волны являются когерентными. Когерентными называются волны, у которых 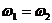 и постоянна во времени разность фаз.
и постоянна во времени разность фаз.
Для некогерентных волн δ непрерывно изменяется и ее среднее по времени значение = 0, поэтому
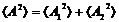 или
или 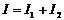 .
.
Для когерентных волн

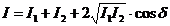 . (1)
. (1)
Явление перераспределения светового потока в пространстве, в результате чего в одних местах возникают максимумы интенсивности, а в других - минимумы, называется интерференцией.
Пример: Пусть 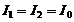 . Из (1) следует:
. Из (1) следует: 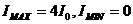 .Все естественные источники света некогерентны. Объяснение: Излучение тел состоит из волн, испускаемых многими атомами. Каждый атом излучает цуг волн продолжительностью
.Все естественные источники света некогерентны. Объяснение: Излучение тел состоит из волн, испускаемых многими атомами. Каждый атом излучает цуг волн продолжительностью 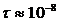 с и протяженностью
с и протяженностью 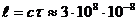 = 3 (м). Через τ излучение одной группы атомов сменяется излучением другой группы. Фазы разных цугов даже от одних атомов между собой не связаны, т.е. меняются случайным образом, так что при усреднении
= 3 (м). Через τ излучение одной группы атомов сменяется излучением другой группы. Фазы разных цугов даже от одних атомов между собой не связаны, т.е. меняются случайным образом, так что при усреднении 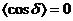 .
.
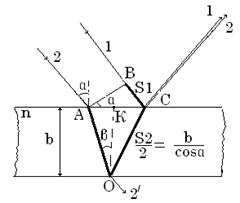
Как же в таком случае можно вообще наблюдать интерференцию? Проблема решается просто! Нужно путем отражений или преломлений разделить одну волны на 2 или более волн, которые после прохождения разных оптических длин путей следует вновь наложить друг на друга. Тогда наблюдается интерференция.
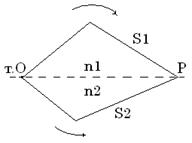
Разделим в т.О (рис.2) волну на две когерентные. В т.О фаза равна 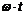 ,
,
в т. Р фаза 1-й волны: 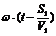 , a
, a
2-й волны: 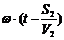 . Тогда разность фаз двух колебаний в точке наблюдения Р будет равна:
. Тогда разность фаз двух колебаний в точке наблюдения Р будет равна:
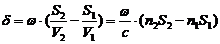 .
.
Рис. 2 Заменим 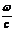 на
на 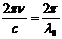 , тогда получим:
, тогда получим:
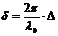 , (2)
, (2)
где
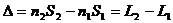 (3) - оптическая разность хода.
(3) - оптическая разность хода.
Если
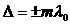 , (4)
, (4)
где 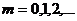 , то δ является кратной 2π и колебания, возбуждаемые в т.Р обеими волнами, будут происходить с одинаковой фазой и усиливают друг друга , т.е. (4) выражает условие максимума..
, то δ является кратной 2π и колебания, возбуждаемые в т.Р обеими волнами, будут происходить с одинаковой фазой и усиливают друг друга , т.е. (4) выражает условие максимума..
Условие минимума:
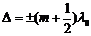 (5)
(5)
при 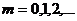 , т.е. на разности хода укладывается нечетное число полуволн в вакууме и колебания в т.Р обеих волн находятся в противофазе.
, т.е. на разности хода укладывается нечетное число полуволн в вакууме и колебания в т.Р обеих волн находятся в противофазе.
Под когерентностью подразумевается согласованное протекание колебательных или волновых процессов. При этом степень согласованности может быть различной.
Различают временную и пространственную когерентность.
Временная когерентность определяется разбросом частот Δω или разбросом значений модуля волнового вектора k, так как
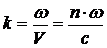 .
.
Пространственная же связана с разбросом направлений вектора 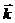 .
.
 При рассмотрении временной когерентности большую роль играет время срабатывания прибора tприб. Если за tприб cosδ принимает все значения от -1 до +1, то
При рассмотрении временной когерентности большую роль играет время срабатывания прибора tприб. Если за tприб cosδ принимает все значения от -1 до +1, то 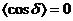 ; если за tприб
; если за tприб 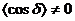 , то прибор фиксирует интерференцию и волны когерентны. Вывод: Когерентность – понятие относительное. Волны, когерентные при наблюдении прибором с малым tприб , могут быть некогерентными при приборе с большим tприб.
, то прибор фиксирует интерференцию и волны когерентны. Вывод: Когерентность – понятие относительное. Волны, когерентные при наблюдении прибором с малым tприб , могут быть некогерентными при приборе с большим tприб.
Для характеристики когерентных свойств волн вводится понятие времени когерентности 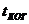 . Это – время, за которое изменение фазы волны достигает значения ~π. Теперь можно ввести
. Это – время, за которое изменение фазы волны достигает значения ~π. Теперь можно ввести
критерий когерентности: tприб « 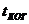 . (6)
. (6)
Длина когерентности(длина цуга) - 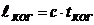 . (7)
. (7)
Это – расстояние, на котором изменение фазы волны достигает значения ~π.
Для получения интерференционной картины путем деления световой волны на две необходимо, чтобы 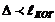 . Это требование ограничивает наблюдаемое число интерференционных полос. Расчеты дают следующие соотношения:
. Это требование ограничивает наблюдаемое число интерференционных полос. Расчеты дают следующие соотношения:
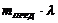 ~
~ 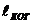 ~
~ 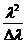 . (8)
. (8)
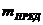 ~
~ 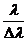 . (9)
. (9)
При рассмотрении пространственной когерентности критерий записывается в виде:
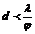 , (10)
, (10)
где φ - угловой размер источника, d – его линейный размер.
 При смещении вдоль волновой поверхности, излучаемой источником, расстояние, на котором фаза меняется не более чем на π, называется длиной пространственной когерентности или радиусом когерентности:
При смещении вдоль волновой поверхности, излучаемой источником, расстояние, на котором фаза меняется не более чем на π, называется длиной пространственной когерентности или радиусом когерентности:
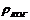 ~
~  . (11)
. (11)
Для солнечных лучей (φ ~ 0,01 рад, λ ~ 0,5 мкм. Тогда 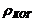 = 0,05 мм.
= 0,05 мм.
