Законы сохранения энергии при комптоновском упругом рассеянии.

Закон сохранения импульса имеет вид:

,

где 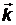и – волновые векторы падающего и рассеянного фотонов (модуль волнового вектора равен 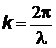). Графическая иллюстрация закона сохранения импульса приведена на Рис. 9. Закон сохранения энергии записывается в виде:

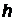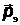(используется релятивистская формула, т.к. энергия падающего кванта сравнима в энергией покоя электрона). Здесь –постоянная Планка, с – скорость света, – масса электрона, – импульс электрона, 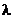и 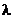¢ – длины падающей и рассеянной волн.

Рис.9 Графическая иллюстрация закона сохранения импульса в эффекте Комптона

В эффекте Комптона участвуют только свободные электроны, которые слабо связаны с атомами. Если же энергия связи электрона больше энергии фотона, то такой электрон не будет свободным и эффект Комптона не возникает. В этом случае фотон взаимодействует с жестко связанной системой электрон – ядро и «отскакивает» от нее, практически не изменяя своей энергии и длины волны. В реальном веществе фотоны сталкиваются как со свободными, так и с сильно связанными электронами, поэтому и возникают оба компонента рассеяния с длинами волн 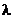и ¢.

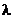Эффект Комптона не может происходить под действием квантов видимого света (с длинами волн 400 – 700 нм), поскольку их энергия составляет 3 – 1,8 эВ соответственно, что на 5 порядков меньше энергии покоя электрона – 511000 эВ.

Кинетическая энергия электрона отдачи: , где – энергия падающего фотона и – энергия рассеянного фотона.

Соотношение между энергией падающего и рассеянного фотонов при комптоновском рассеянии:

, откуда , где = 0,511 МэВ – энергия покоя электрона.

Примеры решения задач

Задача 1.В результате эффекта Комптона фотон при соударении с электро-ном был рассеян на угол 90°. Энергия рассеянного фотона равна 0,4 МэВ. Опре-делите энергию фотона 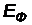до рассеяния.

Решение.Выразим в формуле Комптона длины волн и 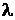через энергии и 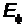соответствующих фотонов, воспользовавшись соотношением , , откуда

= 1,85 Мэв,

где = 0,51 МэВ, 1 МэВ = 1,6·10^-13 Дж.

Задача 2. Гамма-фотон с длиной волны 1,2 пм в результате комптоновского рассеяния на свободном электроне отклонился от первоначального направления на угол 60°. Определите кинетическую энергию и импульс электрона отдачи. До столкновения электрон покоился.

Решение.Из закона сохранения энергии кинетическая энергия электрона отдачи равна , где и – энергия падающего и рассеянного фотонов.

Выражая энергию падающего и рассеянного фотона через его длину волны и используя формулу изменения длины волны фотона при комптоновском рассеянии, получим: .

Для кинетической энергии электрона находим

Дж. = 0,521 МэВ.

пм – комптоновская длина волны электрона. Кинетическая энергия электрона сравнима с его энергией покоя , поэтому его импульс найдем по релятивистской формуле

= 4,8·10^-22кг·м/c.

Задача 3.Фотон с импульсом 5,44×10^–22 кг×м/с в результате эффекта Компто-

на был рассеян на свободном электроне на угол 30°. Найти импульс рассеянного фотона.

Решение.Выражая импульс фотона через его длину волны и используя формулу изменения длины волны при эффекте Комптона получим:

, или ,

откуда = 4,3×10^–22 кг×м/с.