Дуализм свойств электромагнитного излучения.

В одних явлениях (интерференция, дифракция и др.) свет проявляет свои вол-

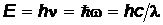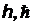новые свойства, а при тепловом излучении и при поглощении в фотоэффекте свет ведет себя как поток частиц (названных фотонами) с энергией: , где – постоянные Планка, w– циклическая частота электромагнитного излучения, n – частота электромагнитного излучения, с – скорость света в вакууме, 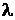–длина волны электромагнитного излучения.

Фотон имеет нулевую массу покоя, движется со скоростью света и его импульс p равен:

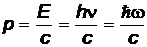или ,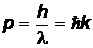

где 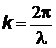– волновое число, 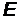– энергия фотона, направление импульса фотона 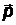совпадает с направлением волнового вектора : .

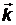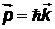Давление света

Свет оказывает давление на освещаемую поверхность. Рассмотрим монохроматический световой поток частоты ν, падающий по нормали на плоскую поверхность площадью S с коэффициентом отражения ρ. По закону сохранения импульса относительно оси z, нормальной к поверхности

,

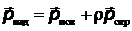где 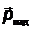- импульс падающего фотона с частотой ν ( 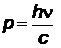), 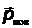- импульс, передаваемый фотоном поверхности, 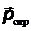- импульс отраженного фотона, ρ – коэффициент отражения. N фотонов передают поверхности импульс 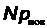. Число фотонов, падающих по нормали на поверхность за время Δt равно 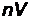, где n – число фотонов в единице объема, V – объем цилиндра площадью S и длиной сt, 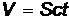. (Рис.7).

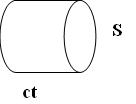
Рис.7

Импульс 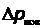, передаваемый поверхности световым потоком за время Δt, равен

,

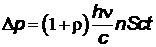а давление

,

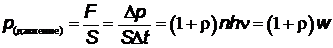где nhν – энергия фотонов в единичном объеме падающего светового потока, то есть плотность энергии w.

Примеры решения задач.

Задача 1.Определите, с какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона с длиной волны 1) 0,55 мкм,

2) 1 пм.

Решение.Чтобы определить, является ли электрон классической или релятивистской частицей, энергию фотона 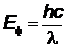следует сравнить с энергией покоя электрона 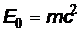. Вычислим соотношение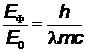

В первом случае получим 4,41·10^-6 , т.е. кинетическая энергия электрона много меньше его энергии покоя, и определяется по классической формуле: 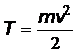. Тогда

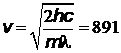м/с.

Во втором случае 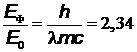, следовательно, кинетическая энергия электрона определяется релятивистской формулой:

.

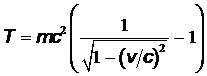Приравняв ее к энергии фотона 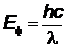, найдем

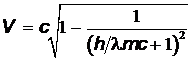= 2,87×10⁸ м/с.

Задача 2. Определите температуру, при которой средняя энергия молекул трехатомного газа равна энергии фотонов, соответствующих излучению с длиной волны 500 нм.

Решение. Средняя энергия молекулы 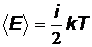,где 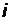- число степеней свободы, для трехатомного газа 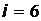. Энергия фотона .

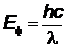Приравняв, эти энергии 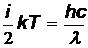, получим 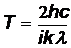= 9,6 кК.

Задача 3.Определите длину волны фотонов, импульс которого равен импульсу электрона, прошедшего разность потенциалов 10 В.

Решение. Кинетическая энергия электрона 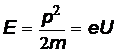, откуда его импульс 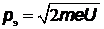. Приравняв его к импульсу фотона 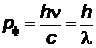, получим:

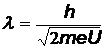= 388 пм.

Задача 4.Сколько фотонов испускает электрическая лампочка мощностью 25 Вт за время t = 1 с, если предположить, что вся потребляемая мощность идет на излучение монохроматического света с длиной волны 600 нм?

Решение.Энергия, потребляемая электрической лампочкой 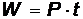равна энергии 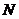испущенных фотонов 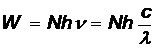, откуда число фотонов 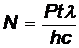= 7,54×10¹⁹.

Задача 5.Параллельный пучок света длиной волны 500 нм падает нормально на зачерненную поверхность, производя давление 10 мкПа. Определите концентрацию фотонов в пучке и число фотонов, падающих на поверхность площадью 1 м² за 1 с.

Решение.Концентрация 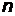фотонов в пучке может быть найдена из выраже-

ния для объемной плотности энергии :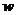

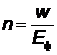, где 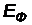- энергия одного фотона.

Из формулы, определяющей давление света, 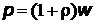, где r - коэффициент отражения, найдем

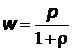, откуда .

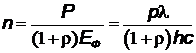Коэффициент отражения для зачерненной поверхности 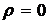, тогда

n = 2,52·10¹³м^-3. Число фотонов, падающих на поверхность единичной площади в единицу времени, выражается соотношением

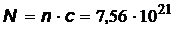м^-2·с^-1.

Эффект Комптона.

В 1922 году А. Комптон, исследуя рассеяние рентгеновского излучения различными веществами обнаружил, что в нем наряду с исходной длиной волны 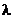появляется смещенная линия с длиной волны 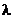¢ > 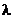(Рис.8).

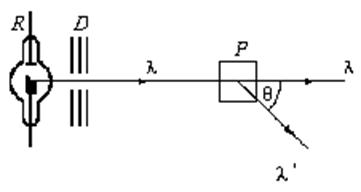
Рис.8 Схема установки по изучению эффекта Комптона

Это изменение длины волны получило название комптоновского смещения, а само явление эффекта Комптона. Комптоновское смещение 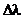не зависит от длины волны 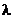и от природы рассеивающего вещества и определяется формулой:

,

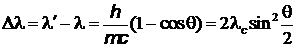где 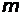– масса электрона или другой заряженной частицы, 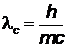- комптоновская длина волны этой частицы, l и l¢ - длины волн падающего и рассеянного излучения; q–угол рассеяния. Для электрона 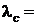2,42пм.

Все закономерности эффекта Комптона можно объяснить, если рассмотреть упругое столкновение рентгеновского кванта с покоящимся электроном, слабо связанным с атомом. Происходит процесс, напоминающий удар двух биллиардных шаров, когда один шар (рентгеновский квант) налетает на покоящийся шар (электрон) и в результате абсолютно упругого удара шары (рассеянный квант и электрон) разлетаются под некоторым углом. Налетающий квант с энергией 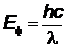передает часть своей энергии электрону, поэтому рассеянный квант имеет меньшую энергию и, следовательно, большую длину волны. Энергия рентгеновского кванта (десятки кэВ) на несколько порядков превосходит энергию связи электрона в атоме (десятки эВ), поэтому наиболее слабо связанные с атомом электроны внешних оболочек можно считать свободными и покоящимися.