Вопрос. Основы классической (электронной) теории электропроводности металлов. Вывод закона Ома в дифференциальной форме.

Вопрос. Объяснение закона Джоуля-Ленца в рамках классической теории электропроводности металлов. Объяснение наличия сопротивления проводников. Недостаточность классической электронной теории электропроводности.

1) К концу своего свободного пробега электрон достигает скорости:

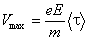
и энергии:

.

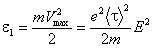Вся эта энергия, как уже отмечалось, при соударении с ионом передаётся кристаллической решётке, то есть преобразуется в тепло, которое идёт на нагревание металла. В единицу времени электрон претерпевает 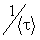соударений. Если учесть, что в единице объёма n электронов проводимости, то в единицу времени в единице объёма металла выделится такое количество теплоты:

Сопоставив этот результат с формулой (6.16) P_уд = lE², приходим к выводу, что электронная теория электропроводности металлов привела к закону Джоуля-Ленца в дифференциальной форме. Коэффициент пропорциональности, связывающий удельную тепловую мощность электрического тока P_уд с квадратом напряжённости электростатического поля — это по-прежнему удельная электропроводность металла:

.

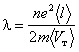2) Есть два проводника разного сечения. Проводники состоят из атомов и электронов - носителей тока. При приложении поля (напряжения) , возникает упорядоченное движение электронов - электрический ток. При этом часть электронов рассеивается на неоднородностях ионной решетки (примесях, дефектах, а также нарушениях структуры, связанных с тепловыми колебаниями ионов) . В проводнике большего сечения, количество электронов, которые беспрепятственно переместились по некоторому участку будет больше, а значит будет больше и ток. А согласно закону Ома R=U / I, он будет иметь меньшее сопротивление.

3) Как было показано выше, отношение 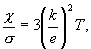Произведенные Лоренцем, уточненные расчеты с учетом классического распределения по скоростям привели к замене в теоретической формуле множителя 3 на 2 и к резкому увеличению расхождения теории с опытом. Второе затруднение классической электронной теории возникло при сопоставлении с опытом формул для теплоемкостей. Согласно электронной теории теплоемкость единицы объема электронного газа равна 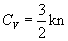, где n - концентрация свободных электронов. Теплоемкость, отнесенная к одному электрону, 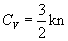. Рассмотрим один кг - атом одновалентного металла. Он состоит из 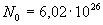ионов, колеблющихся около своих положений равновесия, и 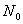свободных электронов. Колебательная теплоемкость твердого тела по закону Дюлонга и Пти равна 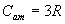, теплоемкость электронного газа

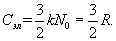
Следовательно, по электронной теории теплоемкость одновалентных металлов должна составлять 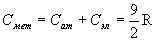. Однако опыт показывает, что теплоемкость металлов так же, как теплоемкость твердых диэлектриков, в соответствии с законом Дюлонга и Пти близка к 3R. Таким образом, обнаружилось неожиданное и непонятное явление практического отсутствия теплоемкости у электронного газа.

Третьим затруднением классической электронной теории металлов явилась невозможность правильно объяснить с ее помощью температурную зависимость сопротивления. Опыт показывает, что сопротивление металлических проводников линейно возрастает с температурой по закону

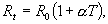
т.е. проводимость обратно пропорциональна абсолютной температуре в первой степени: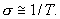

Согласно классической теории, проводимость обратно пропорциональна 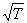. Наконец, возникли трудности при оценке средней длины свободного пробега электронов в металле. Для того чтобы, пользуясь формулой (18.3), получить такие значения удельной электрической проводимости металла, которые не расходились бы с опытными, приходится принимать среднюю длину свободного пробега электронов в сотни раз большей, чем период решетки металла. Иными словами, приходится предположить, что электрон проходит без соударений с ионами решетки сотни межузельных расстояний. Такое предположение непонятно в рамках классической электронной теории Друде -Лоренца.

Приведенные выше противоречия указывают на то, что классическая электронная теория, представляя электрон как материальную точку, подчиняющуюся законам классической механики, не учитывала некоторых специфических свойств самого электрона, которые еще не были известны к началу XX века. Эти свойства были установлены позднее при изучении строения атома, и в 1924 г. была создана новая, так называемая квантовая или волновая механика движения электронов.

Вопрос. Эффект Холла.

Одним из проявлений магнитной составляющей силы Лоренца в веществе служит эффект, обнаруженный в 1879 г. американским физиком Э.Г. Холлом (1855–1938). Эффект состоит в возникновении на боковых гранях проводника с током, помещенного в поперечное магнитное поле, разности потенциалов, пропорциональной величине тока I и индукции магнитного поля В.

Рассмотрим эффект, обусловленный действием лоренцевой силы 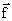на свободные заряды в проводнике. Представим себе проводник с током I в виде плоской ленты, расположенной в магнитном поле с индукцией 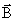, направленной от нас (рис. 2.19).

В случае изображенном на рис. 2.19, а, верхняя часть проводника будет заряжаться отрицательно, в случае 2.19, б – положительно.

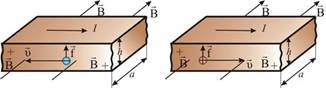
аб

Рис. 2.19

Это позволяет экспериментально определить знак носителя заряда в проводнике.

При равной концентрации носителей заряда обоих знаков возникает холловская разность потенциалов, если различна подвижность, т.е. дрейфовая скорость носителей заряда.

Подсчитаем величину холловской разности потенциалов (U_х).

Обозначим: E_x – напряженность электрического поля, обусловленного ЭДС Холла, h – толщина ленты проводника.

(2.10.1)

Перераспределение зарядов прекратится, когда сила qE_x уравновесит лоренцеву силу, т.е.

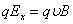или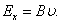

Плотность тока 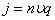,отсюда 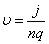.Тогда .

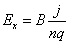Подставим E_x в (2.10.1) и найдем U_x:

,

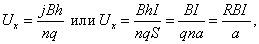(2.10.2)

где 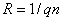– коэффициент Холла.

Исследования ЭДС Холла привели к удивительным выводам. Металлы могут обладать проводимостью р-типа (Zn, Cd – у них дырки более подвижные, чем электроны). Это металлы с чуть перекрывающимися знаками, т.е. полуметаллы.

Из формулы (2.10.2) можно найти число носителей заряда:

(2.10.3)

Итак, измерение холловской разности потенциалов позволяет определить:

· знак заряда и тип носителей;

· количество носителей.

Рис 2.20

На рисунке 2.20 показана установка для исследования магнитного поля длинного соленоида с помощью датчика Холла.

Ионизация газа

- это распад нейтральных атомов или молекул на положительные ионы и электроны путем отрыва электронов от атомов. Ионизация происходит при нагревании газа или воздействия излучений (УФ, рентген, радиоактивное) и объясняется распадом атомов и молекул при столкновениях на высоких скоростях.

Газовый разряд
- это эл.ток в ионизированных газах.
Носителями зарядов являются положительные ионы и электроны. Газовый разряд наблюдается в газоразрядных трубках (лампах) при воздействии электрического или магнитного поля.

Рекомбинация заряженных частиц

- газ перестает быть проводником, если ионизация прекращается, это происходит в следствие рекомбинации ( воссоединения противоположно заряженных частиц).

Существует самостоятельный и несамостоятельный газовый разряд.

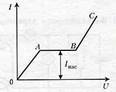
Несамостоятельный газовый разряд
- если действие ионизатора прекратить , то прекратится и разряд.

Когда разряд достигает насыщения - график становится горизонтальным. Здесь электропроводность газа вызвана лишь действием ионизатора.

Самостоятельный газовый разряд
- в этом случае газовый разряд продолжается и после прекращения действия внешнего ионизатора за счет ионов и электронов, возникших в результате ударной ионизации ( = ионизации эл. удара); возникает при увеличении разности потенциалов между электродами ( возникает электронная лавина).
Несамостоятельный газовый разряд может переходить в самостоятельный газовый разряд при Ua = Uзажигания.

7 Вопрос. Механизм возникновения самостоятельного газового разряда.

Чтобы разряд стал самостоятельным, каждый вырванный с катода электрон в результате цепочки взаимодействий должен вырвать с катода по крайней мере еще 1 электрон. Вспомним, что при ионизации атома электроном помимо свободного электрона возникает еще и ион, который движется под действием поля в противоположном электронам направлении – к катоду. В результате столкновения иона с катодом с последнего может быть эмитирован электрон (этот процесс называется вторичной электронной эмиссией). Сам механизм соответствует темному самостоятельному разряду. То есть при таких условиях не происходит генерация излучения. Падающий характер этого участка объясняется тем, что при больших токах нужны меньшие энергии электронов для сохранения самостоятельности разряда и, следовательно, меньшие ускоряющие поля.

Типы самостоятельного разряда. Техническое применение
1. Тлеющий разряд. Применяется в газосветных трубках, неоновых лампах, циф­ровых индикаторах, лампах дневного света, ртутных лампах низкого давления.
a. Несветящаяся часть, прилегающая к катоду, наз. темным катодным пространством, b. Светящийся столб газа, заполняющий остальную часть, наз. анодным положительным столбом. При определенных давлениях анодный столб распадается на отдельные слои, разделенные темными промежутками (страты). Причиной ионизации газа в тлеющем разряде является ударная ионизация и выбивание электронов из катода положительными ионами.
2. Дуговой разряд. Применяется в ртутных лампах высокого давления, источниках света, при сварке металлов, в электроплавильных печах, при электролизе расплавов, в электропечах.
3. Коронный разряд Высокая напряженность. Используют в электрофиль­трах для очистки газов от при­месей твердых частиц. Применяется в счетчиках заряженных частиц Гейгера-Мюллера. Громоотвод. Отрица­тельное явление: вызывает утеч­ку энергии на высоковольтных линиях.
4. Искровой разряд Высокое напряжение. Применяется при обработке металлов. Молния: U=108 В,I=105 А, продолжительность 10-6 с, диаметр канала 10 - 20 см.

Магнитное поле в веществе.

Природа ферромагнетизма

Возникновение магнитных свойств у ферромагнетиков связано с их доменным строением. Домены - это области самопроизвольной намагниченности, возникающие даже в отсутствие внешнего магнитного поля, в которых магнитные моменты атомов ориентированы параллельно.

Атомы или ионы приобретают магнитный момент, как правило, если они имеют нескомпенсированные спины электронов. Например в атомах железа на внутренней 3d-оболочке имеется четыре нескомпенсированных спина. Так как самопроизвольная намагниченность относится к внутриатомным явлениям, то ее природа может быть установлена только на основе квантово-механических понятий.

По Я.И.Френкелю и В.Гейзенбергу главную роль в возникновении ферромагнитного состояния играют силы обменного взаимодействия между атомами, имеющие квантовый характер и по происхождению являющиеся электростатическими.

Природа ферромагнетизма. Ферромагнетизм объясняется магнитными свойствами электронов. Электрон эквивалентен круговому току или вращающемуся заряженному телу и поэтому обладает собственным магнитным полем. В большинстве кристаллов магнитные поля электронов взаимно компенсируются благодаря попарной антипараллельной ориентации магнитных полей электронов. Лишь в некоторых кристаллах, например в кристаллах железа, возникают условия для параллельной ориентации собственных магнитных полей электронов. В результате этого внутри кристалла ферромагнетика возникают намагниченные области протяженностью 10^-2 - 10^-4 см. Эти самопроизвольно намагниченные области называются доменами (рис. 191, а).

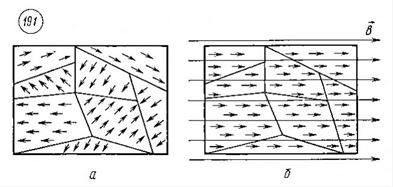
В отдельных доменах магнитные поля имеют различные направления и в большом кристалле взаимно компенсируют друг друга. При внесении ферромагнитного образца во внешнее магнитное поле происходит упорядочение ориентации магнитных полей отдельных доменов.
С увеличением магнитной индукции 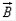внешнего поля возрастает степень упорядоченности ориентации отдельных доменов — магнитная индукция 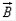возрастает. При некотором значении индукции внешнего поля наступает полное упорядочение ориентации доменов (рис. 191, б), возрастание магнитной индукции прекращается. Это явление называется магнитным насыщением.

Отражающая способность тела

Отражающая способность тела — {\displaystyle b_{\omega ,T}} функция частоты и температуры, показывающая, какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот {\displaystyle d\omega } вблизи {\displaystyle \omega }{\displaystyle b_{\omega ,T}={\frac {d\Phi ''_{\omega ,T}}{d\Phi _{\omega ,T}}}}где {\displaystyle d\Phi ''} — поток энергии, отражающейся от тела.{\displaystyle d\Phi } — поток энергии, падающий на тело в области {\displaystyle d\omega } вблизи {\displaystyle \omega }

Подробнее Альбедо

Абсолютно чёрное тело

Абсолютно черное тело — это физическая абстракция (модель), под которой понимают тело, полностью поглощающее всё падающее на него электромагнитное излучение{\displaystyle a_{\omega ,T}=1} — для абсолютно чёрного тела

Подробнее Абсолютно черное тело

Серое тело

Серое тело — это такое тело, коэффициент поглощения которого не зависит от частоты, а зависит только от температуры{\displaystyle a_{\omega ,T}=a_{T}<1} — для серого тела

Акон Кирхгоффа

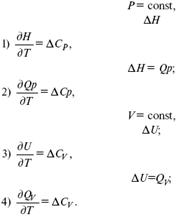
Это уравнения Кирхгоффа в дифференциальной форме.

Когда идет изменение функции по t – температурный коэффициент: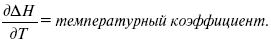

Закон Кирхгоффа:

температурный коэффициент теплового эффекта равен изменению теплоемкости данного процесса.

Интегральная форма уравнений Кирхгоффа:

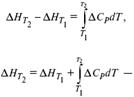
интегральная форма уравнений Кирхгоффа, Т 1= 298 К.

1) ΔСР ≠ f(T)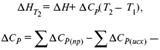

усредненное ΔН при Т 1– по закону Гесса;

2) ΔСР = f(T)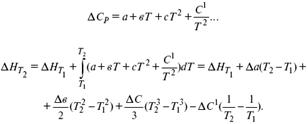

Вопрос. Квантовая гипотеза излучения Планка. Формула Планка. Значение теории Планка.

Гипо́теза Пла́нка — гипотеза, выдвинутая 14 декабря 1900 года Максом Планком и заключающаяся в том, что при тепловом излучении энергия испускается и поглощается не непрерывно, а отдельными квантами (порциями). Каждая такая порция-квант имеет энергию {\displaystyle {\mathcal {E}}}, пропорциональную частоте ν излучения:

{\displaystyle {\mathcal {E}}=h\nu =\hbar \omega }где h или {\displaystyle \hbar ={\frac {h}{2\pi }}} — коэффициент пропорциональности, названный впоследствии постоянной Планка. На основе этой гипотезы он предложил теоретический вывод соотношения между температурой тела и испускаемым этим телом излучением — формулу Планка.

Позднее гипотеза Планка была подтверждена экспериментально.

Выдвижение этой гипотезы считается моментом рождения квантовой механики.

Тепловые источники света

Электрическим источником оптического излучения, и в частности источником света, называют устройство для преобразования электрической энергии в лучистую энергию оптического спектра.

В применяемых электрических источниках оптического излучения электрическая энергия преобразуется в лучистую двумя основными способами: нагревом тела электрическим током и электрическим разрядом в газах и парах металлов. В соответствии с этим электрические источники оптического излучения (лампы) подразделяют на тепловые и разрядные. Возможна и комбинация указанных способов в одном источнике. Различные лампы отличаются между собой электроэнергетическими, светотехническими и эксплуатационными параметрами и характеристиками.

Тепловые источники света выполняют в виде различных ламп накаливания. Несмотря на многообразие ламп накаливания, все они работают по единому физическому принципу преобразования электрической энергии в оптическое излучение путем нагрева электрическим током вольфрамовой нити до температуры 2200...2800 °С, а также имеют сходные основные конструктивные элементы.

Для защиты от окисления тело накала лампы, выполненное в виде вольфрамовой нити, помещают в стеклянную колбу, из которой удаляют воздух и которую для газонаполненных ламп заполняют инертным газом (аргоном, криптоном, азотом или их смесью). Для включения лампы в электрическую цепь её снабжают цоколем, который для различных условий эксплуатации может быть резьбовым, штифтовым, цилиндрическим фиксирующимся и т. д. Наряду с прозрачными стеклянными колбами для снижения яркости лампы применяют матированные, опаловые или "молочные" колбы. Однако в таких колбах теряется до 20% светового потока лампы. В отдельных случаях цокольная часть внутренней поверхности колбы имеет отражатель, выполненный в виде зеркального напыления.

Излучательная способность тела нагрева согласно закону Стефана-Больцмана зависит от температуры его нагрева в четвертой степени. С другой стороны, закон смещения Вина устанавливает связь положения максимума в спектре излучения черного тела с температурой его нагрева

l_max = С /Т,

l_max- длина волны, соответствующая максимуму в спектре излучения черного тела, нм;

С = 2898×10³ нм×К - постоянная Вина; Т - абсолютная температура тела, К.

Из анализа формулы следует, что с увеличением температуры нагрева максимум излучения черного тела смещается в более коротковолновую часть спектра. Установлено, что при максимуме излучения в видимой части спектра световой КПД потока излучения, выражаемый как отношение светового потока Фс к полному лучистому Фл, достигает максимума 14,5% при температуре около 6500 К. Реальные тела, используемые в качестве тепловых излучателей, не могут быть нагреты до такой температуры из-за нарушения их механической прочности (температура плавления вольфрама 3665 К). Поэтому реальный световой КПД ламп накаливания Фс /Фл с вольфрамовой нитью не превышает 4%. При этом в видимой части спектра ламп накаливания преобладают оранжево-красные излучения с длинами волн 600...760 нм. Сине-фиолетовых излучений с длинами волн 380...480 нм примерно в 10 раз меньше.

Так как максимум излучения ламп накаливания расположен в инфракрасной части спектра излучения и в целом у них высокое значение энергетического КПД Фл /Рл ⁼ 0,7...0,9, то они также находят широкое применение для различных целей инфракрасного нагрева. У специальных инфракрасных ламп температура тела накала меньше, чем у обычных осветительных. Поэтому их срок службы в б... 10 раз больше, чем у осветительных, для которых номинальный срок службы (средняя продолжительность горения) составляет 1000 ч.

Для уменьшения отрицательного влияния распыления вольфрамовой нити накала на показатели лампы накаливания внутрь стеклянной колбы вводят в ряде случаев небольшое количество йода или брома. Такие лампы называют галогенными.

Внешнее отличие галогенных осветительных ламп накаливания состоит в том, что их колба выполнена из кварцевого стекла в виде цилиндрической трубки малого объема, у которой на концах имеются выводы для подключения. Вольфрамовая спираль на поддержках вытянута по оси трубки. Поэтому для нормальной работы галогенные лампы устанавливают только в горизонтальном положении.

Галогенные лампы накаливания по сравнению с лампами накаливания общего назначения имеют большую световую отдачу: 20... 35 лм/Вт против 8...20 лм/Вт. Их номинальный срок службы в 2 раза больше. Световой поток к концу срока службы у галогенных ламп снижается всего на 2% вместо 20% у ламп накаливания общего назначения.

Существенные преимущества ламп накаливания - простота устройства, удобство в эксплуатации и относительно малая стоимость.

Отклонения питающего напряжения от номинального значения существенно влияют на характеристики ламп накаливания и, прежде всего, на их срок службы. Например, повышение температуры нити накала всего на 1 % увеличивает распыление вольфрама почти в 2 раза. Учитывая это обстоятельство, лампы накаливания выпускают на определенные диапазоны питающего напряжения: 125...135, 215...225, 220...230 В и т. д.

Мощность ламп накаливания общего назначения от долей ватта до 1000 Вт, галогенных - до 20 кВт.

Обозначение ламп накаливания общего назначения состоит из одной или нескольких букв: В - вакуумная, Г - газонаполненная (86% аргон, 14% азот); БК - биспиральная криптоновая (86% криптон, 14% азот) и т. д. Цифры после буквенного обозначения показывают диапазон уровней питающего напряжения в вольтах, далее номинальную мощность лампы в ваттах и затем порядковый номер разработки. Например, Г-215-225-200 - лампа накаливания газонаполненная моноспиралная на диапазон напряжений 215...225 В номинальной мощностью 200 Вт при среднем расчетном напряжении питания 220 В.

Линейные галогенные лампы накаливания осветительные обозначают буквами КГ (кварцевая галогенная), инфракрасные - КГТ (кварцевая галогенная теплоизлучающая).

Лампы накаливания инфракрасные негалогенные обозначают буквами ИК, лампы с зеркальным отражателем дополнительно имеют букву 3, и, если колба цветная, далее следует буква цвета колбы: К - красная, С - синяя. Например, ИКЗК-215-225-250-1 - лампа накаливания инфракрасная (ИК), с зеркальным отражателем (3), колба красная (К), диапазон напряжений питания 215...225 В, мощностью 250 Вт, номер разработки 1.

ПИРОМЕТРИЯ ОПТИЧЕСКАЯ (от греч. руr - огонь и metreo - измеряю) - совокупность оптических (бесконтактных) методов измерения темп-ры. Почти все оптич. методы основаны на измерении интенсивности теплового излучения (иногда - поглощения) тел. Интенсивность теплового излучения резко убывает с уменьшением темы-ры Т тел, поэтому методы П. о. применяют для измерения относительно высоких темп-р. При Т 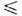1000 °С они играют второстепенную роль, но при Т > 1000 °С становятся основными, а при Т > 3000 °С - практически единств. методами измеренияТ. Это связано с тем, что методы П. о. не требуют контакта датчика измерит. прибора с телом, темп-pa к-рого измеряется. Методами П. о. в промышл. и лаб. условиях определяют темп-р у в печах и др. нагреват. установках, темп-ру расплавл. металлов и изделий из них (проката и т. п.), темп-ру пламён, нагретых газов, плазмы. Осн. условие применимости методов П. о. - излучение тела должно быть тепловым, т. е. подчиняться Кирхгофа закону излучения. Твёрдые тела и жидкости при высоких темп-pax обычно удовлетворяют этому требованию, в случае же газов и плазмы необходима спец. проверка его выполнения. Так, излучение однородного слоя плазмы подчиняется закону Кирхгофа, если распределения молекул, атомов, ионов и электронов плазмы по скоростям соответствуют Максвелла распределению, населённости возбуждённых уровней - распределению Больцмана (см. Больцмана статистика ),а диссоциация молекул и ионизация атомов определяются законом действующих масс, причём во все эти соотношения входит одно и то же значение Т. Такое состояние плазмы наз. термически равновесным. Интенсивность излучения однородной равновесной плазмы однозначно определяется её хим. составом, давлением, атомными константами и равновесной темп-рой. Если плазма неоднородна, то даже в условиях термич. равновесия её непосредственно наблюдаемое излучение не подчиняется закону Кирхгофа. В этом случае необходимо спец. приёмами определить локальные интенсивности излучения. Методы П. о. плазмы многообразны и сложны, они являются составной частью диагностики плазмы. Напротив, для твёрдых тел и жидкостей, спектр излучения к-рых чаще всего сплошной, методы П. о. довольно просты. В этом случае измерение темп-ры осуществляют пирометрами, действие к-рых основано на применении законов излучения абсолютно чёрного тела. Обычно в исследуемом теле вытачивают полость с небольшим выходным отверстием. Полость по отношению к попадающему в неё излучению обладает коэф. поглощения, близким к единице (т. е. по оптич. свойствам она близка к абсолютно чёрному телу).
Наиб. универсальны методы П. о., осн. на измерении интенсивности спектральных линий. Они обеспечивают макс. точность, если известны вероятность соответствующего квантового перехода и концентрация атомов данного сорта. Если же концентрация атомов не известна с достаточной точностью, то применяют метод относит. интенсивности, в к-ром темп-ры вычисляют по отношению интенсивностей двух или неск. спектральных линий.
В др. группе методов П. о. темп-pa определяется по форме или ширине спектральных линий, к-рые зависят от темп-ры либо непосредственно (доплеровское уширение спектральных линий), либо косвенно (в соответствии со Штарка эффектом и зависимостью плотности плазмы от темп-ры). В нек-рых методах Т определяют по абс. или относит. интенсивности сплошного спектра ("континуума"). Особое значение имеют методы измерения Т по спектру рассеянного плазмой излучения лазера, позволяющие исследовать неоднородную плазму. К недостаткам П. следует отнести трудоёмкость измерений, сложность интерпретации результатов, невысокую точность (например, погрешности измерений температуры плазмы в лучшем случае составляют 3-10%).

15 Вопрос. Фотоэффект. Виды фотоэффекта. Опытные законы внешнего фотоэффекта (анализ ВАХ фотоэффекта). Красная граница фотоэффекта.

Гипотеза Планка, блестяще решившая задачу теплового излучения черного тела, получила подтверждение и дальнейшее развитие при объяснении фотоэффекта – явления, открытие и исследование которого сыграло важную роль в становлении квантовой теории. В 1887 году Г. Герц обнаружил, что при освещении отрицательного электрода ультрафиолетовыми лучами разряд между электродами происходит при меньшем напряжении. Это явление, как показали опыты В. Гальвакса (1888 г.) и А.Г. Столетова (1888–1890 гг.), обусловлено выбиванием под действием света отрицательных зарядов из электрода. Электрон еще не был открыт. Лишь в 1898 году Дж.Дж. Томпсон и Ф. Леонард, измерив удельный заряд испускаемых телом частиц, установили, что это электроны.

Различают фотоэффект внешний, внутренний, вентильный и многофотонный фотоэффект.

Внешним фотоэффектом называется испускание электронов веществом под действием электромагнитного излучения. Внешний фотоэффект наблюдается в твердых телах (металлах, полупроводниках, диэлектриках), а также в газах на отдельных атомах и молекулах (фотоионизация).

Внутренний фотоэффект – это вызванные электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу. В результате концентрация носителей тока внутри тела увеличивается, что приводит к возникновению фотопроводимости (повышению электропроводности полупроводника или диэлектрика при его освещении) или к возникновению электродвижущей силы (ЭДС).

Вентильный фотоэффект является разновидностью внутреннего фотоэффекта, – это возникновение ЭДС (фото ЭДС) при освещении контакта двух разных полупроводников или полупроводника и металла (при отсутствии внешнего электрического поля). Вентильный фотоэффект открывает пути для прямого преобразования солнечной энергии в электрическую.

Многофотонный фотоэффект возможен, если интенсивность света очень большая (например, при использовании лазерных пучков). При этом электрон, испускаемый металлом, может одновременно получить энергию не от одного, а от нескольких фотонов.

Первые фундаментальные исследования фотоэффекта выполнены русским ученым А.Г. Столетовым. Принципиальная схема для исследования фотоэффекта приведена на рис. 2.1.

	Рис. 2.1	Рис. 2.2

Два электрода (катод К из исследуемого материала и анод А, в качестве которого Столетов применял металлическую сетку) в вакуумной трубке подключены к батарее так, что с помощью потенциометра R можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом (через кварцевое стекло), измеряется включенным в цепь миллиамперметром.

В 1899 г. Дж. Дж. Томпсон и Ф. Ленард доказали, что при фотоэффекте свет выбивает из вещества электроны.

Вольт-амперная характеристика (ВАХ) фотоэффекта – зависимость фототока I, образуемого потоком электронов, от напряжения, – приведена на рис. 2.2.

Такая зависимость соответствует двум различным энергетическим освещенностям катода (частота света в обоих случаях одинакова). По мере увеличения U фототок постепенно возрастает, т.е. все большее число фотоэлектронов достигает анода. Пологий характер кривых показывает, что электроны вылетают из катода с различными скоростями.

Максимальное значение фототока насыщения определяется таким значением напряжения U, при котором все электроны, испускаемые катодом, достигают анода:

где n – число электронов, испускаемых катодом в 1 с.

Из ВАХ следует, при U = 0 фототок не исчезает. Следовательно, электроны, выбитые из катода, обладают некоторой начальной скоростью υ, а значит и отличной от нуля кинетической энергией, поэтому они могут достигнуть катода без внешнего поля. Для того, чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение . При ни один из электронов, даже обладающий при вылете из катода максимальной скоростью , не может преодолеть задерживающего поля и достигнуть анода. Следовательно,

т.е. замерив задерживающее напряжение , можно определить максимальные значения скорости и кинетической энергии фотоэлектрона.

При изучении ВАХ разнообразных материалов при разных частотах падающего на катод излучения и разных энергетических освещенностях катода и обобщении полученных данных были установлены три закона внешнего фотоэффекта.

«Кра́сная» грани́ца фотоэффе́кта — минимальная частота {\displaystyle \nu _{min}} или максимальная длина волны {\displaystyle \lambda _{max}} света, при которой ещё возможен внешний фотоэффект, то есть начальная кинетическая энергия фотоэлектронов больше нуля. Частота {\displaystyle \nu _{min}} зависит только от работы выхода {\displaystyle A_{out}} электрона:{\displaystyle \nu _{min}={\frac {A_{out}}{h}}}
{\displaystyle \lambda _{max}={\frac {hc}{A_{out}}}}где {\displaystyle A_{out}} — работа выхода для конкретного фотокатода, h — постоянная Планка, а с — скорость света. Работа выхода {\displaystyle A_{out}} зависит от материала фотокатода и состояния его поверхности. Испускание фотоэлектронов начинается сразу же, как только на фотокатод падает свет с частотой {\displaystyle \nu =\nu _{min}} или с длиной волны {\displaystyle \lambda =\lambda _{max}}.

Вопрос. Эффект Комптона.

Эффект Комптона
_{Compton effect}

ЭффектКомптона – рассеяние электромагнитного излучения на свободном электроне, сопровождающееся уменьшением частоты излучения (открыт А. Комптоном в 1923 г.). В этом процессе электромагнитное излучение ведёт себя как поток отдельных частиц – корпускул (которыми в данном случае являются кванты электромагнитного поля - фотоны), что доказывает двойственную – корпускулярно-волновую – природу электромагнитного излучения. С точки зрения классической электродинамики рассеяние излучения с изменением частоты невозможно.
Комптоновское рассеяние – это рассеяние на свободном электроне отдельного фотона с энергией Е = hν = hc/λ (h – постоянная Планка, ν – частота электромагнитной волны, λ – её длина, с – скорость света) и импульсом р = Е/с. Рассеиваясь на покоящемся электроне, фотон передаёт ему часть своей энергии и импульса и меняет направление своего движения. Электрон в результате рассеяния начинает двигаться. Фотон после рассеяния будет иметь энергию Е' = hν' (и частоту) меньшую, чем его энергия (и частота) до рассеяния. Соответственно после рассеяния длина волны фотона λ' увеличится. Из законов сохранения энергии и импульса следует, что длина волны фотона после рассеяния увеличится на величину

,

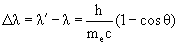где θ – угол рассеяния фотона, а m_e – масса электрона h/m_ec = 0.024 Å называется комптоновской длиной волны электрона.
Изменение длины волны при комптоновском рассеянии не зависит от λ и определяется лишь углом θ рассеяния γ-кванта. Кинетическая энергия электрона определяется соотношением

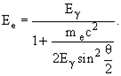
Эффективное сечение рассеяния γ-кванта на электроне не зависит от характеристик вещества поглотителя. Эффективное сечение этого же процесса, рассчитанное на один атом, пропорционально атомному номеру (или числу электронов в атоме) Z.
Сечение комптоновского рассеяния убывает с ростом энергии γ-кванта: σ_k ~ 1/E_γ.

Обратный комптон-эффект

Если электрон, на котором рассеивается фотон, является ультрарелятивистским Ee >> E_γ, то при таком столкновении электрон теряет энергию, а фотон приобретает энергию. Такой процесс рассеяния используется для получения моноэнергетических пучков γ-квантов высокой энергии. С этой целью поток фотонов от лазера рассеивают на большие углы на пучке ускоренных электронов высокой энергии, выведенных из ускорителя. Такой источник γ-квантов высокой энергии и плотности называется Laser-Electron-Gamma-Source (LEGS). В работающем в настоящее время источнике LEGS лазерное излучение с длиной волны 351.1 мкм (~0.6 эВ) в результате рассеяния на электронах, ус