При помощи оборотного и математического маятников.

Цель работы: экспериментально определить ускорение свободного падения с помощью физического и математического маятников. Оборудование и принадлежности:установка с физическим и математическим маятником, секундомер, линейка с миллиметровыми делениями. 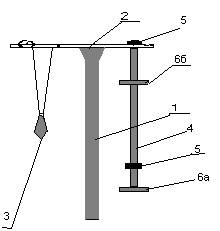    Рис.1. Схематический рисунок установки

ОПИСАНИЕ УСТАНОВКИ.

Общий вид оборотного маятника показан на рис.1. На стойке 1 зафиксирован кронштейн 2, на котором закреплён математический маятник 3 и оборотный маятник 4.

Оборотный маятник выполнен в виде стального стержня, на котором фиксируются две повернутые лезвиями друг к другу опорные призмы 5 и две чечевицы (подвижная 6а и неподвижная 6б).

На стержне с одного конца через 10 мм нанесены углубления. Подвижную чечевицу можно перемещать вдоль стержня и фиксировать в любом положении.

ЭЛЕМЕНТЫ ТЕОРИИ.

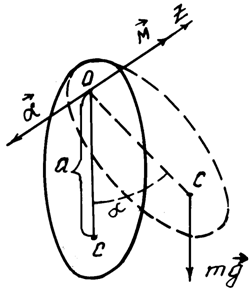
Рис. 2

Общие сведения. Физическим маятником называется твердое тело, способное совершать колебания под действием силы тяжести относительно горизонтальной оси, не проходящей через центр массы (рис. 2). К таким колебаниям применимо основное уравнение динамики вращательного движения твёрдого тела, которое в проекции на ось вращения Z имеет вид:

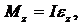(1)

где M_z – проекция момента силы тяжести на ось Z, I – момент инерции маятника относительно оси колебаний, e_z – проекция углового ускорения на ось Z. Учитывая, что M_z = –mgasina, e_z = d²a/dt², получим:

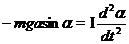, (2)

где m – масса маятника, a – расстояние от оси вращения до центра масс маятника, a – угловое перемещение маятника (угол отклонения маятника от положения равновесия). Угловое перемещение – векторная величина, его направление определяется по правилу буравчика. В данном случае векторы 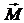и 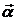направлены в противоположные стороны, поэтому выражение для M_z записано со знаком минус.

При малых углах отклонения sina » a, в этом случае уравнение (2) можно записать в виде:

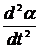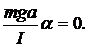+ (3)

Уравнение (3) представляет собой уравнение гармонических колебаний переменной величины a, квадрат угловой частоты которых равен коэффициенту перед a во втором слагаемом. То есть

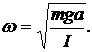(4)

Решение уравнения (3) можно записать в виде

a(t) = a_ocos(wt + j_o), (5)

где a_o – угловая амплитуда колебаний, j_o – начальная фаза колебаний.

Из вышеизложенного следует, что колебания физического маятника (как и математического маятника) не являются гармоническими. Они будут мало отличаться от гармонических колебаний лишь в том случае, когда выполняется условие sina » a, то есть, когда угол отклонения маятника от положения равновесия небольшой.

Из формулы (4) находим период колебаний физического маятника:

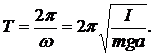(6)

Период колебаний математического маятника длиной L вычисляется по формуле:

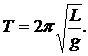(7)

Сравнивая формулы (6) и (7), приходим к выводу, что математический маятник, длина которого

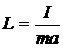, (8)

будет совершать колебания с тем же периодом, что и данный физический маятник. Точка, находящаяся на расстоянии L (рис. 1) от оси вращения физического маятника на прямой, проходящей через его центр масс перпендикулярно оси вращения, называется центром качания физического маятника. Величина L, вычисляемая по формуле (8), называется приведенной длиной физического маятника.

По теореме Гюйгенса – Штейнера

I = I_o + ma², (9)

где I_o – момент инерции физического маятника относительно оси, проходящей через его центр масс параллельно оси колебаний.

Подставив (9) в (8), получим:

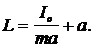(10)

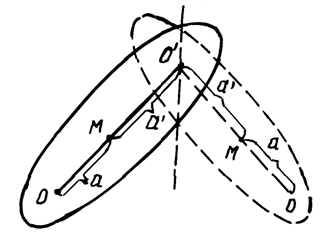
Рис. 3

Из (10) следует, что приведенная длина физического маятника больше расстояния от оси вращения до центра масс маятника на величину (рис. 2, 3)

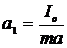. (11)

Подвесим маятник на оси, параллельной прежней и проходящей через центр качания О¢ (рис. 3). В этом случае приведенная длина маятника

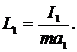(12)

По теореме Гюйгенса – Штейнера 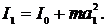Подставив это выражение в (12), а также учитывая, что a₁ = I_o/ma = L - a, получим:

.

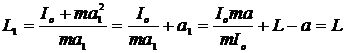Так как приведенная длина физического маятника относительно новой оси не изменилась, то и период его колебаний на новой оси также не изменился. Следовательно, данная ось и параллельная ей ось, проходящая через центр качания маятника, обладают свойством взаимности.

Ускорение свободного падения можно вычислить по формуле

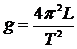. (13)

При определении ускорения свободного падения с помощью оборотного маятника необходимо, изменяя его момент инерции (передвигая чечевицу 6а), добиться того, чтобы расстояние между опорными призмами стало равным приведенной длине оборотного маятника. Измерив L и T, по формуле (13) находим g.

Для определения ускорения свободного падения с помощью математического маятника необходимо измерить его длину L, соответствующий ей период колебаний T, и по формуле (13) вычислить g.

Чтобы повысить точность измерения периода колебаний T, необходимо измерить время t для n колебаний (обычно n = 10). Тогда

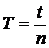. (14)

Порядок выполнения задания 1

1. Установить чечевицу 6а на расстоянии d = 1 см от конца маятника.

2. Пользуясь секундомером, определить t (время n колебаний маятника), передвигая чечевицу 6а каждый раз на 1 см в диапазоне 1 – 15 см, в прямом и перевернутом положениях маятника для каждого положения передвигаемой чечевицы 6а. По формуле (14) найти период колебания. Данные занести в таблицу 1.

Таблица 1.

Результаты измерений периодов колебаний оборотного маятника.

3. На одном чертеже построить графики T(d) зависимости периодов колебаний в прямом и перевернутом положениях маятника от расстояния чечевицы 6а от конца стержня. Точка пересечения графиков будет соответствовать равенству периодов этих колебаний.

4. Установить чечевицу 6а в положение, соответствующее равенству периодов колебаний, и проверить их совпадение. Если T_прям. = T_перев., то расстояние между опорными призмами равно приведенной длине L оборотного маятника.

5. Провести n раз измерения величин L, T, входящих в правую часть равенства (13), определить средние значения <L> и <T>.

6. По формуле (13) определить среднее значение ускорения свободного падения <g>.

Порядок выполнения задания 2.

1. Определить период Т колебаний математического маятника при различной его длине L. Для этого, как и в первом задании, измерить время t для n = 10 колебаний и найти T по формуле (14). Данные занести в таблицу 2.

2. По формуле (13) определить ускорение свободного падения g.

Таблица 2

Результаты измерений и расчётов ускорения свободного падения

с помощью математического маятника.

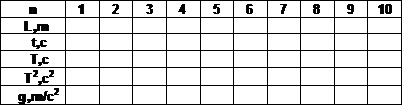
3. Построить график L (T² ).

4. Сравнить значения ускорения свободного падения, полученные в первом и во втором заданиях.