Определение земного ускорения свободного падения
Лабораторная работа №1.
Определение земного ускорения свободного падения
При помощи оборотного и математического маятников.
Цель работы: экспериментально определить ускорение свободного падения с помощью физического и математического маятников. Оборудование и принадлежности:установка с физическим и математическим маятником, секундомер, линейка с миллиметровыми делениями. 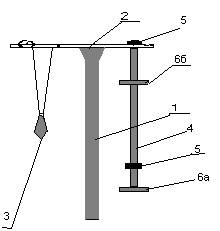 Рис.1. Схематический рисунок установки Рис.1. Схематический рисунок установки |
ОПИСАНИЕ УСТАНОВКИ.
Общий вид оборотного маятника показан на рис.1. На стойке 1 зафиксирован кронштейн 2, на котором закреплён математический маятник 3 и оборотный маятник 4.
Оборотный маятник выполнен в виде стального стержня, на котором фиксируются две повернутые лезвиями друг к другу опорные призмы 5 и две чечевицы (подвижная 6а и неподвижная 6б).
На стержне с одного конца через 10 мм нанесены углубления. Подвижную чечевицу можно перемещать вдоль стержня и фиксировать в любом положении.
ЭЛЕМЕНТЫ ТЕОРИИ.
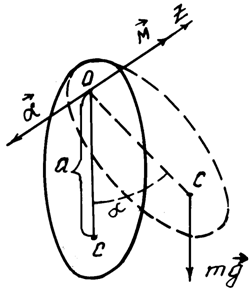
Рис. 2
Общие сведения. Физическим маятником называется твердое тело, способное совершать колебания под действием силы тяжести относительно горизонтальной оси, не проходящей через центр массы (рис. 2). К таким колебаниям применимо основное уравнение динамики вращательного движения твёрдого тела, которое в проекции на ось вращения Z имеет вид:
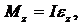 (1)
(1)
где Mz – проекция момента силы тяжести на ось Z, I – момент инерции маятника относительно оси колебаний, ez – проекция углового ускорения на ось Z. Учитывая, что Mz = –mgasina, ez = d2a/dt2, получим:

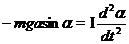 , (2)
, (2)
где m – масса маятника, a – расстояние от оси вращения до центра масс маятника, a – угловое перемещение маятника (угол отклонения маятника от положения равновесия). Угловое перемещение – векторная величина, его направление определяется по правилу буравчика. В данном случае векторы 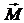 и
и 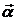 направлены в противоположные стороны, поэтому выражение для Mz записано со знаком минус.
направлены в противоположные стороны, поэтому выражение для Mz записано со знаком минус.
При малых углах отклонения sina » a, в этом случае уравнение (2) можно записать в виде:
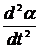 +
+ 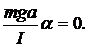 (3)
(3)
Уравнение (3) представляет собой уравнение гармонических колебаний переменной величины a, квадрат угловой частоты которых равен коэффициенту перед a во втором слагаемом. То есть
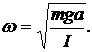 (4)
(4)
Решение уравнения (3) можно записать в виде
a(t) = aocos(wt + jo), (5)
где ao – угловая амплитуда колебаний, jo – начальная фаза колебаний.
Из вышеизложенного следует, что колебания физического маятника (как и математического маятника) не являются гармоническими. Они будут мало отличаться от гармонических колебаний лишь в том случае, когда выполняется условие sina » a, то есть, когда угол отклонения маятника от положения равновесия небольшой.
Из формулы (4) находим период колебаний физического маятника:
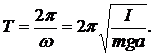 (6)
(6)
Период колебаний математического маятника длиной L вычисляется по формуле:
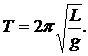 (7)
(7)
Сравнивая формулы (6) и (7), приходим к выводу, что математический маятник, длина которого
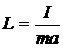 , (8)
, (8)
будет совершать колебания с тем же периодом, что и данный физический маятник. Точка, находящаяся на расстоянии L (рис. 1) от оси вращения физического маятника на прямой, проходящей через его центр масс перпендикулярно оси вращения, называется центром качания физического маятника. Величина L, вычисляемая по формуле (8), называется приведенной длиной физического маятника.
По теореме Гюйгенса – Штейнера
I = Io + ma2, (9)
где Io – момент инерции физического маятника относительно оси, проходящей через его центр масс параллельно оси колебаний.
Подставив (9) в (8), получим:
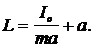 (10)
(10)
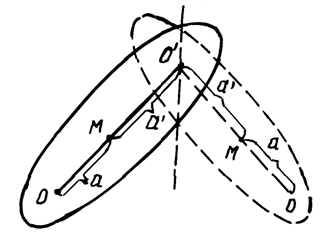
Рис. 3
Из (10) следует, что приведенная длина физического маятника больше расстояния от оси вращения до центра масс маятника на величину (рис. 2, 3)
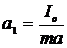 . (11)
. (11)
Подвесим маятник на оси, параллельной прежней и проходящей через центр качания О¢ (рис. 3). В этом случае приведенная длина маятника
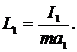 (12)
(12)
По теореме Гюйгенса – Штейнера 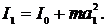 Подставив это выражение в (12), а также учитывая, что a1 = Io/ma = L - a, получим:
Подставив это выражение в (12), а также учитывая, что a1 = Io/ma = L - a, получим:
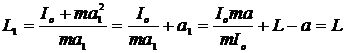 .
.
Так как приведенная длина физического маятника относительно новой оси не изменилась, то и период его колебаний на новой оси также не изменился. Следовательно, данная ось и параллельная ей ось, проходящая через центр качания маятника, обладают свойством взаимности.
Ускорение свободного падения можно вычислить по формуле
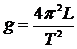 . (13)
. (13)
При определении ускорения свободного падения с помощью оборотного маятника необходимо, изменяя его момент инерции (передвигая чечевицу 6а), добиться того, чтобы расстояние между опорными призмами стало равным приведенной длине оборотного маятника. Измерив L и T, по формуле (13) находим g.
Для определения ускорения свободного падения с помощью математического маятника необходимо измерить его длину L, соответствующий ей период колебаний T, и по формуле (13) вычислить g.
Чтобы повысить точность измерения периода колебаний T, необходимо измерить время t для n колебаний (обычно n = 10). Тогда
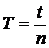 . (14)
. (14)
Порядок выполнения задания 1
1. Установить чечевицу 6а на расстоянии d = 1 см от конца маятника.
2. Пользуясь секундомером, определить t (время n колебаний маятника), передвигая чечевицу 6а каждый раз на 1 см в диапазоне 1 – 15 см, в прямом и перевернутом положениях маятника для каждого положения передвигаемой чечевицы 6а. По формуле (14) найти период колебания. Данные занести в таблицу 1.
Таблица 1.
Результаты измерений периодов колебаний оборотного маятника.

3. На одном чертеже построить графики T(d) зависимости периодов колебаний в прямом и перевернутом положениях маятника от расстояния чечевицы 6а от конца стержня. Точка пересечения графиков будет соответствовать равенству периодов этих колебаний.
4. Установить чечевицу 6а в положение, соответствующее равенству периодов колебаний, и проверить их совпадение. Если Tпрям. = Tперев., то расстояние между опорными призмами равно приведенной длине L оборотного маятника.
5. Провести n раз измерения величин L, T, входящих в правую часть равенства (13), определить средние значения <L> и <T>.
6. По формуле (13) определить среднее значение ускорения свободного падения <g>.
Порядок выполнения задания 2.
1. Определить период Т колебаний математического маятника при различной его длине L. Для этого, как и в первом задании, измерить время t для n = 10 колебаний и найти T по формуле (14). Данные занести в таблицу 2.
2. По формуле (13) определить ускорение свободного падения g.
Таблица 2
Результаты измерений и расчётов ускорения свободного падения
с помощью математического маятника.
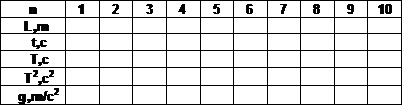
3. Построить график L (T2 ).
4. Сравнить значения ускорения свободного падения, полученные в первом и во втором заданиях.
Лабораторная работа №2
ЭЛЕМЕНТЫ ТЕОРИИ
Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса) и описываются уравнением типа
x = А соs (wt + j0),
где А – максимальное значение колеблющейся величины, называемое амплитудой колебания,w – круговая (циклическая) частота, j0 или a0 – начальная фаза колебания в момент t=0, (wt + j0) – фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то х может принимать значения от +А до –А.
Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемой периодом колебания,за который фаза колебания получает приращение 2p.
Т= 2p/w
Величина, обратная периоду колебаний, n = 1/Т называется частотой колебанийи равна числу полных колебаний, совершаемых в единицу времени. Откуда w=2pn. Единица частоты n - герц (Гц). 1 Гц – частота периодического процесса, при которой за 1 с совершается 1 цикл процесса.
Гармонические колебания могут изображаться графически методом вращающегося вектора амплитуды,илиметодом векторных диаграмм.
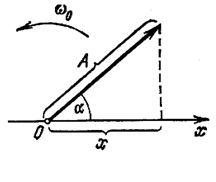 Возьмем ось, вдоль которой будем откладывать колеблющуюся величину x (рис.1). Из взятой на оси точки О отложим вектор длины A, образующий с осью угол a. Если привести этот вектор во вращение с угловой скоростью ω, то проекция конца вектора будет перемещаться по оси x в пределах от -А до +A, причем координата этой проекции будет изменяться со временем по закону
Возьмем ось, вдоль которой будем откладывать колеблющуюся величину x (рис.1). Из взятой на оси точки О отложим вектор длины A, образующий с осью угол a. Если привести этот вектор во вращение с угловой скоростью ω, то проекция конца вектора будет перемещаться по оси x в пределах от -А до +A, причем координата этой проекции будет изменяться со временем по закону
Рис. 1.
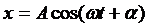
Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.
Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление образует с осью x угол, равный начальной фазе колебаний.
Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты. Результирующее колебаниебудет суммой колебаний х1 и x2, которые определяются функциями
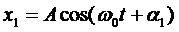 ,
, 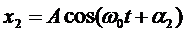 (1)
(1)
¯Представим оба колебания с помощью векторов A1и А2 (рис.2). Построим по правилам сложения векторов результирующий вектор А. На рисунке видно, что проекция этого вектора на ось x равна сумме проекций складываемых векторов:
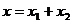
Поэтому вектор Aпредставляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью ω0, как и векторы А1 и А2, так что сумма x1 и х2 является гармоническим колебанием с
Рис. 2. частотой ω0, амплитудой A и начальной
фазой α.
Используя теорему косинусов получаем, что
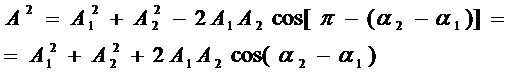 (2)
(2)
Также из рисунка видно, что
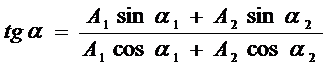 (3)
(3)
Представление гармонических колебаний с помощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.
Биения.
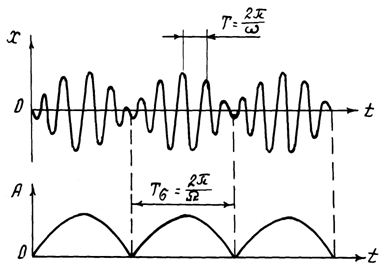
Рассмотрим сложение двух гармонических колебаний, происходящих вдоль одной прямой с частотами ω1 и ω2, незначительно отличающихся друг от друга. (Ω=( |ω1 - ω2 |<< ω1 и Ω<< ω2 ).Пусть в начальный момент времени фазы складываемых колебаний одинаковы. Тогда эти колебания запишутся в виде
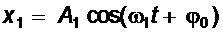 и
и 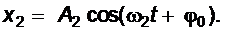 (4)
(4)
Найдем сумму двух таких колебаний, предположив для простоты сначала, что их амплитуды одинаковы (A1 = A2): 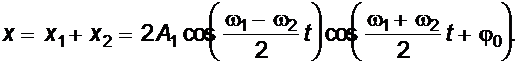 (5)
(5)
|
Рис. 3.
Отсюда видно, что результирующее колебание (биение) происходит с частотой (ω1+ω2)/2, а амплитуда колебаний со временем изменяется в пределах от 2A1 до 0 по закону 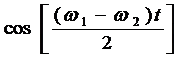 (рис. 3). Значение 2A1 достигается тогда, когда фазы складываемых колебаний совпадают, а нуль - когда фазы противоположны. Периодическое изменение результирующей амплитуды, получающееся при сложении колебаний, совершающихся с близкими частотами и вдоль одной прямой, называют биениями. Циклическая частота биений Ω= |ω1 - ω2 |, период биений Т = 2π/ Ω (рис.3) и частота биений
(рис. 3). Значение 2A1 достигается тогда, когда фазы складываемых колебаний совпадают, а нуль - когда фазы противоположны. Периодическое изменение результирующей амплитуды, получающееся при сложении колебаний, совершающихся с близкими частотами и вдоль одной прямой, называют биениями. Циклическая частота биений Ω= |ω1 - ω2 |, период биений Т = 2π/ Ω (рис.3) и частота биений
νб = 1/Tб = |ν1 - ν2 |, где ν1 и ν2- частоты складываемых колебаний.
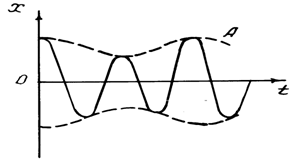 Рис. 4. Рис. 4. |
Если амплитуды складываемых колебаний не равны (A1 # A2), то максимальное значение амплитуды результирующего колебания равно A1+A2, а минимальное - А1-А2. В этом случае биения выражены менее четко (рис.4). Частоты Ω, νб и период Tб определяются разностью частот складываемых колебаний и не зависят от их амплитуд и начальных фаз.
Сложение колебаний во взаимно перпендикулярных направлениях.
Представим две взаимно перпендикулярные векторные величины x и y, изменяющиеся со временем с одинаковой частотой ω по гармоническому закону
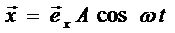
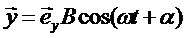 (6)
(6)
где exи eу — орты координатных осей xи y, Аи B — амплитуды колебаний. Величинами xи у может быть, например, смещения материальной точки (частицы) из положения равновесия. В случае колеблющейся частицы величины
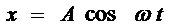 ,
, 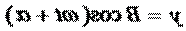 , (7)
, (7)
определяют координаты частицы на плоскости xy. Частица будет двигаться по некоторой траектории, вид которой зависит от разности фаз обоих колебаний. Выражения (6) представляют собой заданное в параметрической форме уравнение этой траектории. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (6) параметр t. Из первого уравнения следует, что
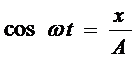 (8)
(8)
Соответственно
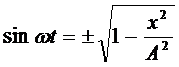 (9)
(9)
Развернем косинус во втором из уравнений (6) по формуле для косинуса суммы:
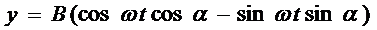
Подставим вместо cosωtи sinωt их значения (3) и (4):
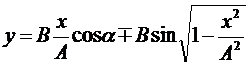

Преобразуем это уравнение
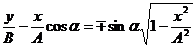
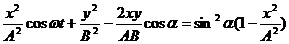
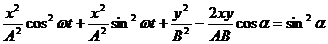
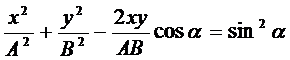 (10)
(10)
Это уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и его полуоси зависят довольно сложным образом от амплитуд A и В и разности фаз α.
Попробуем найти форму траектории для нескольких частных случаев.
1. Разность фаз α равна нулю.
В этом случае уравнение (10) упрощается следующим образом:
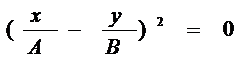 (11)
(11)
Отсюда получается уравнение прямой:
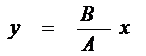
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой, равной 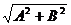 (рис. 5а).
(рис. 5а).
2. Разность фаз α равна ±π.
Уравнение (10) имеет вид
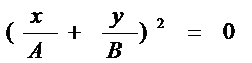 (12)
(12)
Следовательно, результирующее движение представляет собой гармоническое колебание вдоль прямой
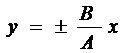 (рис. 5б)
(рис. 5б)
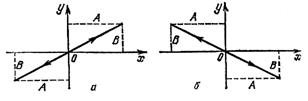
Рис.5.
3. Разность фаз 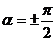 .
.
Уравнение (10) переходит в уравнение эллипса, приведенного к координатным осям:
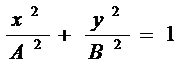 (13)
(13)
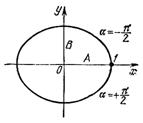
Рис.6.
Полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд А и В эллипс превращается в окружность.
Случаи 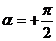 и
и 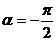 отличаются направлением движения по эллипсу или окружности.
отличаются направлением движения по эллипсу или окружности.
Следовательно, равномерное движение по окружности радиуса R с угловой скоростью ω может быть представлено как сумма двух взаимно перпендикулярных колебаний:
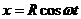 ,
, 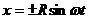
(знак плюс в выражении для у соответствует движению против часовой стрелки, знак минус — движению по часовой стрелке).
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектории результирующего движения имеют вид сложных кривых, называемых фигурами Лиссажу.
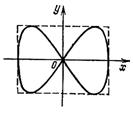
Рис.7. Фигура Лиссажу для
отношения частот 1:2 и
разности фаз π/2
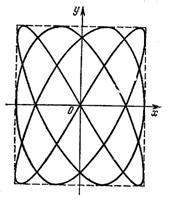
Рис.8. Фигура Лиссажу для отношения частот 3:4
и разности фаз π/2
Наблюдать биения и фигуры Лиссажу можно с помощью электронного осциллографа и звуковых генераторов.
Порядок выполнения задания.
1. Ознакомиться с инструкциями к осциллографу и звуковым генераторам, подобрать режим их работы.
Описание установки:
1)Схема установки (см. рис.9.) :
1. Звуковой генератор( в нем совмещены два звуковых генератора, необходимых в данной работе)
U1-источник питания стабилизированный. Питает 1-й звуковой генератор (U1 = 5V)
U2- источник питания стабилизированный. Питает 2-й звуковой генератор (U1 = 15V)
1а и 1б – переключатели задаваемой частоты сигналов на выходе из генераторов;
2 – кнопка синхронизации колебаний;
3а и 3б – ручки регулирования амплитуды сигналов на выходе из генераторов
ЗГ.1 и ЗГ2 – выходы звукового генератора.
2.Осциллограф
4 – входное гнездо для подачи исследуемых сигналов;
5 – ручка управления усилителем Y ( V/дел – устанавливает коэффициент вертикального отклонения сигнала; плавно – обеспечивает плавную регулировку коэффициент отклонения в каждом положении переключателя V/дел)
6 – переключатель, который устанавливает вид развертки;
7 – входное гнездо для внешнего синхронизирующего сигнала. Это гнездо используется также для внешнего горизонтального входа, если переключатель 6 установлен в положение X.
8 – ручка управления разверткой (устанавливает скорость развертки)
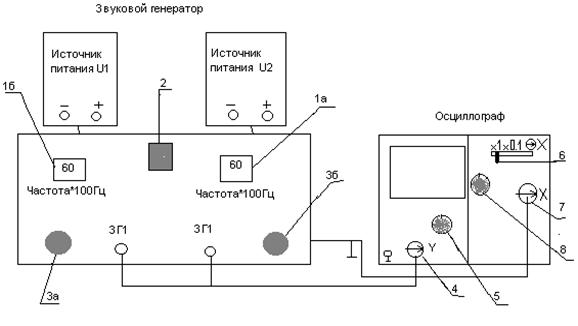
Рис. 9.
Изучить биения.
1.Соединить звуковой генератор с осциллографом как показано на рис.9 (переключатель 6 установить в крайнее левое положение). Условием для получения отчетливой осциллограммы биений является равенство амплитуд складываемых колебаний.
2. Получить задание у преподавателя по изучению биений.
Лабораторная работа №3
Определение коэффициента внутреннего трения жидкости
по методу Пуазейля.
Цель:определить вязкость воды методом Пуазейля.
Оборудование и принадлежности: установка для проведения измерений, мерный стакан, линейка, секундомер.
Схема установки.
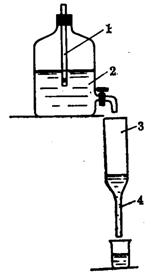
Рис. 1
ОПИСАНИЕ УСТАНОВКИ
Прибор состоит из широкой стеклянной трубки 3, заканчивающейся капилляром 4 (рис. 1). Исследуемая жидкость в трубку 3 поступает из сосуда Мариотта 2. Через пробку в верхней части сосуда 2 пропущена длинная стеклянная трубка 1. В трубку 3 жидкость поступает равномерно, что позволяет установить ее уровень в этой трубке постоянным.
ЭЛЕМЕНТЫ ТЕОРИИ.
Для жидкостей характерна достаточно плотная упаковка молекул (об этом свидетельствует их малая сжимаемость). Поэтому каждая молекула, постоянно сталкиваясь с соседними молекулами, в течение некоторого времени колеблется около определенного положения равновесия. Время от времени молекула, получив от соседней молекулы достаточную энергию, скачком переходит в новое положение равновесия. Дальность этого скачка d примерно равна размеру молекул (10-10м). Среднее время <t>, в течение которого молекула колеблется около данного положения равновесия, называется временем оседлой жизни молекулы. Расчеты показывают, что
 <t>=<t0>exp[DE/(kT)], (1)
<t>=<t0>exp[DE/(kT)], (1)
где <t0> – средний период колебаний молекулы; DE – минимальная энергия, которую нужно сообщить молекуле жидкости, чтобы она могла перейти из одного положения равновесия в другое (DЕ~10-20 Дж); k – постоянная Больцмана; Т – абсолютная температура жидкости. Для воды при комнатной температуре <t0> ~ 10-13с, а <t> ~ 10-11с. С повышением температуры подвижность молекул возрастает, время оседлой жизни уменьшается.
При движении жидкости (или газа) между слоями, перемещающимися с различной скоростью, возникают силы внутреннего трения (вязкости). Эти силы направлены так, что ускоряют медленно движущиеся слои или замедляют быстро движущиеся.
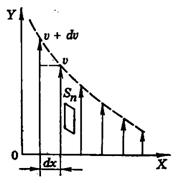
Рис. 2
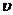
Рассмотрим ламинарный поток жидкости в направлении оси Y (рис. 2). Слои жидкости движутся с разными скоростями. Скорости двух слоев, отстоящих друг от друга на расстоянии dx, отличаются на du. Величина 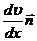 –градиент скорости – показывает, как быстро изменяется скорость слоев вдоль оси Х, здесь
–градиент скорости – показывает, как быстро изменяется скорость слоев вдоль оси Х, здесь 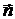 – единичный вектор в направлении максимального возрастания скорости (в нашем случае в отрицательном направлении оси Х).
– единичный вектор в направлении максимального возрастания скорости (в нашем случае в отрицательном направлении оси Х).
Ньютон установил, что модуль силы внутреннего трения между слоями прямо пропорционален площади их соприкосновения и модулю градиента скорости: 
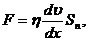 (2)
(2)
где h – коэффициент пропорциональности, называемый вязкостью (или коэффициентом вязкости) жидкости; площадка Sn ориентирована перпендикулярно к градиенту скорости.
Между слоями жидкости будет происходить передача импульса. По второму закону Ньютона
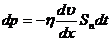 , (3)
, (3)
где dp – величина импульса, переносимого за время dt от слоя к слою через поверхность Sn, перпендикулярную к направлению переноса импульса. Знак минус указывает, что импульс переносится от слоев, движущихся с большей скоростью, к слоям, движущимся с меньшей скоростью (в нашем случае вдоль оси Х).
Импульс, переносимый через единичную площадку, расположенную перпендикулярно к переносимому потоку импульса за единицу времени, называется плотностью потока импульса 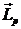 :
:
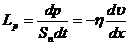 . (4)
. (4)
Соотношения (2)-(4) являются различными формами записи основного закона вязкости - закона Ньютона. Физический смысл коэффициента вязкости h можно определить из любого соотношения. Например, из (4) следует, что вязкость h определяется плотностью потока импульса при градиенте скорости , равном единице.
Вязкость жидкости зависит от ее химического состава, примесей и температуры. С повышением температуры Т вязкость жидкости уменьшается по закону
h=Аexp[DE/(kT)]. (5)
Здесь коэффициент А для каждой конкретной жидкости можно приблизительно считать постоянным.
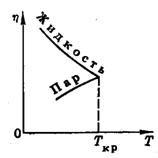
Рис. 3
Вязкость газов (паров) в отличие от жидкостей с повышением температуры медленно увеличивается (~ 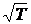 ), при критической температуре Ткр. вязкости жидкости и ее пара сравниваются (рис. 3). Разный характер температурной зависимости вязкости жидкостей и газов указывает на различие механизмов внутреннего трения в них. В газах перенос импульса осуществляется при переходе молекул из слоя в слой благодаря тепловому движению. В жидкостях большую часть времени молекулы колеблются около положения равновесия, скачкообразные переходы редки. Так как молекулы жидкости находятся близко друг к другу, силы молекулярного сцепления между ними значительны. Поэтому одни слои жидкости увлекают (тормозят) соседние слои в основном за счет сил притяжения. Перенос импульса вследствие скачкообразных переходов молекул не играет решающей роли. С повышением температуры расстояния между молекулами увеличиваются, а силы притяжения уменьшаются и, как следствие, уменьшается вязкость.
), при критической температуре Ткр. вязкости жидкости и ее пара сравниваются (рис. 3). Разный характер температурной зависимости вязкости жидкостей и газов указывает на различие механизмов внутреннего трения в них. В газах перенос импульса осуществляется при переходе молекул из слоя в слой благодаря тепловому движению. В жидкостях большую часть времени молекулы колеблются около положения равновесия, скачкообразные переходы редки. Так как молекулы жидкости находятся близко друг к другу, силы молекулярного сцепления между ними значительны. Поэтому одни слои жидкости увлекают (тормозят) соседние слои в основном за счет сил притяжения. Перенос импульса вследствие скачкообразных переходов молекул не играет решающей роли. С повышением температуры расстояния между молекулами увеличиваются, а силы притяжения уменьшаются и, как следствие, уменьшается вязкость.
Величина
n=h/r (6)
называется кинематической вязкостью.
Приборы для измерения вязкости называются вискозиметрами. Существует несколько методов определения вязкости: метод Стокса, основанный на измерении скорости падения шарика в исследуемой жидкости; метод
Пуазейля, в основе которого лежит измерение объема жидкости (газа), протекающей через капиллярную трубку; метод затухающих колебаний тела, подвешенного на упругой нити в исследуемой среде, и другие.
Теория метода. Вязкость жидкости h может быть определена по объему жидкости, протекающей через капиллярную трубку (метод Пуазейля). Этот метод применим только к случаю ламинарного течения жидкости (газа).
Пусть на концах вертикальной капиллярной трубки длиной l и радиусом R создана постоянная разность давлений Dp. Выделим внутри капилляра цилиндрический столбик жидкости радиусом r и высотой h. На боковую поверхность этого столбика действует сила внутреннего трения
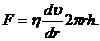 (7)
(7)
Если p1 и p2 - давление на верхнее и нижнее сечения соответственно, то силы давления
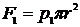 и
и 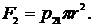 (8)
(8)
Сила тяжести
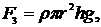 (9)
(9)
где r – плотность жидкости.
При установившемся движении
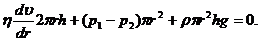 (10)
(10)
Отсюда
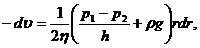 (11)
(11)
где (p1-p2)/h - изменение давления, приходящееся на единицу длины капилляра. Это постоянная вдоль всего капилляра величина. Поэтому
(p1 - p2)/h = Dp/l. (12)
После интегрирования (11) с учетом (12) получим
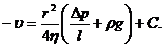 (13)
(13)
При r = R скорость u= 0, следовательно, постоянная интегрирования
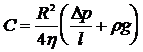 и
и
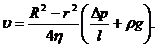 (14)
(14)
Объем жидкости, протекающей через некоторое сечение трубки в пространстве между цилиндрическими поверхностями радиусами r и r + dr за
время t, определяется по формуле dV = 2prdrut или
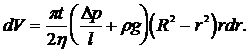 (15)
(15)
Полный объем жидкости, протекающей через сечение капилляра за время t:
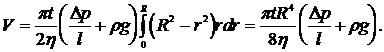 (16)
(16)
Если разность давлений на концах капилляра создается столбом жидкости высотой H, то Dp = rgH. Тогда
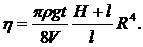 (17)
(17)
Порядок выполнения задания.
1. Подставить под капилляр стакан, открыть кран в сосуде Мариотта и ожидать, пока уровень жидкости в широкой трубке установится постоянным.
2. Определить время t истечения через капилляр определенного объема жидкости V. Объем жидкости определяют с помощью мерного стакана.
3. Измерить высоту столба жидкости H в широкой трубке и длину капилляра l.
4. По формуле (17) рассчитать вязкость жидкости.
5. Провести ряд повторных наблюдений величин H, l, t, V.
6. По формуле (17) определить <h>.
Результаты измерений и вычислений занести в таблицу 1.
Таблица 1.
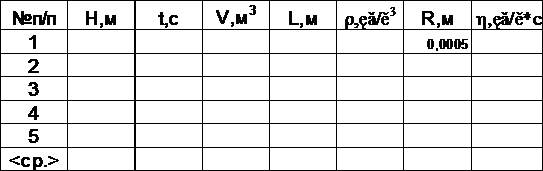
7. Сравнить полученный результат с табличными данными .
Лабораторная работа №3
Определение коэффициента внутреннего трения жидкости
по методу Пуазейля.
Цель:определить вязкость воды методом Пуазейля.
Оборудование и принадлежности: установка для проведения измерений, мерный стакан, линейка, секундомер.
Схема установки.

Рис. 4
ОПИСАНИЕ УСТАНОВКИ
Прибор состоит из широкой стеклянной трубки 3, заканчивающейся капилляром 4 (рис. 1). Исследуемая жидкость в трубку 3 поступает из сосуда Мариотта 2. Через пробку в верхней части сосуда 2 пропущена длинная стеклянная трубка 1. В трубку 3 жидкость поступает равномерно, что позволяет установить ее уровень в этой трубке постоянным.
ЭЛЕМЕНТЫ ТЕОРИИ.
Для жидкостей характерна достаточно плотная упаковка молекул (об этом свидетельствует их малая сжимаемость). Поэтому каждая молекула, постоянно сталкиваясь с соседними молекулами, в течение некоторого времени колеблется около определенного положения равновесия. Время от времени молекула, получив от соседней молекулы достаточную энергию, скачком переходит в новое положение равновесия. Дальность этого скачка d примерно равна размеру молекул (10-10м). Среднее время <t>, в течение которого молекула колеблется около данного положения равновесия, называется временем оседлой жизни молекулы. Расчеты показывают, что
 <t>=<t0>exp[DE/(kT)], (1)
<t>=<t0>exp[DE/(kT)], (1)
где <t0> – средний период колебаний молекулы; DE – минимальная энергия, которую нужно сообщить молекуле жидкости, чтобы она могла перейти из одного положения равновесия в другое (DЕ~10-20 Дж); k – постоянная Больцмана; Т – абсолютная температура жидкости. Для воды при комнатной температуре <t0> ~ 10-13с, а <t> ~ 10-11с. С повышением температуры подвижность молекул возрастает, время оседлой жизни уменьшается.
При движении жидкости (или газа) между слоями, перемещающимися с различной скоростью, возникают силы внутреннего трения (вязкости). Эти силы направлены так, что ускоряют медленно движущиеся слои или замедляют быстро движущиеся.

Рис. 5
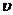
Рассмотрим ламинарный поток жидкости в направлении оси Y (рис. 2). Слои жидкости движутся с разными скоростями. Скорости двух слоев, отстоящих друг от друга на расстоянии dx, отличаются на du. Величина 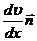 –градиент скорости – показывает, как быстро изменяется скорость слоев вдоль оси Х, здесь
–градиент скорости – показывает, как быстро изменяется скорость слоев вдоль оси Х, здесь 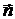 – единичный вектор в направлении максимального возрастания скорости (в нашем случае в отрицательном направлении оси Х).
– единичный вектор в направлении максимального возрастания скорости (в нашем случае в отрицательном направлении оси Х).
Ньютон установил, что модуль силы внутреннего трения между слоями прямо пропорционален площади их соприкосновения и модулю градиента скорости: 
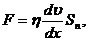 (2)
(2)
где h – коэффициент пропорциональности, называемый вязкостью (или коэффициентом вязкости) жидкости; площадка Sn ориентирована перпендикулярно к градиенту скорости.
Между слоями жидкости будет происходить передача импульса. По второму закону Ньютона
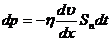 , (3)
, (3)
где dp – величина импульса, переносимого за время dt от слоя к слою через поверхность Sn, перпендикулярную к направлению переноса импульса. Знак минус указывает, что импульс переносится от слоев, движущихся с большей скоростью, к слоям, движущимся с меньшей скоростью (в нашем случае вдоль оси Х).
Импульс, переносимый через единичную площадку, расположенную перпендикулярно к переносимому потоку импульса за единицу времени, называется плотностью потока импульса 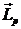 :
:
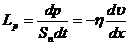 . (4)
. (4)
Соотношения (2)-(4) являются различными формами записи основного закона вязкости - закона Ньютона. Физический смысл коэффициента вязкости h можно определить из любого соотношения. Например, из (4) следует, что вязкость h определяется плотностью потока импульса при градиенте скорости , равном единице.
Вязкость жидкости зависит от ее химического состава, примесей и температуры. С повышением температуры Т вязкость жидкости уменьшается по закону
h=Аexp[DE/(kT)]. (5)
Здесь коэффициент А для каждой конкретной жидкости можно приблизительно считать постоянным.

Рис. 6
Вязкость газов (паров) в отличие от жидкостей с повышением температуры медленно увеличивается (~ 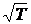 ), при критической температуре Ткр. вязкости жидкости и ее пара сравниваются (рис. 3). Разный характер температурной зависимости вязкости жидкостей и газов указывает на различие механизмов внутреннего трения в них. В газах перенос импульса осуществляется при переходе молекул из слоя в слой благодаря тепловому движению. В жидкостях большую часть времени молекулы колеблются около положения равновесия, скачкообразные переходы редки. Так как молекулы жидкости находятся близко друг к другу, силы молекулярного сцепления между ними значительны. Поэтому одни слои жидкости увлекают (тормозят) соседние слои в основном за счет сил притяжения. Перенос импульса вследствие скачкообразных переходов молекул не играет решающей роли. С повышением температуры расстояния между молекулами увеличиваются, а силы притяжения уменьшаются и, как следствие, уменьшается вязкость.
), при критической температуре Ткр. вязкости жидкости и ее пара сравниваются (рис. 3). Разный характер температурной зависимости вязкости жидкостей и газов указывает на различие механизмов внутреннего трения в них. В газах перенос импульса осуществляется при переходе молекул из слоя в слой благодаря тепловому движению. В жидкостях большую часть времени молекулы колеблются около положения равновесия, скачкообразные переходы редки. Так как молекулы жидкости находятся близко друг к другу, силы молекулярного сцепления между ними значительны. Поэтому одни слои жидкости увлекают (тормозят) соседние слои в основном за счет сил притяжения. Перенос импульса вследствие скачкообразных переходов молекул не играет решающей роли. С повышением температуры расстояния между молекулами увеличиваются, а силы притяжения уменьшаются и, как следствие, уменьшается вязкость.
Величина
n=h/r (6)
называется кинематической вязкостью.
Приборы для измерения вязкости называются вискозиметрами. Существует несколько методов определения вязкости: метод Ст