Степени свободы в статистической физике и термодинамике.

В статистической физике и термодинамике, говоря о степенях свободы, иногда имеют в виду тесно связанное с описанным выше, но несколько модифицированное понятие.

Дело в том, что в этом случае прежде всего интересует полная энергия, приходящаяся на степень свободы. А у каждой колебательной степени свободы имеется как кинетическая, так и потенциальная энергия.

Классическая теорема о распределении энергии по степеням свободы гласит: при термодинамическом равновесии кинетическая энергия в среднем равномерно распределяется по всем степеням свободы, по kT/2 на каждую степень свободы. При этом на каждую степень свободы, имеющую и потенциальную энергию (зависящую от данной координаты), потенциальная энергия также добавляется к полной энергии системы, а для колебательных степеней свободы средняя кинетическая и средняя потенциальная энергия равны (это утверждение является точным для гармонических осцилляторов, однако является хорошим приближением и при некотором ангармонизме).

Таким образом, оказывается, что при вычислении внутренней энергии системы каждая колебательная степень свободы учитывается дважды. Поэтому иногда, для простоты подсчетов используют формулу

где под понимают количество степеней свободы не в обычном смысле, а в смысле распределения полной энергии, то есть каждая колебательная степень свободы учитывается дважды (как «колебательная кинетическая» плюс как «колебательная потенциальная», то есть в этом смысле можно говорить, что каждой колебательной степени свободы соответствуют две степени свободы в термодинамическом смысле. Остальные степени свободы (поступательные и вращательные) учитываются просто, без удвоения (так как этим видам движения соответствует нулевая — говоря точнее, пренебрежимо малая — потенциальная энергия).

Таким образом, в статистической физике нередко под степенями свободы понимают координаты не в конфигурационном пространстве, а в фазовом пространстве, т.е. считают за различные степени свободы обобщенные координаты и обобщенные импульсы. В этом случае вносят одинаковый в классическом приближении (т.е. с некоторыми оговорками - просто при достаточно высоких температурах) вклад в полную энергию - по kT/2 каждая - только те из них, которые входят в выражение для энергии квадратически.

Степени свободы молекулы

Формула внутренней энергии идеального газа:

и прямо связанная с ней формула для средней энергии молекулы идеального газа

Где

i — количество степеней свободы молекулы газа,

— количество газа (m — масса, — молярная масса газа),

R — универсальная газовая постоянная,

k — константа Больцмана,

T — абсолютная температура газа,

- включают количество степеней свободы молекулы.

Все вращательные степени свободы у одноатомных молекул и вращательная степень свободы, соответствующая вращению вокруг продольной оси у линейных (в реальном геометрическом смысле) молекул, выморожены (то есть не должны учитываться в i) всегда, поскольку их температуры вымораживания настолько высоки, что диссоциация молекул происходит гораздо раньше, чем эти температуры достигаются.

46)Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю (невозможно построить замкнутый цикл, проходящий через точку с нулевой температурой).

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Существуют несколько эквивалентных формулировок второго закона термодинамики:

· Постулат Клаузиуса: «Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому» (такой процесс называется процессом Клаузиуса).

· Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло 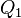у нагревателя, отдав 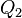холодильнику и совершив при этом работу 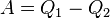. После этого воспользуемся процессом Клаузиуса и вернем тепло 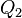от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен.

С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.

Таким образом, постулаты Клаузиуса и Томсона эквивалентны.

Другая формулировка второго начала термодинамики основывается на понятии энтропии:

· «Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (R. J. Clausius, 1865) имеет следующий вид:

Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния 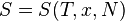, называемая энтропией, такая, что ее полный дифференциал .

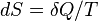В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны.

Ограничения вывода формулы для дифференциала энтропии, данного Клаузиусом, заключаются в предположении об идеальности газа, свойства которого приводят к существованию интегрирующего множителя. Этот недостаток был устранен Каратеодори в работе "Об основаниях термодинамики" (1909). Каратеодори рассматривал множество состояний, достижимых адиабатическим путем (т.е. без теплообмена с окружающей средой). Уравнение, описывающее такое множество этих состояний в дифференциальной форме, является пфаффовой формой. Используя известные из анализа условия интегрируемости пфаффовых форм, Каратеодори пришел к следующей формулировке второго закона:

· В окрестности любого состояния системы существуют состояния, не достижимые адиабатическим путем.

Такая постановка не ограничивает системы, подчиняющихся второму закону термодинамики, только идеальными газами и телами, способными совершать замкнутый цикл при взаимодействии с ними. Физический смысл аксиомы Каратеодори повторяет формулировку Клаузиуса.

Энтропия и критика эволюционизма

Второе начало термодинамики (в формулировке неубывания энтропии) иногда используется критиками эволюционной теории с целью показать, что развитие природы в сторону усложнения невозможно. Однако подобное применение физического закона является некорректным, так как энтропия не убывает только в замкнутых системах (сравн. с диссипативной системой), в то время как живые организмы и планета Земля в целом являются открытыми системами.

В процессе жизнедеятельности живые организмы превращают энергию одного вида (электромагнитную солнечную, химическую) в энергию другого вида (тепловую), тем самым ускоряя суммарное увеличение энтропии Вселенной. Несмотря на "локальное" уменьшение энтропии путем "упорядоченных" процессов, происходит суммарное увеличение энтропии вселенной, а живые организмы являются в некотором роде катализаторами этого процесса. Таким образом, наблюдается выполнение второго закона термодинамики и нет никакого парадокса возникновения и существования живых организмов вопреки глобальной тенденции вселенной к увеличению "беспорядка".

Пусть Земля получает от Солнца за единицу времени энергию 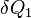в виде излучения с температурой 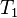, а излучает энергию 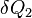в виде излучения с температурой 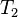. Тогда приращение энтропии составляет 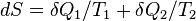. Сколько Земля получает энергии за единицу времени, столько она и излучает в космическое пространство. Поэтому 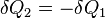, и изменение энтропии составляет 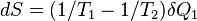. Основная часть энергии, получаемой от Солнца, приходится на видимый оптический диапазон, в то время как излучает Земля в более длинноволновом, инфракрасном диапазоне (не следует путать отражаемый Землёй солнечный свет и излучение самой Земли). Следовательно, 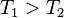, и изменение энтропии отрицательно: 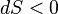. Другими словами, уходящее от Земли излучение обладает большей энтропией, чем приходящее, и оно уносит энтропию от Земли. Поэтому локально энтропия на Земле может убывать. Но при этом энтропия полной системы, включающей в себя помимо Земли также космическое пространство, с которым Земля обменивается энергией, возрастает.

47)цикл Карно́

В термодинамике цикл Карно́или процесс Карно— это обратимый круговой процесс, состоящий из двух адиабатических и двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.

Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году.

Поскольку обратимые процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному обратимому процессу Карно только с большей или меньшей степенью точности. В цикле Карно тепловая машина преобразует теплоту в работу с максимально возможным коэффициентом полезного действия из всех тепловых машин, у которых максимальная и минимальная температуры в рабочем цикле совпадают соответственно с температурами нагревателя и холодильника в цикле Карно

Пусть тепловая машина состоит из нагревателя с температурой 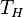, холодильника с температурой и рабочего тела.

Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах T(температура) 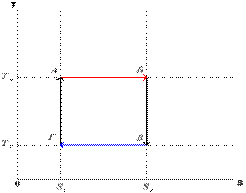и S (энтропия).

1. Изотермическое
расширение (на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру 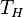, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты 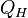. При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.

2. Адиабатическое расширение (на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника 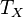, тело совершает механическую работу, а энтропия остаётся постоянной.

3. Изотермическое сжатие (на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру 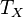, приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты 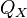. Над телом совершается работа, его энтропия уменьшается.

4. Адиабатическое сжатие (на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

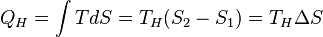Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику

.

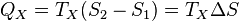Отсюда коэффициент полезного действия тепловой машины Карно равен

.
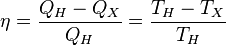