ИСО-Инерциальная система отсчета.События, являющиеся одновременными в одной ИСО, неодновременны в другой ИСО, движущейся относительно первой.

20.Релятивистский импульс.

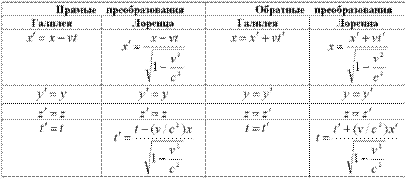Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:

где - инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, - сила действующая на частицу. Сопоставим с классическим уравнением

Мы приходим к выводу, что релятивистский импульс частицы равен

(6.7)

Релятивистская масса.

Определив массу частицы m как коэффициент пропорциональности между скоростью и импульсом, получим, что масса частицы зависит от ее скорости.

(6.8)

Энергия в релятивистской динамике.

Для энергии частицы в теории относительности получается выражение:

(6.9)

Из (2.3) следует, что покоящаяся частица обладает энергией

(6.10)

Эта величина носит название энергии покоя частицы. Kинетическая энергия, очевидно, равна

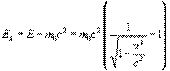(6.11)

Приняв во внимание, что , выражение для полной энергии частицы можно написать в виде

(6.12)

Из последнего выражения вытекает, что энергия и масса тела всегда пропорциональны друг другу. Всякое изменение энергии тела сопровождается изменением массы тела

и, наоборот, всякое изменение массы сопровождается изменениемэнергии . Это утверждение носит название закона взаимосвязи или закона пропорциональности массы и энергии.

Зависимость массы от скорости

Согласно второму закону Ньютона (2.4) постоянная сила, действующая на тело продолжительное время, может сообщить телу сколь угодно большую скорость. Но в действительности скорость света в вакууме является предельной, и ни при каких условиях тело не может двигаться со скоростью, превышающей скорость света в вакууме. Требуется совсем небольшое изменение уравнения движения тел, чтобы это уравнение было верным при больших скоростях движения. Предварительно перейдем к той форме записи второго закона динамики, которой пользовался сам Ньютон:

(2.5)

где — импульс тела. В этом уравнении масса тела считалась независимой от скорости.

Поразительно, что и при больших скоростях движения уравнение (2.5) не меняет своей формы.

Изменения касаются лишь массы. При увеличении скорости тела его масса не остается постоянной, а растет.

Зависимость массы от скорости можно найти, исходя из предположения, что закон сохранения импульса справедлив и при новых представлениях о пространстве и времени. Расчеты слишком сложны. Приведем лишь конечный результат.

Если через m0 обозначить массу покоящегося тела, то масса m того же тела, но двигающегося со скоростью , определяется формулой

(2.6)

На рисунке 43 представлена зависимость массы тела от его скорости. Из рисунка видно, что возрастание массы тем больше, чем ближе скорость движения тела к скорости света с.

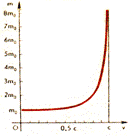Рис. 43

При скоростях движения, много меньших скорости света, выражение чрезвычайно мало отличается от единицы. Так, при скорости современней космической ракеты u»10 км/с получаем =0,99999999944.

21.Кинетическая и полная энергия тела.Масса покоя,энергия покоя

Закон взаимосвязи массы и энегргии: Энергия покоя системы равна произведению массы этой системы на квадрат скорости света в вакууме.

E=mc2 (1)- полная энергия тела или системы тел, из каких бы видов энергии она не состояла бы, Есвязанна с массойmсоотношением(1).

m=m0/(1-v2/c2)1/2-релятивистская масса, мера энергосодержания, зависит от скорости тела.

E=E0+ Ek ,где E0=m0c2–энегрия покоя.

Ek- кинетическая энергия.

m=m0+∆m (релятивистская добавка массы).

E=m0c2/√(1-v2/c2) =m2à m2c2(1- v2/c2)=m02c4,

m2c4- m2v2c2= m02c4 à E2 – p2c2= m02c4- const.

E2= m02c4+ p2c2 à E= √(m02c4+ p2c2)