Величины, характеризующие колебания

Наиболее важными величинами, характеризующими механические колебания, являются:

§ число колебаний за некоторый промежуток времени t. Обозначается буквой N;

§ координата материальной точки или ее смещение (отклонение) — величина, характеризующая положение колеблющейся точки в момент времени t относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в заданный момент времени. Обозначается буквой x, измеряется в метрах (м);

§ амплитуда — максимальное смещение тела или системы тел из положения равновесия. Обозначается буквой A или x_max, измеряется в метрах (м);

§ период — время совершения одного полного колебания. Обозначается буквой T, измеряется в секундах (с);

§ частота — число полных колебаний в единицу времени. Обозначается буквой ν, измеряется в герцах (Гц);

§ циклическая частота, число полных колебаний системы в течение 2π секунд. Обозначается буквой ω, измеряется в радиан в секунду (рад/с);

§ фаза — аргумент периодической функции, определяющий значение физической величины в любой момент времени t. Обозначается буквой φ, измеряется в радианах (рад);

§ начальная фаза — аргумент периодической функции, определяющий значение физической величины в начальный момент времени (t = 0). Обозначается буквой φ₀, измеряется врадианах (рад).

Эти величины связаны между собой следующими соотношениями:

T=tN, ν=1T=Nt,

ω=2π⋅ν=2πT, φ=ω⋅t+φ0.

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения. Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.

Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:

Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:

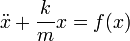, где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.

В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:

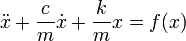
Гармонические колебания

Гармонические колебания — это колебания, при которых координата (смещение) тела изменяется со временем по закону косинуса или синуса и описывается формулами:

x=A⋅sin(ω⋅t+φ0) (1) или x=A⋅cos(ω⋅t+φ0). (2)

Зависимость координаты от времени x(t) называется кинематическим законом гармонического колебания (законом движения).

Графически зависимость смещения колеблющейся точки от времени изображается косинусоидой (или синусоидой).

В этих формулах ω – частота колебания, А – амплитуда колебания, φ0 – начальная фаза колебания. Приведенные формулы отличаются определением начальной фазы и при φ0(1) = φ0 (2) +π/2 полностью совпадают.

Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.

Выражение, стоящее под знаком cos или sin, наз. фазой колебания: . (ω⋅t+φ0)= φ

Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.

Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).