Билет 3. Движение тела, брошенного под углом к горизонту.
Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения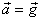 
; проекции ускорения на координатные оси равны ах = 
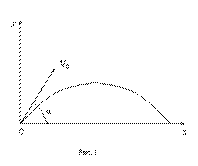0, ау = -g.
Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).
Формула для времени полета: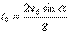 
Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t0.
 . |
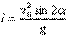Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.
Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
 . |
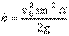Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:
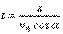
и подставить его во второе уравнение. Тогда получим:
.
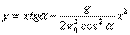Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.
Билет 4) Относительность движения. Инерциальные системы отсчета. Преобразования координат Галлилея. Сложение координат. Принцип относительности Галлилея. Принцип относительности Эйнштейна.
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.
Инерциальные системы отсчета– это системы, относительно которых материальная точка при отсутствиина неевнешних воздействий или их взаимнойкомпенсации покоится или движется равномернои прямолинейно.
Преобразования Галилея — в классической механике (механике Ньютона) преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО) к другой. Термин был предложен Филиппом Франком в 1909 году. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время»[3]) и выполнение принципа относительности (принцип относительности Галилея).Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.