Билет 1) Кинематика материальной точки. Основные характеристики: перемещение, скорость, ускорение. Равномерное и равноускоренное движение - уравнения и графики

Билет 1) Кинематика материальной точки. Основные характеристики: перемещение, скорость, ускорение. Равномерное и равноускоренное движение - уравнения и графики

Механика - область физики, изучающая движение материальных тел и взаимодействие между ними.

Кинема́тика — раздел механики, изучающий математическое описание движения тел без рассмотрения причин движения.

Материальная точка –любое тело, размерами окторого при данных условиях можно пренебречь.

Абсолютно твердое тело – тело, деформациями которого при данных условиях можно пренебречь.

Механическое движение– изменение положения тел в пространстве относительно других тел с течением времени.

Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение тел.

Перемещение - векторная физическая величина, характеризующая изменение положения материальной точки относительно выбранной системы отсчёта. Вектор перемещения соединяет начальное положение точки с конечным.

Траектория– линия, вдоль которой движется тело.

Путь– длина траектории.

Скорость – векторная физическая величина, характеризующая быстроту движения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.

Скорость бывает средней по перемещению и средней путевой. Средняя по перемещению – мгновенная, это вектор (производная пути по времени); а средняя путевая – отношение пройденного пути ко времени, за которое этот путь пройден.

Ускорение – векторная физическая величина, характеризующая изменение скорости за единицу времени.

Равноме́рное движе́ние — механическое движение, при котором тело за любые равные отрезки времени совершает одинаковые перемещения. Равномерное движение материальной точки — это движение, при котором скорость точки остаётся неизменной. Перемещение, пройденное точкой за время 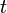, задаётся в этом случае формулой .

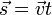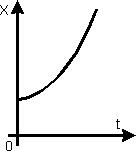
Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты 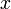точки от времени является линейной:

,

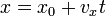где 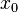— начальная координата точки, 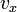— проекция вектора скорости на координатную ось

.

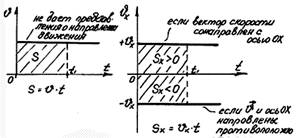
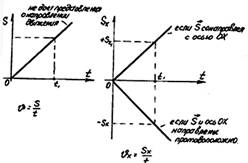
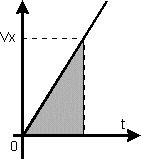
Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.

При равноускоренном движении по прямой скорость тела определяется формулой:

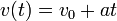
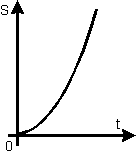
Зная, что 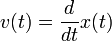, найдём формулу для определения координаты x:

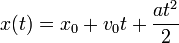
Билет 2) Криволинейное движение. Нормальное (центростремительное) и тангенциальное (касательное) ускорение. Угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением. Радиус кривизны таректории.

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движенииизменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Нормальное ускорение(центростремительное) - величина, характеризующая быстроту изменения направления вектора скорости.

Тангенциальное ускорение – величина характеризующая быстроту изменения модуля скорости материальное точки.

Радиус кривизны – радиус окружности R, по которой движется тело.

Определения

Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Моме́нт и́мпульса - векторная физическая величина, равная векторному произведению радиус-вектора на импульс. Характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

МАЯТНИК ОБЕРБЕКА

Цель работы – изучение основного закона динамики вращательного движения, определение момента инерции системы грузов.

Приборы и принадлежности: лабораторный модуль ЛКМ-3 со стойкой и блоком, стержень с отверстиями, два круглых груза, груз наборный, нить длиной 55 см с крючком (синяя), измерительная система ИСМ-1 (секундомер), пластиковый фиксатор.

Краткая теория

Основной закон динамики вращательного движения твердого тела относительно неподвижной оси

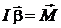(1)

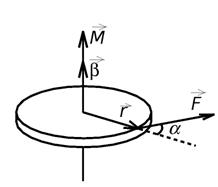
связывает кинематическую характеристику движения – угловое ускорение 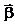с динамическими характеристиками – моментом силы 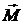и моментом инерции I (рис. 1).

Угловое ускорение характеризует изменение угловой скорости Рис. 1. Момент M силы F

во времени и направлено, как и момент силы, вдоль оси вращения. 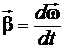(2) .

Угловое ускорение связано с касательной составляющей линейного ускорения а_τточки вращающегося тела соотношением

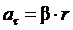, (3)

где r –- кратчайшее расстояние от этой точки до оси вращения.

Моментом силы в общем случае называют векторную величину

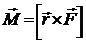, (4)

где 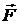– сила, лежащая в плоскости, перпендикулярной оси вращения; 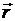– вектор, соединяющий точку на оси c точкой приложения силы.

В уравнении (1) 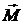– сумма составляющих моментов сил вдоль направления оси вращения.

Момент инерции I характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела. Момент инерции равен сумме произведений элементарных масс Δm_i , на которые мысленно разбито тело, на квадрат их расстояний до оси вращения

I=ΣΔm_i r_{i .} (5)

Выражая Δm_i через плотность тела: Δm_i =ρ ΔV_i ,где ΔV_i – элементарный объем тела, и переходя к пределу при ΔV_i → 0, получим

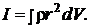(6)

Формула (6) позволяет теоретически найти момент инерции любого тела. Например, момент инерции тонкого однородного стержня длиной l и массой т относительно оси, проходящей перпендикулярно стержню через его центр,

I = т l ² / 12 .

Теорема Штейнера устанавливает связь между моментом инерции I_с твердого тела относительно оси, проходящей через центр инерции, и моментом инерции относительно другой оси, параллельной первой

I = I_с + та² , (7)

где а – расстояние между осями, т – масса тела.

В настоящей работе экспериментально находится момент инерции маятника Обербека (рис.2). Он состоит из блока радиусом R, который может вращаться вокруг неподвижной горизонтальной оси. К блоку прикреплены симметрично относительнооси стержни, на каждом из которых могут свободно перемещаться грузы массами m₁, что дает возможность изменять момент инерции маятника. Грузы m₁ устанавливаются на одинаковом расстоянии от оси, так что центр инерции всей вращающейся части маятника находится на оси вращения.

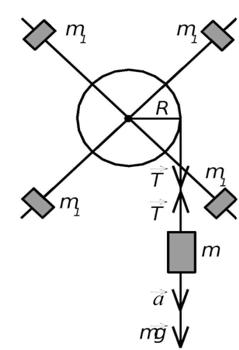
К концу нити прикреплен груз массой m. Из закона динамики вращательного движения следует

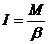. (8)

Момент силы М, создающийся силой натяжения нити, исходя из (4)

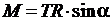, (9)

где α – угол между вектором 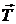и отрезком R на рис. 2, равный 90°; sin α= 1.

Запишем второй закон Ньютона для поступательного движения груза m в проекции на направление ускорения а,

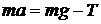. (10)

рис. 2. Маятник Обербека

В этой формуле сила натяжения нити T, действующая на груз, по модулю равна силе натяжения нити, действующей на блок в формуле (9) (поэтому они обозначены одинаково). Это справедливо, если массой нити можно пренебречь по сравнению с массой груза т.

Из (9) и (10) получим

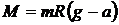. (11)

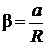Тангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима.

Тогда из (3) следует , (12)

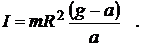(13)

Подставляя (11)и(12)в (8), получим

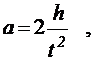Из этой формулы следует, что ускорение (а) не зависит от времени, так как все остальные величины в этом уравнении постоянны, значит, движение маятника будет равноускоренным и при нулевой начальной скорости.

(14)

где h – путь, пройденный грузом т за время t.

В данной работе измеряется время одного полного оборота блока, и за это время груз массой m пройдет путь

h=2πR . (15)

Подставив (14) и (15) в (13), получим формулу для вычисления момента инерции маятника

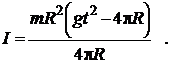
(16)

Момент инерции маятника Обербека будет изменяться при изменении расстояния r от оси вращения маятника до центров грузов массами m₁, перемещаемых вдоль стержней.

Согласно теореме Штейнера (7)

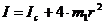, (17)

где I_c – момент инерции всей вращающейся части маятника при условии, что центры грузов m₁находились бы на оси вращения.

Из (17) следует, что зависимость 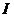от 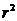– линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.

Гармонические колебания

Гармонические колебания — это колебания, при которых координата (смещение) тела изменяется со временем по закону косинуса или синуса и описывается формулами:

x=A⋅sin(ω⋅t+φ0) (1) или x=A⋅cos(ω⋅t+φ0). (2)

Зависимость координаты от времени x(t) называется кинематическим законом гармонического колебания (законом движения).

Графически зависимость смещения колеблющейся точки от времени изображается косинусоидой (или синусоидой).

В этих формулах ω – частота колебания, А – амплитуда колебания, φ0 – начальная фаза колебания. Приведенные формулы отличаются определением начальной фазы и при φ0(1) = φ0 (2) +π/2 полностью совпадают.

Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.

Выражение, стоящее под знаком cos или sin, наз. фазой колебания: . (ω⋅t+φ0)= φ

Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.

Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).

ФИЗИЧЕСКИЙ МАЯТНИК

Цель работы – изучение физического маятника, определение ускорения свободного падения.

Приборы и принадлежности: лабораторный модуль ЛКМ-3 со стойкой и блоком, стержень с отверстиями, измерительная система ИСМ-1 (секундомер), пластиковый фиксатор.

Краткая теория

Физический маятник – твердое тело, которое может совершать колебания под действием силы тяжести относительно неподвижной оси O(рис. 1).

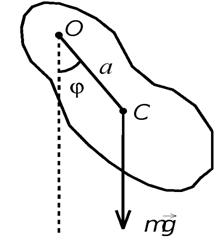
Рис. 1. Физический маятник

Запишем основное уравнение динамики вращательного движения.

.

I β = М ,(1)

где I – момент инерции маятника;

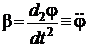– угловое ускорение, φ – угол отклонения маятника от положения равновесия, М - сумма проекций моментов сил на направление оси вращения. Если момент сил трения много меньше момента силы тяжести, то

M= -mga×sinj ,, (2)

где т– масса маятника, g –- ускорение свободного падения, а –- расстояние от оси вращения до центра тяжести.

Уравнение движения (1) с учетом (2) примет вид

Ij = -mga×sinα

где ω_о² = (mga)/I ,тогда получим уравнение:

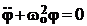. (3)

Уравнение (3) является линейным дифференциальным уравнением относительно функции φ(t).

Если амплитуда колебаний физического маятника не мала, дифференциальное уравнение (3) не будет линейным. Для больших углов отклонений маятника период Т начинает зависеть от амплитуды колебаний φ_{m .} Эту зависимость можно представить суммой бесконечного ряда, первые слагаемые которого равны

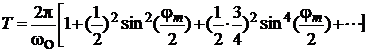. (4)

При малых колебаниях угол φ мал, поэтому sinφ ≈ φ и уравнение (3) становится дифференциальным уравнением гармонических колебаний

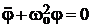. (5)

Решение этого уравнения:

j = j_mcos(ω₀t + α), (6)

где α - начальная фаза колебаний, ω_о = 2π/Т - циклическая частота колебаний.

Запишем формулу периода малых колебаний, как

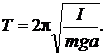(7)

Получим зависимость периода малых колебаний от расстояния а. Момент инерции, согласно теореме Штейнера, равен

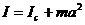, (8)

где I_с - момент инерции маятника относительно оси, проходящей через центр масс. Подставляя (8) в (7), получим

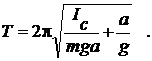(9)

Согласно этой формуле период колебаний Т одинаков при двухразличных значениях а (рис. 2): Т₁ = Т₂ при

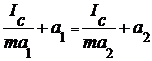, откуда

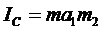. (10)

Подставим (10) в формулу (9). Получим

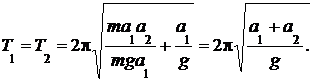(11)

Величина 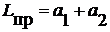(12)

называется приведенной длиной физического маятника.

Сравнивая формулы (11) и (7) получим

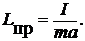(13)

Формула для периода малых колебаний маятника будет иметь следующий вид

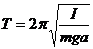. (14)

В данной работе с помощью физического маятника находится ускорение свободного падения g,которое исходя из уравнения (14),

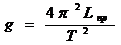. (15)

Приведённая длина — это условная характеристика физического маятника. Она численно равна длине математического маятника, период которого равен периоду данного физического маятника.

Приведенная длина 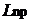находится из формулы (12), в которой а₁и а₂определяются из графика зависимости Т от а, построенного на основе результатов эксперимента.

Для уменьшения погрешности измерения в эксперименте измеряют период колебаний маятника относительно осей, находящихся по обе стороны от центра тяжести. На рис. 2 представлена теоретическая зависимость периода колебаний от параметра a, которая зеркально симметрична относительно оси Т.

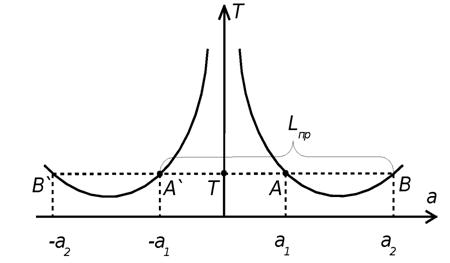Рис. 2. Зависимость периода колебаний маятника от параметрa a

На рисунке приведенная длина маятника L_np = a_{1 +} a₂ равна расстоянию между точками А ̀В или В̀ А.

Молекулы, образующие тело, находятся в состоянии непрерывного беспорядочного движения. При этом они сталкиваются друг с другом и изменяют свою скорость как по направлению, так и по величине. Правда, столкновения в обычном смысле этого слова не происходит, так как соприкосновению молекул припятствует резко возрастающие при их сближении силы отталкивания. Однако действие этих сил приводит к такому же результату, как и обычное столкновение, т.е. к отскакиванию сблизившихся молекул друг от друга.

В молекулярно-кинетической теории пользуются моделью идеального газа, согласно которой считают, что:

1)собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;

2)между молекулами газа отсутствуют силы взаимодейтсвия;

Билет 1) Кинематика материальной точки. Основные характеристики: перемещение, скорость, ускорение. Равномерное и равноускоренное движение - уравнения и графики

Механика - область физики, изучающая движение материальных тел и взаимодействие между ними.

Кинема́тика — раздел механики, изучающий математическое описание движения тел без рассмотрения причин движения.

Материальная точка –любое тело, размерами окторого при данных условиях можно пренебречь.

Абсолютно твердое тело – тело, деформациями которого при данных условиях можно пренебречь.

Механическое движение– изменение положения тел в пространстве относительно других тел с течением времени.

Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение тел.

Перемещение - векторная физическая величина, характеризующая изменение положения материальной точки относительно выбранной системы отсчёта. Вектор перемещения соединяет начальное положение точки с конечным.

Траектория– линия, вдоль которой движется тело.

Путь– длина траектории.

Скорость – векторная физическая величина, характеризующая быстроту движения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.

Скорость бывает средней по перемещению и средней путевой. Средняя по перемещению – мгновенная, это вектор (производная пути по времени); а средняя путевая – отношение пройденного пути ко времени, за которое этот путь пройден.

Ускорение – векторная физическая величина, характеризующая изменение скорости за единицу времени.

Равноме́рное движе́ние — механическое движение, при котором тело за любые равные отрезки времени совершает одинаковые перемещения. Равномерное движение материальной точки — это движение, при котором скорость точки остаётся неизменной. Перемещение, пройденное точкой за время 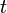, задаётся в этом случае формулой .

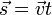Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты 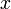точки от времени является линейной:

,

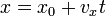где 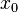— начальная координата точки, 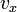— проекция вектора скорости на координатную ось

.

Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.

При равноускоренном движении по прямой скорость тела определяется формулой:

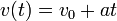
Зная, что 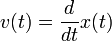, найдём формулу для определения координаты x:

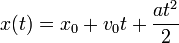
Билет 2) Криволинейное движение. Нормальное (центростремительное) и тангенциальное (касательное) ускорение. Угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением. Радиус кривизны таректории.

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движенииизменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Нормальное ускорение(центростремительное) - величина, характеризующая быстроту изменения направления вектора скорости.

Тангенциальное ускорение – величина характеризующая быстроту изменения модуля скорости материальное точки.

Радиус кривизны – радиус окружности R, по которой движется тело.