Второй закон термодинамики. Вияние энтропийного и энтальпийного факторов на направление химического сродства.

Второй закон термодинамики: в изолированных системах могут самопроизвольно протекать только процессы, идущие с увеличением энтропии (ΔS > 0).

Существует функция состояния - энтропия S, которая обладает следующим свойством: 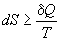, где знак равенства относится к обратимым процессам, а знак больше - к необратимым.

Функцией состояния системы одновременно определяющей влияние энтальпийного и энтропийного факторов на направленность процессов при постоянных T и P является свободная энергия Гиббса G=H-TS.

Процессы могут протекать самопроизвольно, если они сопровождаются уменьшением энтальпии и увеличением энтропии системы. Если же энтальпия системы увеличивается, а энтропия уменьшается, то такой процесс не может протекать. При иных знаках принципиальная возможность протекания процесса определяется соотношением энтропийного и энтольпийного факторов.

По знаку Δ G можно судить о направлении химического превращения в неравновесной смеси реагентов и продуктов. Если ΔrG < 0, то реакция возможна в прямом направлении от реагентов к продуктам. Это значит, что К′ р < Kр и, следовательно, чтобы К′ р росло и приближалось к равновесному значению Кр, должен расти числитель, а это продукты. Если ΔrG > 0 – реакция возможна в обратном направлении. Отметим разный физический смысл очень близких по написанию выражений: ΔrG < 0 (1) ΔrG0 < 0 (2) а также ΔrG > 0 (3) ΔrG0 > 0 (4) Выражение (1) означает, что реакция в системе протекает в сторону образования продуктов при данной температуре и соответствующих неравновесных концентрациях компонент. Выражение (2) означает, что при данной температуре константа равновесия больше единицы. Процесс можно направить в любую сторону. Выражение (3) означает, что реакция в системе протекает в сторону образования исходных веществ при данной температуре и соответствующих неравновесных концентрациях компонент. Выражение (4) означает, что при данной температуре константа равновесия меньше единицы. Процесс также можно направить в любую сторону.

Вопрос 13

Что характеризует первый и второй закон термодинамики и их математические выражения.

Математическое выражение:

1. Первого закона термодинамики: ΔQ=ΔU+pΔV

2. Второго закона термодинамики: dA/dT=Q/T=ΔS

Визохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно,

Q = ΔU = U (T2) – U (T1).

Здесь U (T₁) и U (T₂) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).

В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением

A = p (V2 – V1) = p ΔV.

Первый закон термодинамики для изобарного процесса дает:

Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV.

При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T₂ < T₁; внутренняя энергия убывает, ΔU < 0.

В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.

Вопрос 14

Состояние термодинамического равновесия. Константа равновесия. Использование уравнения изотермы Вант-Гоффа для определения возможности осуществления химических реакций.

Термодинамическое равновесие — состояние системы, при котором ее параметры (температура, давление, объем, энтропия) остаются неизменными по времени в условиях изолированности от окружающей среды.

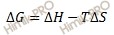
Отсюда при термодинамическом равновесии должно выполниться соотношение:

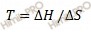
Конста́нта равнове́сия — величина, определяющая для данной химической реакции соотношение между термодинамическими активностями исходных веществ и продуктов в состоянии химического равновесия.

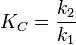
Например, для реакции окисления монооксида углерода:

2CO + O₂ = 2CO₂константа равновесия может быть рассчитана по уравнению:

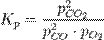
Правило Вант-Гоффа При повышении температуры на каждые 10 градусов константа скорости гомогенной элементарной реакции увеличивается в два—четыре раза.

Уравнение, которое описывает это правило, следующее:

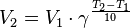
где 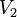— скорость реакции при температуре 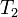, 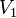— скорость реакции при температуре 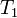, 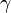— температурный коэффициент реакции (если он равен 2, например, то скорость реакции будет увеличиваться в 2 раза при повышении температуры на 10 градусов).

Изотерма химической реакции (изотерма Вант-Гоффа)При самопроизвольном протекании химической реакции изменение свободной энергии системы отлично от нуля (ΔG < 0, ΔF < 0). Т.о., для самопроизвольного процесса можно записать:

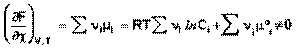(39)

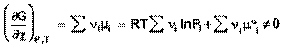(40)

При протекании реакции в большом количестве реакционной смеси, таком, что при превращении n_i молей каждого из компонентов концентрации реагентов С_i практически не изменяются, частную производную свободной энергии Гельмгольца по химической переменной можно заменить равной ей величиной отношения ΔF к Δχ, т.е. принять, что

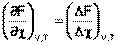
Положив Δχ = 1, получаем

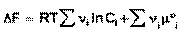(41)

Поскольку, как следует из (35,37), 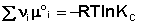, окончательно получаем уравнение, называемое изотермой химической реакции (изотермой Вант-Гоффа):

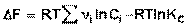(42)

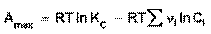(43)

Для изобарно-изотермического процесса аналогичным образом можно получить:

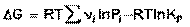(44)

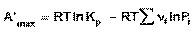(45)

Уравнение изотермы Вант-Гоффа позволяет рассчитать максимальную работу химической реакции и тем самым определить возможность её самопроизвольного протекания в каких-либо конкретных условиях (при температуре Т и концентрациях реагентов C_i или парциальных давлениях P_i).

Вопрос 15