Корпускулярно-волновая двойственность света

Такие явления, как интерференция и дифракция света, убедительно свидетельствуют о волновой природе света. В то же время закономерности равновесного теплового излучения, фотоэффекта и эффекта Комптона можно успешно истолковать с классической точки зрения только на основе представлений о свете, как о потоке дискретных фотонов. Однако волновой и корпускулярный способы описания света не противоречат, а взаимно дополняют друг друга, так как свет одновременно обладает и волновыми и корпускулярными свойствами.

Волновые свойства света играют определяющую роль в закономерностях его интерференции, дифракции, поляризации, а корпускулярные — в процессах взаимодействия света с веществом. Чем больше длина волны света, тем меньше импульс и энергия фотона и тем труднее обнаружить корпускулярные свойства света. Например, внешний фотоэффект происходит только при энергиях фотонов, больших или равных работе выхода электрона из вещества. Чем меньше длина волны электромагнитного излучения, тем больше энергия и импульс фотонов и тем труднее обнаружить волновые свойства этого излучения. Например, рентгеновское излучение дифрагирует только на очень «тонкой» дифракционной решетке — кристаллической решетке твердого тела.

61. Роль прибора при исследовании микрообъектов.

62. Уравнение Шредингера.

Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве и во временичистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона вклассической механике. Его можно назвать уравнением движения квантовой частицы.

Общий случай

В квантовой физике вводится комплекснозначная функция , описывающая чистое состояние объекта, которая называется волновой функцией. В наиболее распространенной копенгагенской интерпретации эта функция связана с вероятностью обнаружения объекта в одном из чистых состояний (квадрат модуля волновой функции представляет собой плотность вероятности). Поведение гамильтоновой системы в чистом состоянии полностью описывается с помощью волновой функции.

Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения в частных физических задачах. Таким уравнением является уравнение Шрёдингера.

Пусть волновая функция задана в N-мерном пространстве, тогда в каждой точке с координатами , в определенный момент времени t она будет иметь вид . В таком случае уравнение Шрёдингера запишется в виде:

где , — постоянная Планка; — масса частицы, — внешняя по отношению к частице потенциальная энергия в точке , — оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:

где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.

63. Частица в потенциальном «ящике».

Потенциальным “ящиком” называют потенциальную яму с вертикальными стенками (рис. 7). Область пространства с координатами от x₁доx₂на рис. 7 и есть потенциальный “ящик”. В реальной действительности такая ситуация наблюдается, например, для электронов в металле: внутри металла они свободны, но чтобы покинуть металл, электроны должны совершить работу выхода А_вых, равную

Рассмотрим простейший пример решения уравнения Шрёдингера для частицы, находящейся в потенциальном ящике с бесконечно высокими стенками (т.е. на границах ящика E_p ® ¥ , рис.8). Это, безусловно, идеализация. В действительности стенки ящика будут всегда конечной высоты. Однако на данной модели наиболее просто показать, что дает решение уравнения Шрёдингера. Итак, рассмотрим одномерный потенциальный ящик с бесконечно высокими стенками (рис.8). Ширина ящика l. Внутри ящика Е_p = 0,т.е. частица свободна. Уравнение Шрёдингера для этого случая примет вид:

Граничные условия: 1) при x = 0 y (0) = 0, 2) при x = l y(l) = 0.

(25)     (26)

Смысл этих условий прост: частица не может находиться на стенках ящика, так как значение Е_p = ¥ не имеет физического смысла.

Условие нормировки:

(27)

Смысл его: частица достоверно находится внутри ящика, т.е. в области координат 0 < x < l.

Уравнения (25) – (27) полностью описывают поставленную задачу.

Решим уравнение (25). Обратите внимание, что по форме оно полностью совпадает с дифференциальным уравнением гармонических колебаний. Следовательно, и решения этих уравнений будут одинаковы:

(28)

Математически задача решена, но физического содержания решение еще не получило. Необходимо, во-первых, определить две произвольные постоянные А и a₀. Значение a₀находим сразу из первого граничного условия: y (0) = 0, откуда a₀= 0. Величину А найдем из условия нормировки, но сделаем это позднее. Осталось неиспользованным второе граничное условие y (l) = 0. Это возможно, если аргумент у синуса кратен p :

(29)

где n = 1, 2, 3 , …¥ . Значение n = 0 лишено физического смысла, так как слева в уравнении (29) ни одна величина не равна нулю. Таким образом, мы пришли к выводу: решение уравнения Шрёдингера имеет физический смысл не при любых значениях энергии, а только при таких, когда выполняется условие (29), т.е. при

(30)

где n = 1, 2, 3, … ¥ . Подставив в уравнение (28) a₀= 0 и получим

(31)

Из условия нормировки пси-функции найдем значение А:

откуда Окончательно имеем набор пси-функций, зависящих от параметра n:

(32)

Вид первых четырех пси-функций представлен на рис. 9.

Величина n характеризует значение энергии частицы и называется квантовым числом, так как энергия принимает дискретные значения, или, как говорят, квантуется.

На рис.10 показано распределение вероятности нахождения частицы в той или иной области ящика при различных значениях квантового числа n.

Подведем итог. Что мы получили в результате решения уравнения Шрёдингера? Во-первых, набор пси-функций, зависящих от квантового числа n. Во-вторых, значения энергии Е, при которых решение уравнения Шрёдингера имеет физический смысл. В-третьих, распределение вероятности обнаружения частицы в различных точках оси xвнутри ящика. Подобные же результаты получаются при решении уравнения Шрёдингера и в других случаях, например, для атома водорода.

Остановимся подробнее на условии (30):

Оно означает, что энергия частицы внутри ящика с бесконечно высокими стенками может принимать не любые значения, а только дискретный ряд значений, пропорциональных квадрату числа n. Иными словами, энергия частицы квантуется. На рис. 11 показаны разрешенные уровни значений энергии Е. Отметим, что Найдем относительное изменение энергии при переходе с одного уровня на соседний:

(33)

Очевидно, что при n ® ¥ т.е. энергия изменяется непрерывно. Это соответствует переходу к классической физике. Кстати, при n® ¥ число максимумов на рис. 10 будет очень велико, они будут располагаться столь тесно, что вероятность будет практически постоянна вдоль оси x, как это и считается в классической физике.

Отметим, что условие квантования мы получили из граничного условия y (l) = 0. Если l ® ¥ , т.е. область движения частицы неограничена, то изменение энергии D Е® 0 (см. уравнение (33)), т.е. энергия изменяется непрерывно, никакого квантования нет. Это еще раз говорит о том, что в макромире квантово-механические эффекты не проявляются, они наблюдаются только в микромире.

Условие квантования энергии имеет простой смысл: на длине ящика должно уложиться целое число длин волн де Бройля. Действительно,

откуда (см. рис.9). Любые другие состояния невозможны.

64. Квантовые числа и периодическая система элементов.

Квантовые числа — энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.

1. Главное квaнтовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1 (n = 1, 2, 3, . . .)

2. Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 до n-1 (l = 0, 1, 2, 3,..., n-1). Каждому значению l соответствует орбиталь особой формы. Орбитали с l = 0 называются s-орбиталями,
l = 1 – р-орбиталями (3 типа, отличающихся магнитным квантовым числом m),
l = 2 – d-орбиталями (5 типов),
l = 3 – f-орбиталями (7 типов).

3. Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. Его значения изменяются от +l до -l, включая 0. Например, при l = 1 число m принимает 3 значения: +1, 0, -1, поэтому существуют 3 типа р-АО: р_x, р_y, р_z.

4. Спиновое квантовое число s может принимать лишь два возможных значения +1/2 и -1/2. Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона, называемогоспином (от англ. веретено). Для обозначения электронов с различными спинами используются символы: и .

65. Радиоактивность. Период полураспада.

Радиоакти́вность (от лат. radius «луч» и āctīvus «действенный») — свойство атомных ядерсамопроизвольно (спонтанно) изменять свой состав (заряд Z, массовое число A) путём испускания элементарных частиц или ядерных фрагментов^[1]. Соответствующее явление называется радиоакти́вным распа́дом. Радиоактивностью называют также свойство вещества, содержащего радиоактивные ядра.

Установлено, что радиоактивны все химические элементы с порядковым номером, большим 82 (то есть начиная с висмута), и многие более лёгкие элементы (прометий и технеций не имеют стабильных изотопов, а у некоторых элементов, таких как индий, калий или кальций, часть природных изотопов стабильны, другие же радиоактивны).

Естественная радиоактивность — самопроизвольный распад ядер элементов, встречающихся в природе.

Искусственная радиоактивность — самопроизвольный распад ядер элементов, полученных искусственным путем через соответствующие ядерные реакции.

Энергетические спектры α-частиц и γ-квантов, излучаемых радиоактивными ядрами, прерывистые («дискретные»), а спектр β-частиц — непрерывный.

Распад, сопровождающийся испусканием альфа-частиц, назвали альфа-распадом; распад, сопровождающийся испусканием бета-частиц, был назван бета-распадом (в настоящее время известно, что существуют типы бета-распада без испускания бета-частиц, однако бета-распад всегда сопровождается испусканием нейтрино или антинейтрино). Термин «гамма-распад» применяется редко; испускание ядром гамма-квантов называют обычно изомерным переходом. Гамма-излучение часто сопровождает другие типы распада.

Закон радиоактивного распада — закон, открытый Фредериком Содди и Эрнестом Резерфордомэкспериментальным путём и сформулированный в 1903 году. Современная формулировка закона:

,

что означает, что число распадов за интервал времени 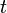в произвольном веществе пропорционально числу имеющихся в образце атомов .

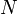В этом математическом выражении — постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени и имеющая размерность с⁻¹. Знак минус указывает на убыль числа радиоактивных ядер со временем.

Этот закон считается основным законом радиоактивности, из него было извлечено несколько важных следствий, среди которых формулировки характеристик распада — среднее время жизни атома и период полураспада