Третий закон Кеплера (гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

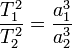, где T₁ и T₂ — периоды обращения двух планет вокруг Солнца, а a₁ и a₂ — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты: 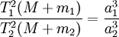, где M — масса Солнца, а m₁ и m₂ — массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Второй закон Кеплера утверждает, что радиус-вектор обращающегося тела заметает равные площади за равные промежутки времени. Если теперь мы возьмём очень малые промежутки времени в момент, когда планета находится в точках A и B (перигелий иафелий), то мы сможем аппроксимировать площадь треугольниками с высотами, равными расстоянию от планеты до Солнца, и основанием, равным произведению скорости планеты на время.

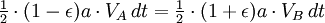
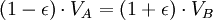
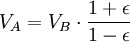
Используя закон сохранения энергии для полной энергии планеты в точках A и B, запишем

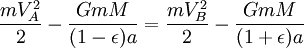
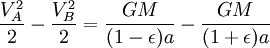
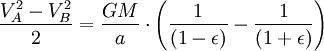
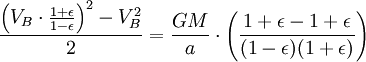
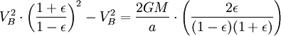
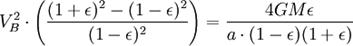
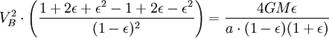
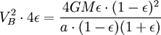
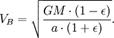
Теперь, когда мы нашли V_B, мы можем найти секториальную скорость. Так как она постоянна, то можем выбрать любую точку эллипса: например, для точки B получим

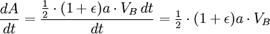
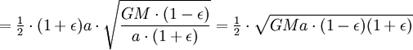
Однако полная площадь эллипса равна 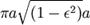(что равно πab, поскольку 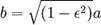). Время полного оборота, таким образом, равно

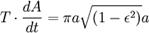
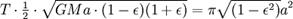
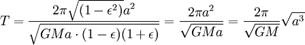
Заметим, что если масса m не пренебрежимо мала по сравнению с M, то планета будет обращаться вокруг Солнца с той же скоростью и по той же орбите, что и материальная точка, обращающаяся вокруг массы M + m (см. приведённая масса). При этом массу M в последней формуле нужно заменить на M + m:

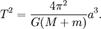
13. Взаимосвязь между свойствами Вселенной и возможностью появления в ней разумной жизни.

Дальнейшее развитие этих идей позволило установить еще более глубокую связь между фундаментальными свойствами Вселенной в целом и наличием в ней жизни (и человека). Необходимость такой связи ясно осознавал еще К. Э. Циолковский. «Тот космос, который мы знаем, — писал он, — не может быть иным», поскольку человеческое существование не случайно, а имманентно космосу. В работах Идлиса и Зельманова эта идея была наполнена конкретным астрономическим содержанием. Речь шла о наблюдаемых астрономических свойствах Вселенной, и обнаруженная связь относилась к наблюдаемой области Вселенной. В дальнейшем эта связь была распространена как на наблюдаемые, так и на теоретические свойства Вселенной в целом, а не только ее наблюдаемой части. И (что особенно важно!), оказалось, — не только астрономические свойства Вселенной, но и фундаментальные физические параметры материального мира тесно связаны с наличием во Вселенной жизни и человека.

Рассмотрим вначале астрономические свойства Вселенной. Одним из важнейших астрономических свойств является средняя плотность вещества во Вселенной. Как мы видели в предыдущей главе, средняя плотность близка к критической, и это находит объяснение в рамках инфляционной модели Вселенной. Любопытно однако то, что в обитаемой вселенной и не могло быть иначе. Действительно, если средняя плотность вещества много меньше критической, то тормозящее действие гравитации мало — Вселенная расширяется очень быстро, и при такой скорости в ней не могут сформироваться гравитационно связанные системы — галактики, звезды, планеты, которые необходимы для возникновения жизни. С другой стороны, если средняя плотность много больше критической, то тормозящее действие гравитации очень велико, расширение быстро сменяется сжатием, и время жизни такой Вселенной (длительность цикла расширения-сжатия) оказывается слишком мало, много меньше, чем требуется для возникновения жизни и тем более эволюции ее до стадии человека. Таким образом, в обитаемой Вселенной средняя плотность вещества должна быть близка к критической. Тогда скорость расширения будет не столь велика, и во Вселенной смогут сформироваться звезды и планеты. В то же время длительность стадии расширения будет достаточна для возникновения и эволюции жизни.
С критической плотностью связана изотропия Вселенной — важнейшее свойство, которое постулировалось в модели Фридмана и которое получило экспериментальное подтверждение в наблюдаемой изотропии реликтового излучения. Возникает, однако, вопрос: как объяснить это свойство Вселенной? Можно ли, не постулируя, вывести это свойство теоретически? С. Хокинг показал, что наблюдаемую изотропию можно объяснить в том случае, если плотность вещества с большой точностью совпадает с критической. Но так как это условие связано с существованием жизни во Вселенной, то и изотропия также оказывается связана с жизнью. То есть обитаемая Вселенная с необходимостью должна быть изотропной.
Перейдем теперь к такой фундаментальной характеристике Вселенной, как размерность физического пространства. Почему физическое пространство трехмерно? Прежде всего человек сам трехмерное существо, поэтому он не может существовать в пространстве одного или двух измерений. Предположим, существуют какие-то одномерные или двумерные миры. Мы могли бы мысленно изучать их свойства, но жить в этих мирах, наблюдать их изнутри мы не можем. Возможно, какие-то экзотические (с нашей точки зрения) одномерные и двумерные существа могут обитать в этих мирах. Но человек обитать в них не может. Наша Вселенная не может быть ни одномерной, ни двумерной. Но остается еще много других возможностей. Ведь пространство могло бы иметь больше трех измерений. Почему же тогда физическое пространство трехмерно, а например, не пятимерио? Чтобы ответить на этот вопрос, посмотрим, как видоизменяются физические законы с изменением размерности пространства.

В нашем трехмерном мире сила взаимодействия двух электрических зарядов убывает обратно пропорционально квадрату расстояния между ними (закон Кулона). То же самое относится к силе взаимодействия двух тяготеющих масс (закон всемирного тяготения). Как связан закон обратных квадратов с размерностью пространства? Напряженность поля, или сила, действующая на пробный заряд в данной точке, на расстоянии г от заряда, создающего поле, определяется плотностью силовых линий, т. е. числом линий, проходящих через единицу поверхности в точке наблюдения.

Анализ движения тел под действием такой силы был выполнен П. Эренфестом в 1917 г. Если мы рассмотрим, например, планету и Солнце в 4-мерном пространстве (а также в пространстве большего числа измерений), то планета в гаком пространстве не будет вращаться вокруг Солнца по устойчивой круговой (или эллиптической) орбите: она либо упадет на Солнце, либо уйдет в бесконечность. Значит, в таких мирах не существует аналогов планетных систем и атомов. А следовательно, в них не может существовать жизнь, построенная на молекулярном уровне. Какие-то гипотетические «полевые» формы жизни могли бы существовать в таком мире, но человек «из плоти и крови», человек в его физическом теле, состоящем из сложных органических молекул, не может существовать в пространстве более чем трех измерений. Казалось бы, увеличение размерности пространства должно открыть новые возможности для построения все более сложных структурных образований атомной природы. Но выяснилось, что это не так.

С другой стороны, при N = 1, 2 сила взаимодействия падает с расстоянием слишком медленно. Поэтому какую бы скорость ни придать заряду, он не сможет уйти из поля притяжения центрального тела, он как бы находится в глубокой (бесконечно глубокой) потенциальной яме, и чтобы извлечь его оттуда, надо затратить бесконечно большую энергию. Следовательно, в таком пространстве не существовало бы свободного движения тяготеющих масс, и в его («одномерных» или «двумерных») атомах не могли бы происходить процессы ионизации. В таком мире не существовали бы процессы возникновения и распада, процессы обмена, характерные для жизни. Только в трехмерном мире возможно возникновение сложных молекулярных структур, обладающих способностью к обмену, изменчивости, эволюции.

Понятно теперь, почему мы живем в трехмерном мире: в другом мире мы просто не могли бы существовать. Это относится не только к человеку, но и к любому разумному существу с телом, представляющим собой сложную структуру, построенную из атомов.
14. Понятие времени. Измерение коротких и длинных временных промежутков.

Вре́мя — одно из основных понятий физики и философии, условная сравнительная мера движения материи, а также одна из координат пространства-времени, вдоль которой протянуты мировые линиифизических тел .

15. Понятие пространства. Измерение больших и малых расстояний.

В физике пространством называют ту «арену действий», на которой разворачиваются физические процессы и явления и которую мы субъективно ощущаем как «вместилище предметов».

В физике часто используются многомерные пространства — например, фазовое пространство, в котором состояние сложной системы объектов представляется одной точкой. Такие пространства — не более чем абстракции, предназначенные для постановки и решения вполне «земных» задач в обыкновенном трёхмерном пространстве.

В теории относительности пространство оказывается одним из проявлений единого пространства-времени, и деление отдельно на пространство и время становится зависящим от конкретной системы отсчёта.

В большинстве разделов физики сами свойства физического пространства (размерность, неограниченность и т. п.) никак не зависят от присутствия или отсутствия материальных тел. В общей теории относительности оказывается, что материальные тела модифицируют свойства пространства, а точнее, пространства-времени, «искривляют» пространство-время.

Одним из постулатов любой физической теории (Ньютона, ОТО и т. д.) является постулат о реальности того или иного математического пространства (например Евклидова у Ньютона).

16. Детерминизм Лапласа.

Детермини́зм (лат. determinare — определять, ограничивать) — философское учение об объективной закономерной взаимосвязи и взаимообусловленности явлений материального и духовного мира.

Детерминизм в науке.

1) Всё определено в этом мире, и ничто не в состоянии этого изменить.

2) Всякое действие вызывает следствие подобно всему тому, что происходит в этой жизни.

На принципе детерминизма построена вся классическая физика, за исключением термодинамики и молекулярной физики. Детерминизм подразумевает выполнение обратимости времени, то есть частица придёт в исходное состояние, если обратить время. Каждая траектория единственным образом определяется начальными условиями. Всё это находится в замечательном согласии с экспериментальными данными макромира.

Лаплас: "Дайте знать начальное состояние частицы, и я предреку то, в какое она придет через некоторое время, поскольку все в этом мире предопределено и процессы можно предсказать"
17. Макроскопическое и микроскопическое описание систем, состоящих из большого числа частиц.

18. Распределение Максвелла.

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике ихимии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.

Во многих других случаях, однако, даже приблизительно не выполнено условие доминирования упругих соударений над всеми другими процессами. Это верно, например, в физике ионосферы и космической плазмы, где процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы) имеют большое значение, в особенности для электронов. Предположение о применимости распределения Максвелла дало бы в этом случае не только количественно неверные результаты, но даже предотвратило бы правильное понимание физики процессов на качественном уровне. Также, в том случае где квантовая де Бройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, будут наблюдаться отклонения от распределения Максвелла из-за квантовых эффектов.

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

,

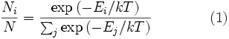где 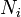является числом молекул имеющих энергию 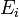при температуре системы 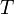, 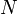является общим числом молекул в системе и 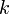— постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем 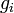, обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма.

19. Необратимые и обратимые процессы. Открытые, закрытые и изолированные системы.

Обратимый процесс (то есть равновесный) — термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений.

Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину.

Обратимые процессы дают наибольшую работу. Бо́льшую работу от системы вообще получить невозможно. Это придает обратимым процессам теоретическую важность. На практике обратимый процесс реализовать невозможно. Он протекает бесконечно медленно, и можно только приблизиться к нему.

Следует отметить, что термодинамическая обратимость процесса отличается от химической обратимости. Химическая обратимость характеризует направление процесса, а термодинамическая — способ его проведения.

Понятия равновесного состояния и обратимого процесса играют большую роль в термодинамике. Все количественные выводы термодинамики применимы только к равновесным состояниям и обратимым процессам

20. Энтропия в изолированных и не изолированных системах.

Откры́тая систе́ма:

§ В физике — система, обменивающаяся веществом, энергией и информацией с внешним, по отношению к системе, миром, в отличие от закрытой системы, у которой отсутствует какой-либо обмен материей с окружающей средой. В термодинамике c закрытой,изолированной и замкнутой системами тесно связано явление возрастания энтропии.

Закрытая система — частично изолированная система, у которой отсутствует какой-либо обмен материей с окружающей средой. В полностью изолированной системе дополнительно отсутствует обмен энергией, а в замкнутой системе — отсутствует ещё и обмен информацией.

В термодинамике закрытая система может обмениваться со своим окружением только энергией, в частности теплотой, тогда как воткрытой системе возможен обмен и веществом и энергией. Для закрытых систем характерно увеличение беспорядка

Изолированная система — система, которая не обменивается с окружающей средой ни веществом, ни энергией.