Электромагнитные волны. вектор умова

1. Связанные между собою переменные электрическое и магнитное поле образуют электромагнитное поле.

Распространяющееся в пространстве ЭМ поле представляет собой ЭМ волну. В отличие от механических волн ЭМ волна может распространяться и в вакууме.

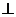
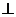
ЭМ волна поперечная, . Напряженность ЭП и напряженность МП колеблются в одинаковой фазе (синхронно).

Уравнение бегущей ЭМ волны: , где x – расстояние от данной точки до источника волн, V- скорость распространения волны. По Максвеллу , а в вакууме , т.е. совпадает со скоростью распространения света в вакууме. Вывод: свет – это электромагнитная волна.

2. Энергия, переносимая ЭМ волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны, называется плотностью потока энергии или вектором Умова – Пойнтинга

- № 92, 312, 376

УРАВНЕНИЕ МАКСВЕЛЛА

1. Теорема Остроградского–Гаусса: или Физический смысл: источником электростатического поля являются электрические заряды.

2. Теорема Остроградского – Гаусса для магнитного поля: Физический смысл: в природе не существует магнитных зарядов (линии напряженности МП замкнуты).

3. Циркуляция вектора напряженности электростатического поля

Физический смысл: работа перемещения заряда по замкнутому контуру в электростатическом поле равна нулю.

4. Ранее был получен закон полного тока – циркуляция вектора напряженности МП по замкнутому контуру .

Однако МП создается не только токами в проводниках, но и переменным ЭП. Переменное ЭП получило название тока смещения , где - поток электрической индукции. Т.о.закон полного тока примет вид или

5. В законе ЭМ индукции , где d – изменение магнитного потока через замкнутый контур. Но изменение магнитного потока может происходить и в постоянном МП, например, при изменении площади контура или его ориентации в пространстве ( = S cos ).

В законе ЭМ индукции Максвелл заменил полную производную частной производной . Это означает, что изменение магнитного потока происходит из-за того, что МП является переменным (изменяется ).

Итак, или учитывая, что э.д.с. , а = ( d ) имеем , здесь - напряженность поля сторонних сил.

- № 91, 309, 500

ФОТОМЕТРИЯ

1. Поток лучистой энергии - энергия, протекающая через площадку за единицу времени, измеряется в люменах – лм.

2. Сила света J - поток энергии, приходящийся на единицу телесного угла, измеряется в канделах – кд.

Для изотропного источника J= /4

3. Освещенность - поток энергии, падающий на единицу поверхности, измеряется в люксах – лк.

4. Яркость источника - поток энергии, направляемый единицей светящейся поверхности внутрь единичного телесного угла, измеряется в канделла/кв.м.

5. Светимость S – суммарный поток энергии, посылаемый единицей светящейся поверхности по всем направлениям, измеряется в люмен/м².

Между и S есть связь: S=

6. Для точечного источника света = cos i, где r - расстояние от источника, i - угол между падающим лугом и нормалью к площадке.

- № 46

ГЕОМЕТРИЧЕСКАЯ ОПТИКА

1. Закон прямолинейного распространения света – в оптически однородной среде (показатель преломления во всех точках одинаков) свет распространяется по прямой линии.

2. Закон отражения света: а) луч падающий, отраженный луч и перпендикуляр к границе раздела сред в точке падения лежат в одной плоскости; б) угол падения равен углу отражения (углы отсчитываются от перпендикуляра).

3. Закон преломления света: а) луч падающий, преломленный луч и перпендикуляр к границе раздела сред в точке падения луча лежат в одной плоскости; б) = , n₁, n₂ – показатели преломления сред, показывающие во сколько раз скорость света в данной среде меньше, чем в вакууме.

4. Если n₂>n, то i > ; если n₂<n, то i < ;

При некотором i_пр угол преломления = , т.е. преломленный луч не проходит во вторую среду и скользит по поверхности раздела сред: Sin i_пр=

Это явление называется полным внутренним отражением.

5. Оптическая длина пути – произведение геометрической длины светового пучка на показатель преломления - l·n.

6. Принцип Ферма: в оптически неоднородной среде свет распространяется по траектории, оптическая длина которой экстремальна (максимальна или минимальна, или стационарна).

ЛИНЗЫ

1. Линзы – прозрачные для света тела, ограниченные сферическими поверхностями (одна поверхность может быть и плоской).

2. Оптическая сила линзы D= , где n_вещ – показатель преломления вещества линзы, n_ср – показатель преломления среды, в которой находится линза, R₁ и R₂ – радиусы сферических поверхностей. D измеряется в диоптриях (дптр), а радиусы в метрах.

Если D>0, то линза называется собирающей, если D<0, то рассеивающей.

Радиус сферической поверхности считается положительным, если ее центр находится справа от линзы (по ходу падающего луча) и отрицательным, если центр находится слева.

3. Фокусное расстояние линзы F= , фокусы располагаются симметрично по обе стороны линзы.

4. Главная оптическая ось – линия, проходящая через центр линзы и центры сферических поверхностей (только одна), побочная оптическая ось – линия проходящая через центр линзы (их много).

5. Фокальная плоскость – плоскость, проходящая через фокус перпендикулярно главной оптической оси.

6. В общем случае луч света, проходящий через линзу преломляется (изменяет свое направление)

а) для собирающей линзы:

- луч света, проходящий через центр линзы, не преломляется;

- луч света, падающий на линзу параллельно главной оптической оси,

после преломления проходит через фокус линзы;

- луч света, падающий на линзу произвольно, после преломления

проходит через точку пересечения фокальной плоскости с побочной

оптической осью, параллельной падающему лучу.

б) для рассеивающей линзы:

- луч света, проходящий через центр линзы, не преломляется;

- луч света, падающий на линзу параллельно главной оптической оси,

преломляется таким образом, чтобы его продолжение в обратную

сторону проходило через фокус линзы (расположенный слева от

линзы);

- луч света, падающий на линзу произвольно, преломляется так, что

продолжение преломленного луча в обратную сторону проходит

через точку пересечения фокальной плоскости (расположенной слева

от линзы) и побочной оптической оси, параллельной падающему

лучу.

7. Изображение называется действительным, если оно получается при пересечении преломленных лучей. В противном случае изображение называется мнимым (пересечение продолжений преломленных лучей в обратную сторону). Рассеивающая линза всегда дает мнимое изображение, а собирающая как действительное, так и мнимое в зависимости от того, как расположен предмет относительно линзы.

8. Расстояние наилучшего зрения – расстояние, на котором предмет виден наиболее отчетливо. Для нормального глаза оно равно 25 см.

9. Лупа – короткофокусная собирающая линза. Увеличение, даваемой лупой 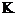= , где F – фокусное расстояние лупы в метрах.

10. Формула линзы: - + = , где а₁ – расстояние от линзы до предмета, а₂ – расстояние от линзы до изображения.

Расстояния, отсчитываемые от линзы в направлении падающего луча, считаются положительными, а, отсчитываемые от линзы против хода падающего луча – отрицательными.

- № 69, 95, 143, 144, 170, 182, 219, 356, 391

ЗЕРКАЛА

1. Системы, отражающие падающие на них свет, называется зеркалами. В зависимости от формы отражающей поверхности зеркала бывают плоские, сферические, параболические и т.д. Ниже будут рассмотрены сферические зеркала.

2. Линия, проходящая через вершину зеркала и центр сферической поверхности, называется оптической осью. Фокусное расстояние зеркала F= , где R - радиус сферической поверхности. Фокус располагается посередине между центром сферической поверхности и вершиной зеркала.

3. Зеркала бывают выпуклые и вогнутые (по отношению к падающему лучу света).

а) для вогнутого зеркала:

- луч света, падающий параллельно оптической оси, после отражения,

проходит через фокус;

- луч света, при падении проходящий через фокус, после отражения

идет параллельно оптической оси.

б) для выпуклого зеркала:

- луч света, падающий параллельно оптической оси, отражается так,

что его продолжение в обратную сторону проходит через фокус;

- луч света, падающий на зеркало так, что его продолжение проходит

через фокус (за зеркалом), отражается параллельно оптической оси.

4. Формула зеркала: + = , где а и b – расстояния от зеркала до предмета и от зеркала до изображения, F – фокусное расстояние.

Для вогнутого зеркала все величины положительные, для выпуклого зеркала а отрицательно, а b и F положительны.

- № 144, 391

ИНТЕРФЕРЕНЦИЯ СВЕТА

1. Когерентные волны – волны, в которых колебания совершаются с одинаковой частотой в одном направлении и с постоянной разностью фаз.

2. Интерференция – результат наложения когерентных волн, приводящий либо к усилению, либо к ослаблению налагаемых волн.

3. Амплитуда результирующей волны при интерференции , где ₁, ₂ – амплитуды складывающихся волн, ( - ) – разность фаз волн.

Условие max (усиление волн): - =2n , n=0, 1, 2..., условие min (ослабление волн): - =(2n-1) , n=1, 2, 3...

4. Условия max и min можно выразить и через разность хода волн: 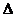S=2n (max), n=0, 1, …; 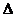S=(2n-1) , n=1, 2, ..., где - длина волны.

5. Опыт Юнга

S₁, S₂ – когерентные источники света, Э – экран, - точка, где налагаются волны.

В точке будет max, если y= , где n=0, 1, 2… и min, если y = , где n=1, 2, …

6. При отражении света от плоской пластины (верхней и нижней граней) разность хода волн зависит от угла падения света i и толщины пластины d.

Примером интерференции света при одинаковом i, но при разных d являются кольца Ньютона.

Радиус светлого кольца = , n=1, 2, ..., а темного r = , n=0, 1, ..., R – радиус кривизны линзы.

7. В случае освещения белым светом, поверхность масляной пленки на поверхности воды окажется цветной – пример интерференции.

- № 45, 118, 172, 245, 269, 272, 450, 482

ДИФРАКЦИЯ СВЕТА

1. Дифракция - отклонение от прямолинейного распространения света, выражающееся в огибании препятствий и отверстий (размеры препятствий и отверстий должны быть сравнимы с длиной волны).

2. Волновая поверхность – геометрическое место точек среды, колеблющихся в одинаковой фазе. По виду волновых поверхностей различают сферические и плоские волны.

3. Принцип Гюйгенса-Френеля: 1) каждую точку волновой поверхности, до которой дошла волна, можно рассматривать как источник вторичных волн; 2) вторичные волны когерентные, поэтому должны интерферировать.

4. Зоны Френеля – участки волновой поверхности, выбираемые таким образом, чтобы от соседних зон Френеля разность хода волн до данной точки составляла половину длины волны ( ).

5. Пусть свет падает на экран с отверстием радиусом . Число зон Френеля, укладываемых на отверстии, в случае сферических волн i= , где R – радиус волновой поверхности (расстояние от источника до экрана с отверстием), r₀ – расстояние от отверстия до экрана, на который падает свет после прохождения отверстия.

В случае плоской волны (R= 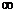) число зон i=

6. Условие max, если число зон i нечетное, если число зон i четное, условие min.

Радиус i-й зоны Френеля =

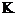7. В случае дифракции на одной щели шириной а для плоских волн: аSin =(2 ) , =1, 2, …- условие max

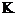
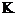аSin =2 , =1, 2, ... – условие min

При =0 выполняется условие max

8. Для дифракционной решетки с d=a+b

условие max: dSin = , 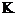=0, 1, 2, ...

условие min: aSin =m , m=1, 2, ...

- № 20, 94, 119, 169, 194, 218, 244, 254, 290, 328, 368, 378, 504

ПОЛЯРИЗАЦИЯ СВЕТА

1. Свет – распространяющаяся в пространстве э.м.волна, волна поперечная. За направление колебаний принимается направление вектора напряженности электрического поля (которое 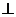направлению распространения волны).

2. Свет называется поляризованным, если вектор колеблется в строго определенной плоскости.

3. Свет называется естественным, если вектор лежит во всевозможных плоскостях (но 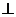направлению распространения света).

4. Свет называется частично поляризованным, если вектор лежит преимущественно в одной плоскости.

5. Свет, испускаемый естественными источниками, является не поляризованным, т.е. естественным.

6. При отражении естественного света от границы раздела двух сред отраженный и преломленный лучи становятся частично поляризованными.

7. Если луч света падает под углом Брюстера i₀, то отраженный луч является полностью поляризованным (а преломленный луч – частично поляризованным).

Угол Брюстера отвечает условию: tg i₀=

8. Если луч света падает под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны.

9. Кристалл, показатель преломления которого в различных направлениях различен, называется оптически анизотропным. При падении естественного света на анизотропный кристалл он расщепляется на 2 луча – обыкновенный и необыкновенный – явление называется двойным лучепреломлением. Обыкновенный луч подчиняется закону преломления света, а необыкновенный – не подчиняется.

10. Обыкновенный и необыкновенный лучи поляризованы во взаимно перпендикулярных плоскостях.

11. В анизотропном кристалле имеется направление, вдоль которого оба луча распространяются с одинаковой скоростью не раздваиваясь, т.е. не наблюдается двойное лучепреломление. Такое направление в кристалле называется оптической осью кристалла. Плоскость, содержащая оптическую ось и данный луч, называется главной плоскостью или главным сечением для данного луча.

12. Обыкновенный луч поляризован в главной плоскости, а необыкновенный в плоскости, перпендикулярной главной плоскости.

13. Если на анизотропный кристалл падает поляризованный свет, то при выходе из него плоскость поляризации поворачивается на некоторый угол, величина которого пропорциональна толщине кристалла.

При этом интенсивность прошедшего через кристалл света J=J₀Cos² , где J₀ – интенсивность падающего света, а - угол, на который поворачивается плоскость поляризации. Данная формула называется законом Малюса.

14. Закон Малюса выполняется и в случае, когда естественный луч проходит через 2 последовательных анизотропных кристалла, при этом под нужно понимать угол между оптическими осями кристаллов.

При = свет полностью тушится, если второй кристалл вращать вокруг падающего луча, то интенсивность прошедшего света будет меняться от нуля до максимума.

15. Рассмотренные поляризованные лучи называются линейно-поляризованными. Существуют также лучи с эллиптической поляризацией (частный случай круговая поляризация).

Свет называется эллиптически поляризованным, если конец вектора напряженности электрического поля описывает эллипс (в частном случае окружность).

Такой свет является результатом интерференции поляризованных волн, плоскости поляризаций которых взаимно перпендикулярны.

- № 8, 140, 264, 314, 330, 344, 418