Вынужденные колебания. резонанс

При наличии сил сопротивления, чтобы колебания были незатухающими необходимо приложить к телу периодически изменяющуюся внешнюю силу – вынуждающую силу 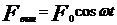, где F₀ – амплитудное значение (max) значение F_вын, ω - циклическая частота вынуждающей силы.

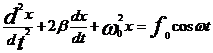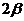Уравнение, описывающее вынужденные колебания: , где и 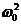такие же, как при затухающих колебаниях, а .

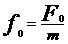Решение этого уравнения имеет вид: 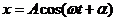, т.е. вынужденные колебания совершаются с частотой, равной частоте вынуждающей силы.

Амплитуда вынужденных колебаний 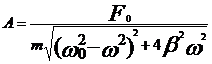зависит от частоты вынуждающей силы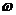

Графически эта зависимость выглядит так:

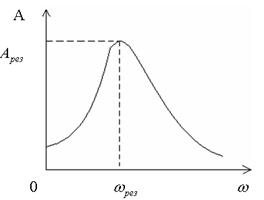
Частота, при которой = max, называется резонансной _рез

Явление, при котором амплитуда колебаний достигает max, называется резонансом.

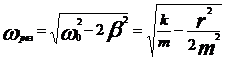
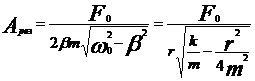- max

- № 156, 480

ВОЛНЫ. БЕГУЩИЕ ВОЛНЫ

1. Волны – распространяющиеся в среде колебания. Частица среды, находящаяся на расстоянии S от источника волн, совершает колебания по закону

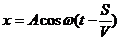– уравнение бегущей волны, 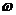- частота колебаний, V - скорость распространения волны. Напомним, что 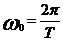, 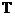– период колебаний

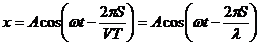, где 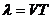- длина волны; 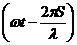– фаза; 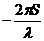– начальная фаза.

2. Фронт волны – геометрическое место точек среды, до которых дошла волна в данный момент времени

Волновая поверхность – геометрическое место точек среды, колеблющихся в одинаковой фазе.

По виду волновой поверхности различают плоские и сферические волны.

Волна называется продольной, если направление колебаний в волне совпадает с направлением распространения волны. Волна называется поперечной, если колебания совершаются в направлении перпендикулярном направлению распространения волны.

3. Когерентные волны – волны, в которых колебания совершаются с одинаковой частотой и в одинаковом направлении, а разность фаз постоянна.

В результате наложения когерентных волн наблюдается интерференция (усиление или ослабление волн)

4. Амплитуда результирующей волны при интерференции 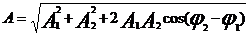, где ₁ и ₂ – амплитуды налагаемых волн, ( ₂ - ₁) – разность фаз волн.

Если ( ₂ - ₁) = 2 nπ, где n= 0, 1, 2..., то = ₁ + ₂, если ( ₂ - ₁) = (2n – 1)π, где n= 1, 2..., то = ₁ - ₂, Первое условие называется условием max, а второе – условием min.

Учитывая, что начальная фаза 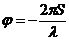, для разности фаз 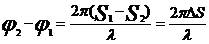, где 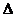S – разность хода волн.

Условия max и min можно выразить через 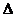S.

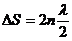– условие max, n=0, 1, 2

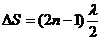– условие min, n=1, 2

- № 19, 68, 70, 263, 331, 416, 481

СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ ОДИНАКОВОЙ ЧАСТОТЫ

Пусть точка участвует одновременно в двух взаимно перпендикулярных колебаниях одинаковой частоты, но с различными амплитудами и начальными фазам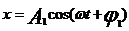и и .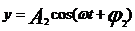

Общее уравнение траектории движения точки имеет вид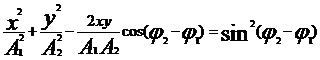

Это общее уравнение эллипса, наклон осей которого зависит от разности фаз ( ₂ - ₁).

Так, при 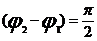, получим обычное уравнение эллипса 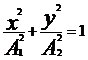, где ₁ и ₂ - полуоси эллипса.

Если амплитуды колебаний одинаковы ₁= ₂ = , то траекторией движения будет окружность: x² + y² = ²

- № 90

ГИДРОСТАТИКА

1. Закон Паскаля – давление, оказываемой на жидкость передается по всем направлениям одинаково.

2. Гидростатическое давление – давление, оказываемой жидкостью вследствие силы тяжести.

На глубине h под поверхностью жидкости давление равно 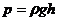, ρ- плотность жидкости.

3. Закон Архимеда: на тело, погруженное в жидкость действует выталкивающая сила, равная весу вытесненной жидкости

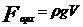, V. – объем вытесненной жидкости

4. Условие плавания тела ρ_T < ρ_Ж, ρ_T и ρ_Ж – плотности тела и жидкости.

ГИДРОДИНАМИКА

1. Идеальная жидкость – несжимаемая жидкость, лишенная вязкости (внутреннего трения).

2. Уравнение неразрывности потока жидкости SV=Const, S – площадь поперечного сечения, V – скорость течения жидкости в данном сечении.

3. Ламинарное течение жидкости – течение жидкости параллельными слоями (траектории частиц жидкости не пересекаются).

4. При турбулентном течении траектории частиц и их скорости хаотично изменяются, движение частиц носит вихревой характер.

5. Уравнение Бернулли для ламинарного течения идеальной жидкости 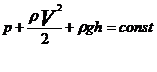, где 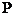– статическое давление, ρqh – гидростатическое давление, 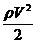– динамическое давление (напор).

6. Сила внутреннего трения между слоями текущей жидкости 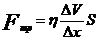, где 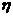– коэффициент вязкости жидкости, S – площадь соприкасающихся слоев, 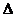V - разность скоростей течения жидкости в слоях, отстоящих друг от друга на расстоянии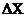

7. Сила сопротивления при движении в жидкости тела сферической формы – формула Стокса

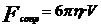, r – радиус шара, V – его скорость.

8. В общем случае сила сопротивления при движении в жидкости (газе) имеет составляющую параллельную направлению движения тела (лобовое сопротивление) и перпендикулярную составляющую (подъемная сила).

9. Формула Пуазейля определяет объем жидкости, протекающий через трубку радиусом R и длиной 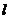за время t

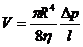, где 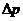– разность давлений на концах трубки

- № 109, 424, 487