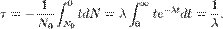Законы радиоактивных распадов.

Закон радиоактивного распада — физический закон, описывающий зависимость интенсивности радиоактивного распада от времени и количества радиоактивных атомов в образце. Открыт Фредериком Содди и Эрнестом Резерфордом, каждый из которых впоследствии был награжден Нобелевской премией. Они обнаружили егоэкспериментальным путём и опубликовали в 1903 году в работах «Сравнительное изучение радиоактивности радия и тория»^[1] и «Радиоактивное превращение»^[2], сформулировав следующим образом^[3]:

Во всех случаях, когда отделяли один из радиоактивных продуктов и исследовали его активность независимо от радиоактивности вещества, из которого он образовался, было обнаружено, что активность при всех исследованиях уменьшается со временем по закону геометрической прогрессии.

из чего с помощью теоремы Бернулли учёные сделали вывод

Скорость превращения всё время пропорциональна количеству систем, еще не подвергнувшихся превращению.

Существует несколько формулировок закона, например, в виде дифференциального уравнения:

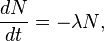
которое означает, что число распадов −dN, произошедшее за короткий интервал времениdt, пропорционально числу атомов N в образце.

Экспоненциальный закон

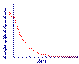
Экспоненциальная кривая радиоактивного распада: по оси абсцисс («оси x») — время, по оси ординат («оси y») — количество нераспавшихся ядер или скорость распада в единицу времени.

В указанном выше математическом выражении 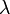— постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени и имеющая размерность с⁻¹. Знак минус указывает на убыль числа радиоактивных ядер со временем.

Решение этого дифференциального уравнения имеет вид:

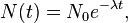
где 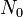— начальное число атомов, то есть число атомов для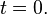

Таким образом, число радиоактивных атомов уменьшается со временем поэкспоненциальному закону. Скорость распада, то есть число распадов в единицу времени 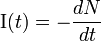, также падает экспоненциально. Дифференцируя выражение для зависимости числа атомов от времени, получаем:

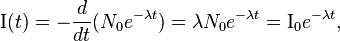
где 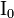— скорость распада в начальный момент времени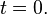

Таким образом, зависимость от времени числа нераспавшихся радиоактивных атомов и скорости распада описывается одной и той же постоянной 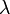^[4][5][6][7].

Характеристики распада

Кроме константы распада 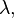радиоактивный распад характеризуют ещё двумя производными от неё константами, рассмотренными ниже.

Среднее время жизни

Из закона радиоактивного распада можно получить выражение для среднего времени жизни радиоактивного атома. Число атомов, в момент времени 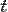претерпевших распад в пределах интервала 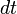равно 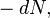их время жизни равно 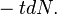Среднее время жизни получаем интегрированием по всему периоду распада: