Свободные колебания в колебательном контуре. Дифференцальное уравнение затухающих электромагнитных колебаний.

КОЛЕБАТЕЛЬНЫМ КОНТУРОМ называется замкнутая цепь, содержащая катушку индуктивности с индуктивностью L и конденсатор с емкостью С. Если в цепи нет активного сопротивления R (резистора), то в контуре возможны гармонические (незатухающие) колебания тока I, заряда конденсатора q и напряжения на элементах.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных затухающих колебаний

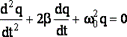
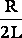
где b = -коэффициент затухания.

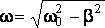
Его решение q(t) = qv0 е-bt cos(wt + a), где

Переменный ток. Полное и индуктивное сопротивление.

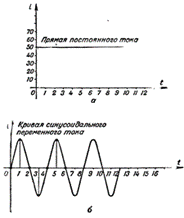Это электрический ток, который периодически изменяется по модулю и направлению.

Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.

В устройствах-потребителях постоянного тока переменный ток часто преобразуется выпрямителями для получения постоянного тока.

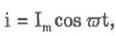
Полное сопротивление (Z) - это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.

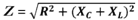
полное сопротивление цепи.

индуктивное сопротивление - это сопротивление проводника, включенного в цепь переменного тока и неимеющего заметного активного сопротивления и емкости, но имеющий заметную индуктивность L.

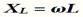
- индуктивное сопротивление проводника переменному току. Где: омега- частота, L- индуктивность (Гн)

Мощность выделяемая в цепи переменного тока, принцип действия теплового амперметра.

мгновенное значение мощности переменного тока, которое равно произведению мгновенных значений напряжения и силы тока:

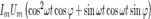
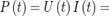
где U(t)=Umcosωt, I(t)=Imcos(ωt-φ) .

Средняя мощность, выделяемая в цепи переменного тока

Тепловой амперметр

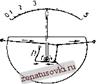Тепловой амперметр основанный на свойстве тока нагревать провода, устроен так: к двум неподвижным зажимам присоединена тонкая проволока. Эта проволока оттянута книзу шелковой нитью, связанной с пружиной. По пути Эта нить петлей охватывает подвижную ось, на которой укреплена стрелка.

Измеряемый ток подводится к неподвижным зажима.м и проходит через проволоку (путь тока показан стрелками). Под действием тока проволока немного нагреется. От нагревания она чуть-чуть удлинится, и шелковая нить, np i-Крепленная к проволоке, оттянется пружинкой. Движение Нити повернет ось и сидящую на ней стрелку.

По отклонению стрелки и определяют величину тока: чем больше ток, тем больше нагревается нить, тем больше поворачивается стрелка.

20. Введение в теорию волновых процессов, основные понятия. Математическое описание синусоидальной волны. Волновое уравнение.

Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры.

В связи с этим волновой процесс может иметь самую разную физическую природу: механическую, химическую (реакция Белоусова — Жаботинского, протекающая в автоколебательном режиме каталитического окисления различных восстановителей бромисто-водородной кислотой HBrO3 ), электромагнитную (электромагнитное излучение), гравитационную (гравитационные волны), спиновую (магнон), плотности вероятности (ток вероятности) и т. д.

Многообразие волновых процессов приводит к тому, что никаких абсолютных общих свойств волн выделить не удаётся. Одним из часто встречающихся признаков волн считается близкодействие, проявляющееся во взаимосвязи возмущений в соседних точках среды или поля, однако в общем случае может отсутствовать и оно.

Среди всего многообразия волн выделяют некоторые их простейшие типы, которые возникают во многих физических ситуациях из-за математического сходства описывающих их физических законов. Об этих законах говорят в таком случае как о волновых уравнениях. Для непрерывных систем это обычно дифференциальные уравнения в частных производных в фазовом пространстве системы, для сред часто сводимые к уравнениям, связывающим возмущения в соседних точках через пространственные и временные производные этих возмущений[2]. Важным частным случаем волн являются линейные волны, для которых справедлив принцип суперпозиции.

По своему характеру волны подразделяются на:

По признаку распространения в пространстве: стоячие, бегущие.

По характеру волны: колебательные, уединённые (солитоны).

По типу волн: поперечные, продольные, смешанного типа.

По законам, описывающим волновой процесс: линейные, нелинейные.

По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях.

По геометрии: сферические (пространственные), одномерные (плоские), спиральные.

Отличие колебания от волны.

Бегущие волны, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»).

В основном физические волны не переносят материю, но возможен вариант, где происходит волновой перенос именно материи, а не только энергии. Такие волны способны распространяться сквозь абсолютную пустоту. Примером таких волн может служить нестационарное излучение газа в вакуум, волны вероятности электрона и других частиц, волны горения, волны химической реакции, волны плотности реагентов, волны плотности транспортных потоков.

Математическое описание:

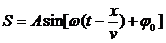
Волновое уравнение — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики