Энергетические зоны кристалла
 Чтобы понять возникновение зон в кристалле , рассмотрим n-ое количество одинаковых атомов. Каждый из этих атомов в отдельности имеет энергетический спектр. Если атомы одинаковые, то и энергетические спектры одинаковы. При сближении этих атомов одни и те же энергетические уровни в результате взаимодействия между атомами образуют совокупность, которую можно рассмотреть как расщепление одного энергетического уровня. В результате появятся энергетические зоны, которые могут частично перекрываться.
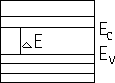
Чтобы понять возникновение зон в кристалле , рассмотрим n-ое количество одинаковых атомов. Каждый из этих атомов в отдельности имеет энергетический спектр. Если атомы одинаковые, то и энергетические спектры одинаковы. При сближении этих атомов одни и те же энергетические уровни в результате взаимодействия между атомами образуют совокупность, которую можно рассмотреть как расщепление одного энергетического уровня. В результате появятся энергетические зоны, которые могут частично перекрываться. 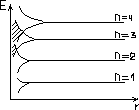 Если перекрытие зон не наблюдается, т.е. энергетические зоны разделены запрещенным промежутком, мы имеем дело с проводниками или диэлектриками. В случае перекрытия – с п/проводниками.Есть зоны полностью заполненные электронами при 0 К и полностью свободные при 0 К.Наивысшую заполненную электронами зону при 0 К назыв. валентной зоной проводимости.Для проводников валентная зона и зона проводимости перекрываются, образуя одну зону с близко расположенными уровнями, расстояние между которыми порядка 10-23 эВНаивысший заполненный электронами уровень при 0 К – уровень Ферми. Энергия , соответствующая этому уровню – энергия Ферми.У полупроводников и диэлектриков валентная зона и зона проводимости разделены запрещенным энергетическим интервалом – запрещенной зоной.Ec – дно зоны проводимости, Ev – потолок валентной зоны, ∆E – ширина запрещенной зоны.При 0 К все уровни валентной зоны заполнены в соответствии с принципом Паули.В зоне проводимости при 0 К электронов нет.Если заставить электрон из валентной зоны переместиться в зону проводимости (тепловое, фото-возбуждение, эл. полем), то в этой зоне электрон получит возможность свободного перемещения с одного энерг. ур-ня на другой.
Если перекрытие зон не наблюдается, т.е. энергетические зоны разделены запрещенным промежутком, мы имеем дело с проводниками или диэлектриками. В случае перекрытия – с п/проводниками.Есть зоны полностью заполненные электронами при 0 К и полностью свободные при 0 К.Наивысшую заполненную электронами зону при 0 К назыв. валентной зоной проводимости.Для проводников валентная зона и зона проводимости перекрываются, образуя одну зону с близко расположенными уровнями, расстояние между которыми порядка 10-23 эВНаивысший заполненный электронами уровень при 0 К – уровень Ферми. Энергия , соответствующая этому уровню – энергия Ферми.У полупроводников и диэлектриков валентная зона и зона проводимости разделены запрещенным энергетическим интервалом – запрещенной зоной.Ec – дно зоны проводимости, Ev – потолок валентной зоны, ∆E – ширина запрещенной зоны.При 0 К все уровни валентной зоны заполнены в соответствии с принципом Паули.В зоне проводимости при 0 К электронов нет.Если заставить электрон из валентной зоны переместиться в зону проводимости (тепловое, фото-возбуждение, эл. полем), то в этой зоне электрон получит возможность свободного перемещения с одного энерг. ур-ня на другой.
40 . Распределение Ферми-Дирака
Рассм совокупн. невзаимодейств элементов в одномерн. случ. наз-ся эл газом:
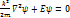 Мы рассмотрим случай когда эл-н находится в одномерн потенц. Яме решение уравнение Шрёденгера имеет вид
Мы рассмотрим случай когда эл-н находится в одномерн потенц. Яме решение уравнение Шрёденгера имеет вид 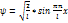 В соотв с принци паули на энергетич ур-не, заданном квант. числом n может находится 2 эл-на с противоположно направленными спинами. Если эл. газ Ферми содерж N электронов, то при нуле кельвинов электронами будут заполняться все уровни до уровня ферми. nэ=N/2
В соотв с принци паули на энергетич ур-не, заданном квант. числом n может находится 2 эл-на с противоположно направленными спинами. Если эл. газ Ферми содерж N электронов, то при нуле кельвинов электронами будут заполняться все уровни до уровня ферми. nэ=N/2
Сл-но энерг. Ферми в одномерном случ. будет равна: 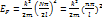
Распред. Ферми-Дирака можно получ. рассм. неупруг. соударение с атомами примеси.при небольш концентр примеси распред-е примеси подчин-ся статике. Больцмана. 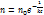 Предполож., что атом примеси может находится только в 2 сост. с энерг 0 и с энерг εРассм переход эл-на в руки соударения с атомом примеси с энерг Е и волн числом k в сотояниеE+εОпр вероятн. перехода эл-на из сост k в сост k’. Pkk’-? Переход будет происх. только в том случ., если сост с энерг E занято эл-ном. Вероятн., того что эл-н наход-ся в сост с энерг E=f(E)Сост. с энерг E+ε должно быть свободно . Вероятн., что это сост. свободно 1-f(E+ε).Для того чтобы такой переход был возможен , атом примеси должен наход-ся в сост с энерг ε Вероятн этого обозн через P(ε)Вероятн. одновр. наблюд независ. соб. опр-ся произв. вер. этих событий
Предполож., что атом примеси может находится только в 2 сост. с энерг 0 и с энерг εРассм переход эл-на в руки соударения с атомом примеси с энерг Е и волн числом k в сотояниеE+εОпр вероятн. перехода эл-на из сост k в сост k’. Pkk’-? Переход будет происх. только в том случ., если сост с энерг E занято эл-ном. Вероятн., того что эл-н наход-ся в сост с энерг E=f(E)Сост. с энерг E+ε должно быть свободно . Вероятн., что это сост. свободно 1-f(E+ε).Для того чтобы такой переход был возможен , атом примеси должен наход-ся в сост с энерг ε Вероятн этого обозн через P(ε)Вероятн. одновр. наблюд независ. соб. опр-ся произв. вер. этих событий 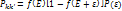 Вероятн обратн перехода будет отлична от 0, если сост. с энерг Е свободна,вероятноть этого равна.1-f(Е)Сост с энергией Е+ε будет f(E+ε). Атом примеси должен наход-ся в сост. с энерг 0 т.о
Вероятн обратн перехода будет отлична от 0, если сост. с энерг Е свободна,вероятноть этого равна.1-f(Е)Сост с энергией Е+ε будет f(E+ε). Атом примеси должен наход-ся в сост. с энерг 0 т.о 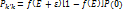 Согласно принцмпу детального равновесия вероятн этих переходов равны. т.е
Согласно принцмпу детального равновесия вероятн этих переходов равны. т.е 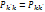
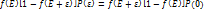
Атомы примеси подчиняются статистике Больцмана  Данное соотношение должно быть справедливо при любом знач температуры. Это возм. Если положить что
Данное соотношение должно быть справедливо при любом знач температуры. Это возм. Если положить что 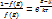 Решение системы приводит к результату f(E)=
Решение системы приводит к результату f(E)= 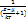 µ - химич концентрация при T=0K. Химич. Потенц. равен энергии Ферми.По своему смыслу функция распред. –это не что иное как средн число эл-нов , наход-ся в сост. с энерг. Е
µ - химич концентрация при T=0K. Химич. Потенц. равен энергии Ферми.По своему смыслу функция распред. –это не что иное как средн число эл-нов , наход-ся в сост. с энерг. Е 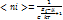 В случ высок. энергий когда E-
В случ высок. энергий когда E-  >>kT , то
>>kT , то 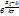 >>1
>>1
СВЕРХПРОВОДИМОСТЬ
Сверхпроводимость ¾ эффект скачкообразного падения сопротивления до нуля при T=Tk (критическая температура).
Сверхпроводимость открыта Киммерлинг-Оннесом в 1911 году, который наблюдал, что при Tk=4,2K электрическое сопротивление ртути скачкообразно падало до нуля.Сейчас известно ~ 1200 сверхпроводников.
МаксимальнуюTk=22,3K имеет сплав Na3Ge (1973 год).
Квантовая теория сверхпроводников создана в 1957 году Бардиным, Купером, Шриффером.
Резкий переход в сверхпроводящее состояние указывает на то, что все электроны проводимости одновременно во всём объёме металла переходят в новое состояние => должна быть корреляция состояний отдельных электронов. Физической причиной такой корреляции может быть взаимодействие электронов, но кулоновские силы приводят к отталкиванию. В данном же случае имеет место притяжение. Качественно механизм сверхпроводимости описывается через электронно-фононное взаимодействие. Это означает следующее: электроны, перемещаясь в решётке, деформируют её своим полем, т.е. смещают ионы из положения равновесия. Обратный переход ионов в исходное состояние сопровождается излучением энергии ¾ рождением фонона. Этот фонон поглощается другими электронами. В результате обмена фононами возникает связанное состояние электронов ¾куперовская пара. Минимальной энергией такая пара обладает, если импульсы взаимодействующих электронов равны по модули и противоположны по направлению, а спины ¾ антипараллельны.
Пара имеет спин = 0, т.е. она представляет собой бозе-частицу, которая не подчиняется принципу Паули. Они накапливаются в состоянии с минимальным значением энергии ¾бозе-конденсация.Куперовские пары, придя в согласованное движение, могут находиться в нём бесконечно долго сверхпроводимость.Участвовать в образовании куперовских пар могут лишь электроны, которые занимают энергетические уровни в слое;
При этом, если суммарная энергия двух электронов, находящихся на уровне Ферми, в нормальном состоянии = 2EF, то в состоянии сверхпроводимости энергия куперовской пары меньше и равна:
Куперовские пары при T=0 располагаются на уровне ниже уровня Ферми, который отделён от ближайшего уровня, отвечающего нормальному состоянию, наD.
При T=TkD=0 => сверхпроводимость исчезает.
