Магнитное поле, вектор магнитной индукции. Принцип суперпозиции.
МАГНИТНОЕ ПОЛЕ
- это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.
СВОЙСТВА ( стационарного) МАГНИТНОГО ПОЛЯ
Постоянное (или стационарное)магнитное поле - это магнитное поле, неизменяющееся во времени .
1. Магнитное полесоздается движущимися заряженными частицами и телами, проводниками с током, постоянными магнитами.
2. Магнитное поледействуетна движущиеся заряженные частицы и тела, на проводники с током, на постоянные магниты, на рамку с током.
3. Магнитное полевихревое, т.е. не имеет источника.
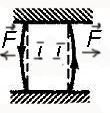
МАГНИТНЫЕ СИЛЫ
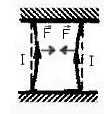
- это силы, с которыми проводники с током действуют друг на друга.
 ..................
.................. 
МАГНИТНАЯ ИНДУКЦИЯ
- это силовая характеристика магнитного поля.
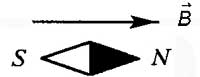
Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле.
Единица измерения магнитной индукции в системе СИ:
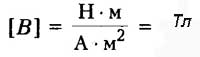
ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ
- это линии, касательными к которой в любой её точке является вектор магнитной индукции.

Однородное магнитное поле - это магнитное поле, у которого в любой его точке вектор магнитной индукции неизменен по величине и направлению; наблюдается между пластинами плоского конденсатора, внутри соленоида (если его диаметр много меньше его длины) или внутри полосового магнита.
Принцип суперпозиции магнитных полей: если магнитное поле создано несколькими проводниками с токами, то вектор магнитной индукции в какой-либо точке этого поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности:
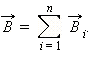 |
36 закон био-савара-лапласа. Поле прямого и кругового токов.Закон Био Савара Лапласа определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. Поле при этом создано постоянным током на некотором участке.
Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид.
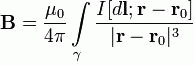
Исследования показали, что линии магнитной индукции поля кругового тока не являются правильными окружностями (рис. 2), но они замыкаются, обходя проводник, по которому идет ток. Направление линий магнитной индукции можно определить с помощью правила правого винта (правило буравчика): если головку винта вращать в направлении тока в проводнике, то поступательное движение острия винта покажет направление магнитной индукции в центре кругового тока.
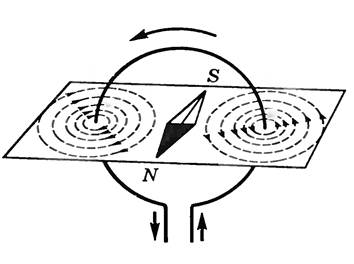
Рис. 2
В центре кругового тока модуль магнитной индукции может быть вычислен по формуле
B=μμ0I2R,
где R — радиус кругового проводника.
Магнитное поле кругового тока — неоднородное поле.
37 магнетики.МАГНЕТИК, вещество, обладающее магнитными свойствами, которые определяются наличием собственных или индуцированных внешним магнитным полем магнитных моментов, а также характером взаимодействия между ними. Различают диамагнетики, в которых внешнеемагнитное поле создает результирующий магнитный момент, направленный противоположно внешнему полю, и парамагнетики, в которых эти направления совпадают. Ряд веществ обладает так называемыми сильно магнитными свойствами, т.е. магнитные моменты в них расположены упорядоченно даже в отсутствие внешнего магнитного поля ниже некоторой критической температуры; к ним относятся ферро- и ферримагнетики (ниже Кюри точки), антиферромагнетики (антипараллельное расположение ниже Нееля точки), а также магнетики с более сложными (неколлинеарными) расположениями магнитных моментов (например, слабые ферромагнетики). Наибольшее применение в электро- и радиотехнике находят ферромагнитные металлы Fe, Ni, Co.
38 закон полного тока для магнитного поля в веществе.Таким образом, закон полного тока для магнитного поля в веществе утверждает, что циркуляция вектора напряженности магнитного поля 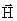 вдоль произвольного замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность, натянутую на этот контур:
вдоль произвольного замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность, натянутую на этот контур:
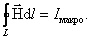 , , | (6.3.6) |
Выражение (6.3.6) – это закон полного тока в интегральной форме. В дифференциальной форме его можно записать:
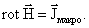 , , | (6.3.7) |
39 напряженность магнитного поля. Напряженностью магнитного поля называют векторную величину 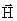 , характеризующую магнитное поле и определяемую следующим образом:
, характеризующую магнитное поле и определяемую следующим образом:
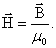 , , | (1.4.1) |
Напряженность магнитного поля заряда q, движущегося в вакууме равна:
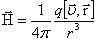 , , | (1.4.2) |
Это выражение показывает закон Био–Савара–Лапласа для 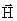 .
.
Напряженность магнитного поля 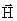 является, как бы, аналогом вектора электрического смещения
является, как бы, аналогом вектора электрического смещения 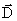 в электростатике.
в электростатике.
40. магнитный момент. Вращающий момент, действующий на магнитный момент в магнитном поле.действие магнитного поля на плоский контур с током определяется магнитным моментом контура pm, равным произведению силы тока I в контуре на площадь контура S:pm=IS (см. формулу (118.1)).
Единицей магнитного момента является ампер-метр в квадрате (А•м2). Чтобы дать представление об этой единице, укажем, что при силе тока 1 А магнитным моментом, равным 1 А•м2, обладает круговой контур радиуса 0,564 м (p•0,5642=1) либо квадратный контур со стороной квадрата, равной 1 м. При силе тока 10 А магнитным моментом 1 А•м2 обладает круговой контур радиуса 0,178 м (p•0,1782=0,1) и т. д.
Электрон, движущийся с большой скоростью по круговой орбите, эквивалентен круговому току, сила которого равна произведению заряда электрона е на частоту n вращения электрона по орбите: I=en. Если радиус орбиты равен r, а скорость электрона — v, то n=vl2pr и, следовательно, I=ev/2pr. Магнитный момент, соответствующий этому току,
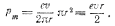
Магнитный момент является векторной величиной, направленной по нормали к контуру. Из двух возможных направлений нормали выбирается то, которое связано с направлением тока в контуре правилом правого винта [{рис. 211). Вращение винта с правой нарезкой в направлении, совпадающем с направлением тока в контуре, вызывает продольное перемещение винта в направлении n. Выбранная таким образом нормаль называется положительной. Направление вектора pm принимается совпадающим с направлением положительной нормали n. Если в однородном магнитном поле помещен плоский контур прямоугольной формы с током, то на него действует пара сил, стремящихся повернуть контур вокруг оси (рисунок в начале статьи).
Вращающий момент этой пары сил равен произведению величины одной из сил на расстояние (плечо) между токами приложения этих сил:
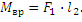
Вращающий момент, действующий на контур с током, можно определить по формуле
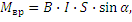
где В – магнитная индукция внешнего поля в теслах;
I – ток контура в амперах;
S – площадь проекции рамки на плоскость, перпендикулярную магнитным силовым линиям в квадратных метрах;
Мвр – вращающий момент в ньютон-метрах;
α – угол между перпендикуляром к плоскости контура и направлением магнитных силовых линий.
Контур с током стремитсяустановиться во внешнем магнитном поле так, чтобы внутри контура внешнее магнитное поле и собственное магнитное поле контура совпали по своему направлению. При этом, α = 0 иМвр = BIsin0 = 0.
Вращающий момент плоской катушки с числом витков ω определяется по формуле
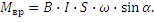
Направление пары сил, действующих на контур с током и на плоскую катушку, определяется по правилу левой руки.
Два достаточно длинных прямолинейных и параллельно расположенных проводника одинаковой длины с токами I1 и I2 взаимодействуют друг с другом, причем сила взаимодействия равна
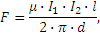
Сила лоренца и сила ампера.
| Действие магнитного поля на проводник с током Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. | |
| Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: F=B.I.ℓ. sin a — закон Ампера. | 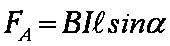 |
| Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током. | 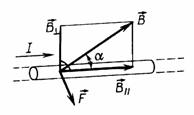 |
| Действие магнитного поля на движущийся заряд. | |
Сила, действующая на заряженную движущуюся частицу в магнитном поле, называетсясилой Лоренца: 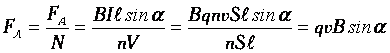 | 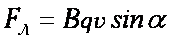 |
| Направление силы Лоренца (правило левой руки)Направление F определяется по правилу левой руки: вектор Fперпендикулярен векторам В и v.. | 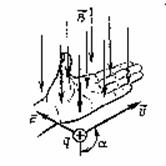 |
| Правило левой руки сформулировано для положительной частицы. Сила, действующая на отрицательный заряд будет направлена в противоположную сторону по сравнению сположительным. | 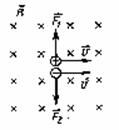 |
Если вектор v частицы перпендикулярен вектору В, то частица описывает траекторию в виде окружности: 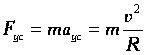 Роль центростремительной силы играет сила Лоренца: Роль центростремительной силы играет сила Лоренца: 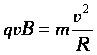 | 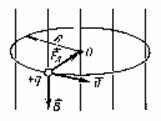 |
При этом радиус окружности: 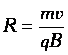 , а период обращения , а период обращения 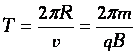 не зависит от радиуса окружности! не зависит от радиуса окружности! | 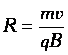 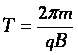 |
| Если вектор скорости и частицы не перпендикулярен В, то частица описывает траекторию в виде винтовой линии (спирали). | 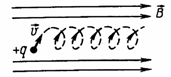 |
| Действие магнитного поля на рамку с током | |
| На рамку действует пара сил, в результате чего она поворачивается. 1. Направление вектора силы – правилу левой руки. 2. F=BIlsina=ma 3. M=Fd=BIS sina- вращающий момент | 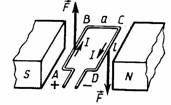 |
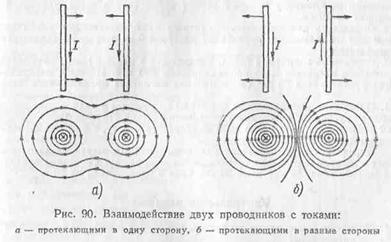
42 взаимодействие токов.Если близко один к другому расположены проводники с токами одного направления, то магнитные линии этих проводников, охватывающие оба проводника, обладая свойством продольного натяжения и стремясь сократиться, будут заставлять проводники притягиваться (рис. 90, а).
Магнитные линии двух проводников с токами разных направлений в пространстве между проводниками направлены в одну сторону. Магнитные линии, имеющие одинаковое направление, будут взаимно отталкиваться. Поэтому проводники с токами противоположного направления отталкиваются один от другого (рис. 90, б).
Рассмотрим взаимодействие двух параллельных проводников с токами, расположенными на расстоянии а один от другого. Пусть длина проводников равна l.
Магнитная индукция, созданная током I1 на линии расположения второго проводника, равна
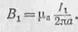
На второй проводник будет действовать электромагнитная сила
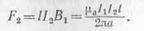
Магнитная индукция, созданная током I2 на линии расположения первого проводника, будет равна
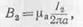
и на первый проводник действует электромагнитная сила
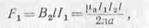
равная по величине силе F2
43 работа силы ампераДля вычисления этой работы рассмотрим проводник длиной l с током I (он может свободно двигаться), который помещен в однородное внешнее магнитное поле, которое перпендикулярно плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера, рассчитывается по формуле
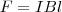
Под действием данной силы проводник передвинется параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, которая совершается магнитным полем, равна
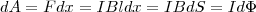
так как ldx=dS — площадь, которую пересекает проводник при его перемещении в магнитном поле, BdS=dФ — поток вектора магнитной индукции, который пронизывает эту площадь. Значит,
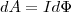 (1)
(1)
т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Данная формула справедлива и для произвольного направления вектора В.
Рассчитаем работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Будем считать, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения перейдет в положение М', изображенное на рис. 2 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж или от нас) дано на рисунке. Контур М условно разобьем на два соединенных своими концами проводника: AВС и CDА.
Работа dA, которая совершается силами Ампера при иссследуемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников AВС (dA1) и CDA (dA2), т. е.
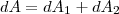 (2)
(2)
Силы, которые приложенны к участку CDA контура, образуют острые углы с направлением перемещения, поэтому совершаемая ими работа dA2>0. .Используя (1), находим, эта работа равна произведению силы тока I в нашем контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ2, который пронизывает контур в его конечном положении. Значит,
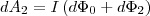 (3)
(3)
Силы, которые действуют на участок AВС контура, образуют тупые углы с направлением перемещения, значит совершаемая ими работа dA1<0. Проводник AВС пересекает при своем движении поток dФ0 сквозь поверхность, выполненную в цвете, и поток dФ1, который пронизывает контур в начальном положении. Значит,
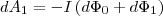 (4)
(4)
Подставляя (3) и (4) в (2), найдем выражение для элементарной работы:
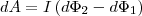
где dФ2—dФ1=dФ' — изменение магнитного потока сквозь площадь, которая ограничена контуром с током. Таким образом,
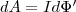 (5)
(5)
Проинтегрировав выражение (5), найдем работу, которая совершается силами Ампера, при конечном произвольном перемещении контура в магнитном поле:
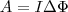 (6)
(6)
Магнитный поток. Основные теоремы магнитостатики. Магнитное поле соленоида. В однородном магнитном поле, модуль вектора индукции которого равен В, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол a с направлением вектора магнитной индукции В.
Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:
Φ = B · S · cos α
Единица измерения магнитного потока в систем СИ - 1 Вебер (1 Вб).
1 Вб = 1 Тл · 1 м2
Магнитный поток через контур максимален,если плоскость контура перпендикулярна магнитному полю. Значит угол a равен 00 .
Тогда магнитный поток рассчитывается по формуле:
Φmax = B · S
