Импульс фотона. Эффект Комптона

Импульс фотона: 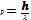.Где h(постоянная Планка)=6.63*10^-34, 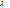-длина волны.

ЭффектКомптона-рассеяние электромагнитного излучения на свободном электроне, сопровождающееся уменьшением частоты излучения (открыт А. Комптоном в 1923 г.). В этом процессе электромагнитное излучение ведёт себя как поток отдельных частиц – корпускул (которыми в данном случае являются кванты электромагнитного поля - фотоны), что доказывает двойственную – корпускулярно-волновую – природу электромагнитного излучения. С точки зрения классической электродинамики рассеяние излучения с изменением частоты невозможно.
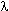Комптоновское рассеяние-это рассеяние на свободном электроне отдельного фотона с энергией Е = h = hc/ (h – постоянная Планка, – частота электромагнитной волны, 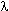– её длина, с – скорость света) и импульсом р = Е/с. Рассеиваясь на покоящемся электроне, фотон передаёт ему часть своей энергии и импульса и меняет направление своего движения. Электрон в результате рассеяния начинает двигаться. Фотон после рассеяния будет иметь энергию Е' = h ' (и частоту) меньшую, чем его энергия (и частота) до рассеяния. Соответственно после рассеяния длина волны фотона 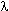' увеличится. Из законов сохранения энергии и импульса следует, что длина волны фотона после рассеяния увеличится на величину

,

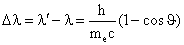где 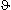- угол рассеяния фотона, а m_e- масса электрона.
58.Волновая функция. Гипотеза де Бройля

Волновая функция-комплексная функция, используемая в квантовой механике для вероятностного описания состояния квантовомеханическойсистемы;вероятность нахождения частицы в данном состоянии равна квадрату абсолютного значения амплитуды вероятности этого состояния.
Волновая функция зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат её модуля представлял вероятность обнаружить систему в положении, описываемом координатами.

Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор определяет представление волновой функции.
Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.
Для волновых функций справедлив принцип суперпозиции.

Гипотеза де Бройля:каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы остаются такими же, как и в случае электромагнитного излучения. Энергия 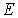и импульс 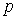фотона связаны с круговой частотой 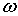и длиной волны 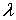соотношениями