Законы излучения абсолютно чёрного тела.

1) Закон Стефана-Больцмана Rт=δT⁴; Интегральная плотность излучения АЧ тела пропорцианальна 4-ой степени абсолютной температуры. δ=5,67*10^-8 Вт/м²K(с.4) – постоянная стефана-больцмана.

2) 1-й закон Вина (закон смещения Вина): λmax=b/T.Длинна волны, на которую приходится максимум спектральной плотности излучения АЧТ, обратно пропорциональна его абсолютной температуре. b=2,898*10^-3м*К.

Гипотеза Луи-де-Бройля. Волновая функция и её статический смысл.

Элект­роны в атомах движутся по законам, отличным от законов класси­ческой механики и электродинамики, Де Бройль предположил, что между корпускулярными и вол­новыми характеристиками электрона существует точно такая же связь, как между соответствующими характеристиками фотона. связь импульса фотона с длиной волны излучения: p=m_фc= m_фc²/c=hv/c=h/λили λ= h/p (45.2)

Де Бройль постулировал, что соотношение (45.2) справедливо не только для фотонов, но и для электронов. Впоследствии ока­залось, что это соотношение верно для любых микрочастиц и си­стем, состоящих из них. Электрон движется со скоростью v <c и его импульсp=m_ev где m_e=m_0e/(1-v²/c²)^1/2 (45.3)Таким образом, соотношение де Бройля сопоставляет электрону с импульсом р длину волны или λ= h/p= или λ= h/m_ev (45.4) При ускорении электрона в электрическом поле с разностью Потенциалов U, не превышающей 10⁴ в, масса электрона практически не отличается от массы покоя т_0е. Кинетическая энергия, приобретаемая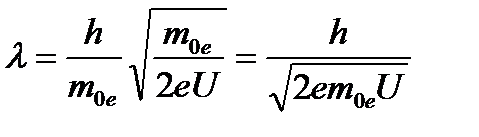

электроном в ускоряющем поле, равна

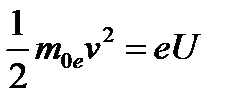
и скорость

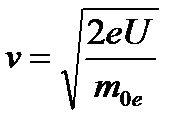
При размерах электронных приборов /«10 смλ>>lи волновые свойства для электронного пучка практически не про­являются. Волновые свойства, в частности дифракция электро­нов, могут наблюдаться на дифракционной решетке с по­стоянной порядка ~ К. Так же как и для рентгеновских лучей, дифракцию электро­нов можно пытаться обнару­жить с помощью естествен­ной — кристаллической ре­шетки Волновая функция (или вектор состояния) – комплексная функция, описывающая состояние квантовомеханической системы. Её знание позволяет получить максимально полные сведения о системе, принципиально достижимые в микромире. Так с её помощью можно рассчитать все измеряемые физические характеристики системы, вероятность пребывания её в определенном месте пространства и эволюцию во времени. Волновая функция может быть найдена в результате решения волнового уравнения Шредингера. Волновая функция ψ(x, y, z, t) ≡ ψ(x,t) точечной бесструктурной частицы является комплексной функцией координат этой частицы и времени.

Шредингера(стационарная).

Статистическое толкование волн де Брой-ля и соотношение неопреде­ленностей Гейзенберга при­вели к выводу, что уравнением движения в квантовой механике, описывающим дви­жение микрочастиц в различных силовых полях, должно быть уравнение, из которо­го бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное урав­нение должно быть уравнением относи­тельно волновой функции 4^е (х, у, г, /), так как именно она, или, точнее, величина l^l², определяет вероятность пребывания частицы в момент времени t в объеме dV, т. е. в области с координатами х и х-\-Ах, уи y-\-dy, г и z + dz. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть во­лновым уравнением,подобно уравнению, описывающему электромагнитные волны. Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шредингера, как и все основные уравне­ния физики не выводится, а постулируется. Правиль­ность этого уравнения подтверждается со­гласием с опытом получаемых с его по­мощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид

Ψ=Ψ₀cos(ωt-kx) – формула бегущей волны

Ψ= Ψ₀cos1/h(Et-px) – волновая функция фотона

Уравнение Шредингера

v²Ψ+2m/h(E-П)Ψ=0 – для стационарных постоянных

v²=d²Ψ/dx²+ d²Ψ/dy²+ d²Ψ/dz²