Классическая электронная теория проводимости металлов.

Исходя из представлений о свободных электронах, Друде разработал классическую теорию электропроводности металлов, которая затем была усовершенствована Лоренцем. Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершено свободно, пробегая в среднем некоторый путь . Правда в отличие от молекул газа , пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. Величину этой скорости легко оценить, исходя из формулы, связывающей плотность тока j с числом n носителей в единице объема, их зарядом е и средней скоростью 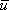: 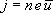. даже при больших плотностях тока средняя скорость упорядоченного движения зарядов в 10+Е8 раз меньше средней скорости теплового движения .

11.Теорема о циркуляции электростатического поля. Потенциальный характер эл-стат.поля.

Циркуляция вектора напряженности электрического поля вдоль любого замкнутого контура равна нулю.Теорема о циркуляции: Если циркуляция вектора Е по произвольному замкнутому полю = 0, то такое поле может быть создано неподвижными зарядами.

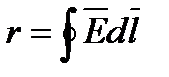
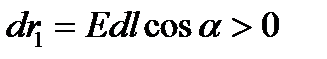
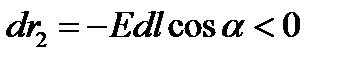
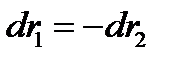
Потенциальный характер электростатического поля. Взаимодействие между неподвижными зарядами осуществляется посредством электростатического поля: взаимодействуют не заряды, а один заряд в месте своего расположения взаимодействует с полем, созданным другим зарядом. В этом заключается идея близкодействия - идея передачи взаимодействий через материальную среду, через поле.

12. Потенциал электростатического поля и его связь с напряжённостью.

Потенциалом электростатического поля в данной точке называют скалярную физическую величину, характеризующую энергетическое состояние поля в данной точке пространства и численно равную отношению потенциальной энергии, которой обладает пробный положительный заряд , помещенный в эту точку, к значению заряда. Потенциал – энергетическая силовая характеристика поля.На расстоянии r от точечного заряда q, создающего поле : .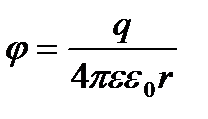

Потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности : 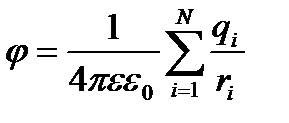. 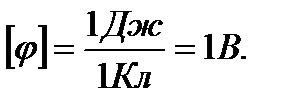Электрическое поле можно описать либо с помощью векторной величины Е, либо с помощью скалярной величины фи.

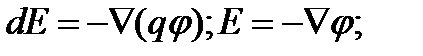
Эта формула позволяет по известным значениям фи найти напряженность поля в каждой точке. Можно решить и обратную задачу, т.е. по заданным значениям Е в каждой точке найти разность потенциалов между 2-мя произвольными точками поля.