Тонкие сферические линзы. Формула тонкой линзы, построение изображений в линзах.
Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями (одна из них обычно сферическая, иногда цилиндрическая, а вторая - сферическая или плоская), преломляющими световые лучи, способные формировать оптические изображения предметов.
Формула тонкой линзы :
(N-1)(1/R1+1/R2)=1/a+1/b.
N= n/n1- относительный показатель преломления (n и n1 - соответственно абсолютные показатели преломления линзы и окружающей среды)
R1, R2 - радиусы сфер, ограничивающих линзу.
a - расстояние от предмета до оптической плоскости линзы.
b - расстояние от изображения до оптической плоскости линзы.
Если а=¥, т.е. лучи падают на линзу параллельным пучком, то 1/b=(N-1)(1/R1+1/R2).
Соответствующее этому случаю расстояние b=OF=f называется фокусным расстоянием линзы, определяемым по формуле f=1/((N-1)(1/R1+1/R2)).
Если b=¥, т.е. изображение находится в бесконечности и, следовательно, лучи выходят из линзы параллельным пучком, то а=OF=f. Таким образом, фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Точки F, лежащие по обе стороны линзы на расстоянии, равном фокусному, называются фокусами линзы. Фокус - это точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оси.
Величина (N-1)(1/R1+1/R2)=1/f=Ф называется оптической силой линзы. Ее единица - диоптрия (дптр). Диоптрия - оптическая сила линзы с фокусным расстоянием 1м: 1дптр=1/м.
Поэтому можно записать : 1/a+1/b=1/f.
Построение изображения предмета в линзах осуществляется с помощью следующих лучей: 1) луча, проходящего через оптический центр линзы и не изменяющего своего направления; 2) луча, идущего параллельно главной оптической оси; после преломления в линзе этот луч (или его продолжение) проходит через второй фокус линзы; 3) луча (или его продолжения), проходящего через первый фокус линзы; после преломления в ней он выходит из линзы параллельно ее главной оптической оси. Отношение линейных размеров изображения и предмета называется линейным увеличением линзы. Отрицательным значениям линейного увеличения соответствует действительное изображение (оно перевернутое), положительным - мнимое изображение (оно прямое).
Пример построения изображения:
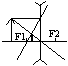 Изображение отсутствует мнимое, увеличенное
Изображение отсутствует мнимое, увеличенное
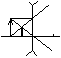
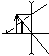
мнимое, уменьшенное, прямое
Основные характеристики: прямая, проходящая через центры кривизны поверхностей линзы, называется главной оптической осью. Для всякой линзы существует точка называемая оптическим центром линзы, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь. Оптический центр О линзы для простоты будем считать совпадающим с геометрическим центром средней части линзы (это справедливо только для двояковыпуклой и двояковогнутой линзы с одинаковыми радиусами кривизны обеих поверхностей; для плосковыпуклых и плосковогнутых линз оптический центр О лежит на пересечении главной оптической оси со сферической поверхностью); главная оптическая плоскость - плоскость, походящая через оптический центр линзы перпендикулярно главной оптической оси.
Дисперсия световых волн
Дисперсия света (ДС) – явление обусловленное зависимостью показателя преломления от длины волны. Для простоты в дальнешем рассмотрим преломление света на границе вакуум-данная среда, т.е. будем рассматривать зависимость абсолютного показателя преломления от длины волны n=f(λ). Дисперсия вещества (ДВ) – физическая величина, показывающая как быстро показатель преломления изменится с изменением длины волны. Если для двух длин волн λ1 и λ2, показатель преломления n1 и n2, то средний дисперсией в этом интервале будет
ν(в)=(n2-n1)/(λ2-λ1)=∆n/∆λ; ∆λà0, ν=dn/dλ. Для большинства прозрачных сред n монотонно убывает с увеличением длины волны.
Из графиков следует, что n наиболее резко изменяется
в области коротких длин волн => DB резко изменяется
в области коротких длин волн. n=f(λ)=A+B/λ(c.2),
где A и B – const, характеризующие природу вещества,
ν= - 2B/λ(c.3).
