Основные Законы геометрической оптики.

Основные Законы геометрической оптики.

Закон прямолинейного распространения света - в однородной среде свет распространяется прямолинейно. Закон независимости световых пучков – пучки световых лучей, пересекаясь, не взаимодействуют друг с другом и распространяются после пересечения независимо друг от друга. Лучи – линии, вдоль которых распространяется энергия световых электромагнитных волн. Эти линии проводятся перпендикулярно волновому фронту. Световой луч можно представить как ось достаточно узкого, остающегося при этом конечной ширины светового пучка. Таким образом луч – это понятие чисто геометрическое и самостоятельного физического значения не имеет.

Законы отражения света:

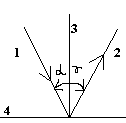1)луч падающий, луч отражённый и перпендикуляр, восстановленный на границе раздела двух сред в точке падения луча, лежат в одной плоскости. 2)угол падения = углу отражения (a=g).

Законы преломления света: 1) луч падающий, луч отражённый и перпендикуляр, восстановленный на границе раздела двух сред в точке падения луча, лежат в одно плоскости.2)отношение синуса угла падения a к синусу угла преломления b есть величина постоянная для данных сред: sina/sinb=n. N-величина, зависящая от свойств обеих граничащих сред, называемая относительным показателем преломления второй среды относительно первой. Если свет преломляется на границе “вакуум - прозрачная среда”, то соответствующий показатель преломления называется абсолютным показателем преломления прозрачной среды. Среда с большим значением абсолютного показателя преломления называется оптически более плотной. sina/sinb=n2/n1. n1sina=n2sinb.

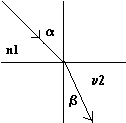
рассмотрим случай, когда лучи из оптически более плотной среды падают на границу раздела с оптически менее плотной средой.

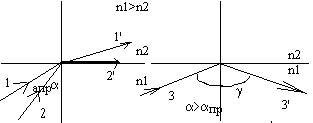
В этом случае угол преломления b, будет всё время больше угла падения a. Преломленный луч при увеличении угла падения a будет приближаться к границе раздела сред (луч 1’). При некотором угле падения, называемом предельным (a=aпр), преломленный луч (луч 2’) скользит почти вдоль поверхности раздела сред. Угол преломления bв этом случае = 90. при дальнейшем увеличении угла падения a (a>aпр), луч света полностью отражается от границы раздела сред (луч 3’). Это явление и называется полным отражением света.

n1sinaпр=n2sin90=n2; sinaпр=n2/n1; aпр=arcsin(n2/n1).

В случае, когда второй средой является воздух (n2=1): aпр=arcsin(1/n1)=arcsin(1/n).

Дисперсия световых волн

Дисперсия света (ДС) – явление обусловленное зависимостью показателя преломления от длины волны. Для простоты в дальнешем рассмотрим преломление света на границе вакуум-данная среда, т.е. будем рассматривать зависимость абсолютного показателя преломления от длины волны n=f(λ). Дисперсия вещества (ДВ) – физическая величина, показывающая как быстро показатель преломления изменится с изменением длины волны. Если для двух длин волн λ1 и λ2, показатель преломления n1 и n2, то средний дисперсией в этом интервале будет

ν(в)=(n2-n1)/(λ2-λ1)=∆n/∆λ; ∆λà0, ν=dn/dλ. Для большинства прозрачных сред n монотонно убывает с увеличением длины волны.

Из графиков следует, что n наиболее резко изменяется

в области коротких длин волн => DB резко изменяется

в области коротких длин волн. n=f(λ)=A+B/λ(c.2),

где A и B – const, характеризующие природу вещества,

ν= - 2B/λ(c.3).

Использование ИНТЕРФЕРЕНЦИИ

Интерференция применяется в сверхточных претензионных измерениях. Используются приборы – интерферометры, в их основе лежит явление интерференции. 2-ая область – контроль за чистотой обработки поверхности высокого класса точности. 3) для определения коэффициента линейности расширения твердого тела – делатометр. 4) просветление оптики.

ПОЛЯРИЗАЦИЯ СВЕТА

Законы Вина.

Немецкий физик Вин установил соотношение между 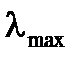, соответствующей максимальной излучательности 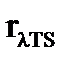абсолютно черного тела и его температурой:

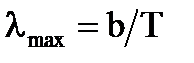(3)

где 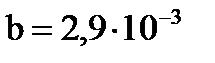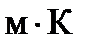. Выражение (3) отражает математически закон смещения Вина.

Из анализа кривых на рисунке 1 следует, что максимальная спектральная излучательность 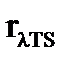пропорциональна пятой степени температуры:

,

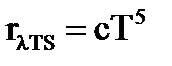(4)

где - спектральная константа равная .

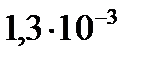
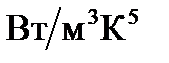Излучение АЧТ ГИПОТЕЗА ПЛАНКА. ОБЪЯСНЕНИЕ ЯВЛЕНИЯ ТЕПЛОВОГО ИЗЛУЧЕНИЯ

Эта зависимость была установлена эксперементально.

Пытались найти аналитический вид r (инд.λT) (в) как

функцию λ и T. r (индекс λT) = f (λ, T). Заслуживает

внимания соотношение, полученное Релоем и

Джинсом. Они попытались найти аналитический вид

этой функции на основе классической физики и

класической статике, в частности, используя теорему классической физики о равном распределении энергии по степеням свободы. Пусть имеется замкнутая полость с абсолютно отражающими стенками. Если эту полость нагреть, то стенки полости начнут излучать эл-маг волны. Частично излучение будет отражаться, частично поглощаться, так что в полости установится равновесие между излучением и поглощением, т.е. полость будет заполнена эл-маг волнами различной интенсивности, длины и поляризации хаотически распространяющихся по всей полости. Согласно теореме о равном распределении энергии по степеням свободы, энергия каждого электро-магнитного колебания: E=2*(1/2)*kT. Если размеры полости известны, то можно считать, по законам статической физики, число колебаний, а следовательно и излучательную способность (энергию, излучаемую в единицу площади). Эти расчеты привели Релея и Джинса к соотношению: r (индекс λТ) (в) = 2πckTλ(c. –4) – формула Релея-Джинса. Формула хорошо совпадает с экспериментальной зависимостью в области длинных длин волн и резко расходится вобласти коротких длин волн.

Rэ = ∫[0 - ∞] r (идекс λТ) dλ=2ckT ∫[0 - ∞] dλ/λ(c.4)=∞ - ультрафиолетовая катастрофа. С точки зрения классической физики вывод формулы Релея-Джинса является безупречным. Резкое расхождение с опытом означает, что при тепловом излучении проявляются такие закономерности, которые не нашли отражения в классической физике. В 1900 г. Планку удалось найти аналитический вид функции r (инд. λТ) (в), в точности соответствующий экспериментаьной кривой. Он исходит из положений, противоречащих классической физике. Согласно гипотезе Планка, изучение и поглощение энергии телами происходит не в виде непрерывного процесса, а дискретно, порциями, которые он назвал квантами эл-маг излучения. КВАНТЫ локализованы в очень маленьком объеме и распространяются в пространстве подобно частицам. Кроме того, кванты обладают и другими свойствами частиц. Основное свойство – сосредоточенная в них энергия. Энергия квантов определяется из свойства излучения. Согласно Планку, энергия квантов определяется частотой излучения и связана с частотой так – ε=hν; h=6,62*10(c.-34)Дж*с. Поскольку кванты обладают энергией, ε=mc(c.2)=hν; m (индекс p)=hν/с(с.2) (масса кванта или фотона),

Pф=m (инд. ф) * c = hν/c (импульс фотона). Гипотеза Планка противоречит ан. представлениям классической физики, согласно которым такие физические величины как энергия, импульс должны меняться непрерывно => и тепловое излучение должно представлять собой непрерывный поток, но из таких представлений вытекает формула Релея-Джинса, которая резко расходится с экспериментальной кривой в области больших длин волн, т.е. больших частот, где дискретностью принебрегать нельзя. В области больших частот всей энергии теплового возбуждения тела недостаточно, чтобы тело испустило хотя бы один квант такой энергии. Вот почему излучающая способность АЧТ падает до нуля. В этом и заключается объяснение явления теплового излучения и разрешения ультрафиолетовой катастрофы классической физики. На основании своих рассуждений и квантовой статистики квант получ. r (инд. λT) (в) = 2πhc(c.2) *

* (λ(c.-5) / e (c. hc/λkT) – 1) – ФОРМУЛА ПЛАНКА. Она совпадает с экспериментальной зависимостью от длины волны.

ЗАКОНА ФОТОЭФФЕКТА

1) количество фотоэлектронов, вырываемых в единицу времени с поверхности вещества, пропорционально интенсивности падающего светового потока. 2) максимальная скорость фотоэлектронов не зависит от интенсивности падающего светового потока. 3) скорость фотоэлектрона определяется частотой падающего светового потока. 4) для каждого вещества существует своя красная граница фотоэффекта, т.е. минимальная частота или максимальная длина волны, при которой фотоэффект еще возможен.

22. Квантовая теория фотоэффекта Уравнение Эйнштейна для фотоэффекта

Эффект Комптона.

Наиболее полно корпускулярные свойства проявляются в эффекте Комптона. В 1923 году американский физик Комптон исследовал рассеяние рентгеновских лучей на парафине, атомы которого легкие.

Рассеяние рентгеновских лучей с волновой точки зрения связано вынужденными колебаниями электронов вещества, так что частота рассеянного света должна совпадать с частотой падающего света. Однако в рассеянном свете обнаружилась большая длина волны 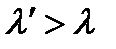. 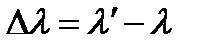не зависит от длины волны рассеиваемых рентгеновских лучей и от материала рассеивающего вещества, но зависит от направления рассеивания. 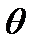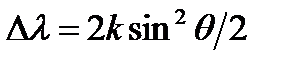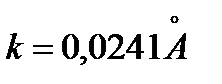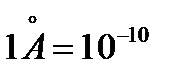Пусть - угол между направлением первичного пучка и направлением рассеянного света, тогда , где ( м).

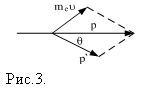
Этот закон верен для легких атомов (H₂, C₂, Br, Al) имеющих электроны, слабо связанные с ядром. Процесс рассеяния можно объяснить упругим столкновением фотонов с электронами. Под действием рентгеновских лучей электроны легко отделяются от атома. Поэтому можно рассматривать рассеяние свободными электронами. Фотон, имеющий импульс 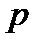, сталкивается с покоящимся электроном и отдает ему часть энергии, а сам приобретает импульс 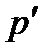(рис.3).

Используя законы сохранения энергии и импульса для абсолютно упругого удара, получим для 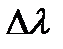выражение: 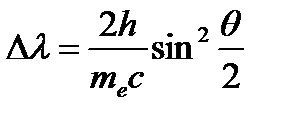, которое совпадает с экспериментальным, при этом 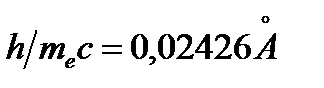, что и доказывает корпускулярную теорию света.

Уравнение Шредингера.

Квантовая механика способна объяснить поведение микрочастиц. Подобно тому, как законы Ньютона не выводятся, а является обобщением большого числа опытных фактов, так и уравнение Шредингера не выводятся. Оно постулируется. Шредингер записал уравнение, основываясь на экспериментальных результатах.

Состояние микрочастиц в квантовой механике описывается волновой функцией 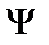. Она является функцией координат и времени и может быть найдена из уравнения Шредингера:

.

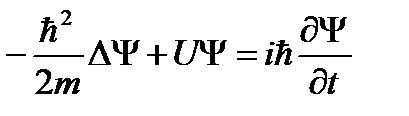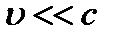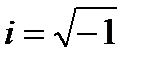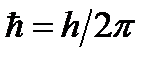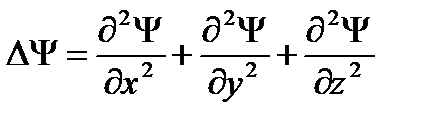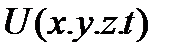Это временное уравнение Шредингера для случая, когда . Здесь i - мнимая единица ( ), , m - масса частицы, - оператор Лапласа ( ), - потенциальная энергия частицы.

Постулаты Бора.

Для того, чтобы объяснить линейчатые спектры атомов датский физик Нильс Бор в 1913 году вводит два постулата.

Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся во времени) состояния, в которых он не излучает энергию. Энергии этих состояний образуют дискретный ряд: 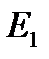, , 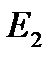…, 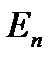. Стационарным состояниям атома соответствуют орбиты, по которым движутся электроны. Хотя электроны движутся по стационарным орбитам с ускорением, они не излучают и не поглощают энергию.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные значения момента импульса, удовлетворяющие условию:

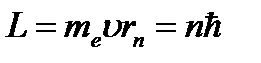, n=1, 2, 3,…, где 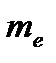- масса электрона, 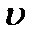- его скорость по n-ой орбите радиуса , .

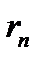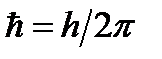Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) квант с энергией:

.

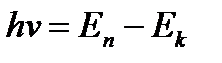При 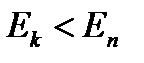происходит излучение фотона (переход из состояния с большей энергией в состояние с меньшей энергией), при 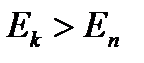- поглощение фотона (переход атома в состояние с большей энергией).

Набор возможных дискретных частот 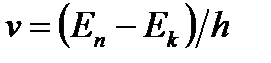определяет линейчатый спектр атома.

Основные Законы геометрической оптики.

Закон прямолинейного распространения света - в однородной среде свет распространяется прямолинейно. Закон независимости световых пучков – пучки световых лучей, пересекаясь, не взаимодействуют друг с другом и распространяются после пересечения независимо друг от друга. Лучи – линии, вдоль которых распространяется энергия световых электромагнитных волн. Эти линии проводятся перпендикулярно волновому фронту. Световой луч можно представить как ось достаточно узкого, остающегося при этом конечной ширины светового пучка. Таким образом луч – это понятие чисто геометрическое и самостоятельного физического значения не имеет.

Законы отражения света:

1)луч падающий, луч отражённый и перпендикуляр, восстановленный на границе раздела двух сред в точке падения луча, лежат в одной плоскости. 2)угол падения = углу отражения (a=g).

Законы преломления света: 1) луч падающий, луч отражённый и перпендикуляр, восстановленный на границе раздела двух сред в точке падения луча, лежат в одно плоскости.2)отношение синуса угла падения a к синусу угла преломления b есть величина постоянная для данных сред: sina/sinb=n. N-величина, зависящая от свойств обеих граничащих сред, называемая относительным показателем преломления второй среды относительно первой. Если свет преломляется на границе “вакуум - прозрачная среда”, то соответствующий показатель преломления называется абсолютным показателем преломления прозрачной среды. Среда с большим значением абсолютного показателя преломления называется оптически более плотной. sina/sinb=n2/n1. n1sina=n2sinb.

рассмотрим случай, когда лучи из оптически более плотной среды падают на границу раздела с оптически менее плотной средой.

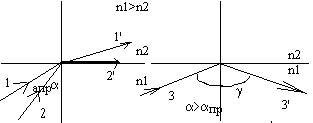
В этом случае угол преломления b, будет всё время больше угла падения a. Преломленный луч при увеличении угла падения a будет приближаться к границе раздела сред (луч 1’). При некотором угле падения, называемом предельным (a=aпр), преломленный луч (луч 2’) скользит почти вдоль поверхности раздела сред. Угол преломления bв этом случае = 90. при дальнейшем увеличении угла падения a (a>aпр), луч света полностью отражается от границы раздела сред (луч 3’). Это явление и называется полным отражением света.

n1sinaпр=n2sin90=n2; sinaпр=n2/n1; aпр=arcsin(n2/n1).

В случае, когда второй средой является воздух (n2=1): aпр=arcsin(1/n1)=arcsin(1/n).