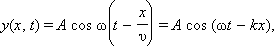Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
Если в одномерной модели твердого тела один или несколько шариков сместить в направлении, перпендикулярном цепочке, то возникнет деформация сдвига. Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия. При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна.
В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появляется. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах.
Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудойA колебания частиц, частотойf и длиной волныλ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.
Смещение y(x, t) частиц среды из положения равновесия в синусоидальной волне зависит от координаты x на оси OX, вдоль которой распространяется волна, и от времени tпо закону:
|
где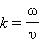 
– так называемоеволновое число, ω = 2πf – круговая частота.
На рис. 2.6.4 изображены «моментальные фотографии» поперечной волны в два момента времени: t и t + Δt. За время Δt волна переместилась вдоль оси OX на расстояние υΔt. Волны, все точки которых перемещаются с одной и той же скоростью, принято называть бегущими (в отличие от стоячих волн, см. далее).
 |
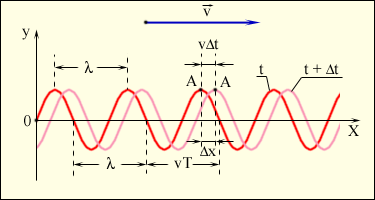| Рисунок 2.6.4. «Моментальные фотографии» бегущей синусоидальной волны в момент времени t и t + Δt. |
Длиной волны λ называют расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за период Т, следовательно, λ = υT, где υ – скорость распространения волны.
Для любой выбранной точки на графике волнового процесса (например, для точки A на рис. 2.6.4) выражение ωt – kx не изменяется по величине. С течением времени t изменяется и координата x этой точки. Через промежуток времени Δt точка A переместится по оси OX на некоторое расстояние Δx = υΔt. Следовательно:
| ωt – kx = ω(t + Δt) – k(x + Δx) = const или ωΔt = kΔx. |
Отсюда следует:
 |
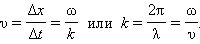Таким образом, бегущая синусоидальная волна обладает двойной периодичностью – во времени и пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны λ. Волновое число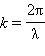 
является пространственным аналогом круговой частоты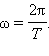 
Обратим внимание на то, что уравнение
|
описывает синусоидальную волну, распространяющуюся в направлении, противоположном направлению оси OX, со скоростью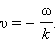 
В бегущей синусоидальной волне каждая частица среды совершает гармонические колебания с некоторой частотой ω. Поэтому, как и в случае простого колебательного процесса, средняя потенциальная энергия, запасенная в некотором объеме среды, равна средней кинетической энергии в том же объеме.