Свободные незатухающие электромагнитные колебания в колебательном контуре

Краткая теория

Свободные незатухающие электромагнитные колебания можно получить в электрической цепи, состоящей из последовательно соединенных конденсатора емкостью С, катушки индуктивностью L и резистора сопротивлением R:

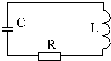
Такую электрическую цепь называют колебательным контуром, потому что в ней могут происходить периодические изменения электрического заряда и разности потенциалов на обкладках конденсатора, а также электрического тока в цепи. Периодические колебания перечисленных физических величин достаточно вызвать даже при кратковременном подключении конденсатора колебательного контура к источнику постоянного тока. Однако, из-за потерь электрической энергии, связанной с нагреванием катушки и резистора, имеющих электрическое сопротивление R, колебания в контуре будут затухающими.

Свободные незатухающие электромагнитные колебания можно получить только в идеализированном случае, когда можно пренебречь электрическим сопротивлением (R 0) контура. Такие свободные незатухающие колебания называют еще собственными электромагнитными колебаниями.

Можно доказать, что в колебательном контуре происходят гармонические колебания заряда, согласно закону:

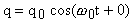, (1)

или

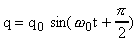, (2)

где : q - мгновенное значение заряда конденсатора;

q₀ - амплитудное значение электрического заряда;

₀ - собственная частота колебаний в контуре.

Форма записи (через cos или sin) не имеет значения, так как отличие будет определяться лишь начальными условиями, а именно различной начальной фазой колебаний. Зная связь между зарядом конденсатора и разностью потенциалов на его обкладках:

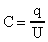, (3)

можно аналогично записать гармонические колебания разности потенциалов:

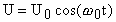, (4)

или

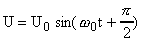, (5)

где: U - мгновенное значение напряжения на обкладках конденсатора;

U₀ - амплитудное значение напряжения;

₀ - собственная частота колебаний в контуре.

Сила тока является первой производной от электрического заряда по времени:

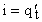. (6)

Поэтому гармонические колебания силы тока в колебательном контуре будут происходить по закону:

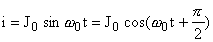, (7)

где: i - мгновенное значение тока в контуре;

J₀ = q₀ ₀ - амплитудное значение тока;

₀ - собственная частота колебаний в контуре.

Циклическая частота ₀ называется собственной частотой электромагнитных колебаний, она зависит только от параметров колебательного контура, а именно - от емкости конденсатора С и индуктивности L:

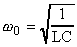. (8)

Период собственных электромагнитных колебаний, соответственно, вычисляется по формуле:

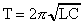. (9)

Эта формула была впервые получена английским ученым В.Томсоном и называется формулой Томсона.

Физические процессы, происходящие в колебательном контуре, сопровождается непрерывными преобразованиями одного вида энергии в другой, а именно: энергия электрического заряда конденсатора превращается в энергию магнитного поля катушки и наоборот. При этом, в полном соответствии с законом сохранения и превращения энергии, полная энергия в колебательном контуре остается величиной постоянной:

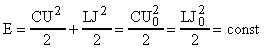, (10)

где: U и J - соответственно напряжение на обкладках конденсатора и сила тока в контуре в любой момент времени; U₀ и J₀ - амплитудные (максимальные) значения этих же величин.

Методические указания к решению задач

Задачи на свободные электромагнитные колебания можно условно разделить на две основные группы: задачи с использованием общих законов электромагнитных колебаний (1) - (7) и задачи, связывающие основные характеристики электромагнитных колебаний с параметрами колебательного контура (8), (9). В том и другом случае часто приходится учитывать энергетические преобразования в контуре (10).

Основная трудность при решении задач первой группы заключается в правильном составлении уравнений (1) - (7) по заданным характеристикам колеблющейся величины q₀, U₀, J₀. Важно знать следующее, что если задано значение колеблющейся величины в начальный момент времени t = 0, то форма записи закона гармонического колебания может быть выбрана произвольно (через синус или косинус), так как найденное значение начальной фазы ₀ будет соответствовать той или иной форме записи. А вот значение колеблющейся величины в произвольный момент времени будет зависеть от формы записи закона гармонических колебаний. Поэтому, если в условии указывается начальная фаза колебаний ₀, то должно быть указание на тригонометрическую функцию, через которую должен быть записан закон колебаний. Часто встречается и обратная задача - по заданному закону гармонических колебаний необходимо определить основные характеристики колебательного движения.

Задачи второй группы решаются на основании формул (8), (9).

Наиболее распространены задачи комбинированного типа, когда надо учитывать и закон гармонических колебаний и формулу Томсона.

Примеры решения задач

Задача № 1. Заряд q на пластинах конденсатора колебательного контура изменяется с течением времени t по закону 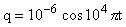. Записать закон зависимости силы тока от времени i(t). Найти период и частоту колебаний в контуре, амплитуду колебаний заряда и амплитуду колебаний силы тока i(t).

Дано:

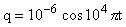
Найти:

T, , q_m, J_m -?

Решение:

Чтобы записать закон зависимости силы тока от времени, надо, прежде всего, воспользоваться соотношением (6). Получим:

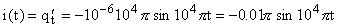
Сравнивая полученное выражение с формулой (7), нетрудно записать по аналогии, что:

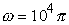
Далее, учитывая связь периода колебаний Т с круговой частотой  по формуле: 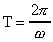, найдем значение периода колебаний Т:

; .

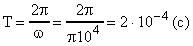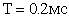Затем, воспользовавшись связью круговой частоты  с линейной , определим частоту:

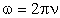или ; ; .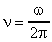

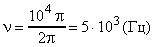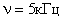Амплитудные значения колебаний силы тока J и заряда q найдем из сравнения заданной зависимости q(t) и полученной зависимости i(t) с формулами (1) и (7).

Получим: ; ; .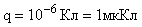

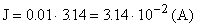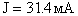Задача № 2. В колебательном контуре совершаются незатухающие электромагнитные колебания. Определить силу тока в контуре при t = 0,002 с от начала отсчета, если заряд конденсатора изменяется по гармоническому закону:

.

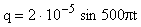Дано:

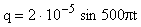
t = 0,002 с

Найти:

i - ?

Найдем уравнение гармонического колебания силы тока в колебательном контуре, а затем вычислим мгновенное значение силы тока i при t = 0,002 с:

;

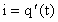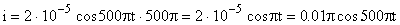
При t = 0,002 с получим:

; .

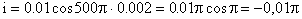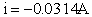Задача № 3. В колебательном контуре происходят незатухающие электромагнитные колебания. Определить максимальную силу тока в контуре, если емкость конденсатора С = 210^-5 Ф, индуктивность катушки L = 5 Гн и заряд конденсатора меняется по закону .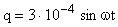

Дано:

С = 210^-5 Ф

L = 5 Гн

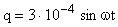
Найти:

J - ?

В данной задаче для определения амплитудного значения силы тока J₀ удобнее воспользоваться законом сохранения энергии (10), записав его в виде:

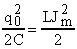
Энергию электрического поля выразили через электрический заряд, воспользовавшись соотношением:

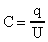Откуда: 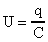и .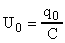

Получим следующее выражение:

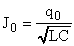
Максимальное значение заряда q₀ найдем из заданного уравнения q(t), сравнив его с формулой (1).

Получим: .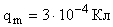

Окончательно вычисляем максимальное значение силы тока:

.

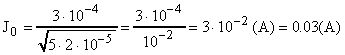Задача 4. Колебательный контур приемника состоит из слюдяного конденсатора, площадь пластин S которого 800 см², а расстояние d между ними 1 мм, и катушки. На какую длину волны резонирует этот контур, если максимальное значение напряжения на пластинах конденсатора в 100 раз больше максимального значения силы тока в катушке? Активным сопротивлением контура пренебречь.

Дано:

 = 7

S = 810^-6 м²

d = 110^-3 м

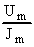= 100

₀ = 8.8510^-12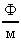

Найти:

 - ?

Длина волны  связана с периодом Т колебаний по формуле:

,

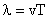где: v - скорость электромагнитных волн в данной среде;

В вакууме она равна - 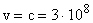м/с.

Период собственных колебаний определяется по формуле (9):

.

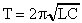Электроемкость конденсатора С можно вычислить, воспользовавшись данными задачи по формуле:

.

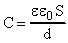Для нахождения индуктивности L катушки надо воспользоваться законом сохранения энергии в применении к заданному контуру:

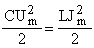; Откуда: .

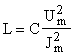Решая задачу в общем виде, окончательно получим:

; .

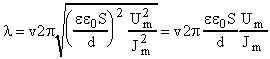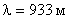Задача 5. Колебательный контур состоит из конденсатора емкости 2,510^-2 мкФ и катушки с индуктивностью 101,510^-2 Гн. Пластинам конденсатора сообщают заряд 2,5 мкКл. Найти значение силы тока i в контуре в тот момент, когда напряжение на пластинах конденсатора равно 70,7 В. Активным сопротивлением цепи пренебречь.

Дано:

С = 2,510^-8 Ф

L = 101,510^-2 Гн

q = 2,510^-6 Кл

U = 70,7 В

Найти:

i - ?

Для успешного решения задачи надо первоначально написать уравнения изменения напряжения на пластинах конденсатора U(t) и силы тока i(t).

Пусть начальный момент времени соответствует максимальному заряду q₀ на пластинах конденсатора и закон изменения заряда со временем будет: .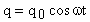

Тогда с учетом соотношения: 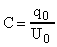можно утверждать что при t = 0 напряжение на пластинах также будет иметь максимальное значение. В этом случае уравнение U(t) записывается в виде: 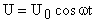, где: 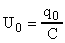; U_m = 100 В.

Для написания уравнения i(t) учтем, что .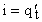

Отсюда получим: 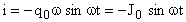, где: 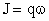- амплитудное значение тока.

Круговую частоту  можно вычислить через период колебаний Т по формуле: .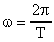

Учитывая формулу Томсона (9), окончательно получаем:

; .

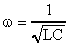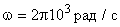Отсюда: максимальная сила тока будет равна:

.

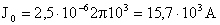Вычислим значения напряжения на пластинах конденсатора и силы тока:

; .

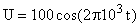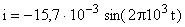Уравнение изменения напряжения на пластинах конденсатора позволит вычислить нужный момент времени:

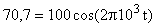или 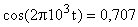. Откуда t = 12,510^-5 с.

Осталось вычислить силу тока i в момент времени t, воспользовавшись уравнением изменения силы тока:

.
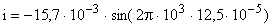
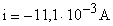