Уравнение состояния идеального газа - уравнение Менделеева-Клапейрона
Из основного уравнения молекулярно-кинетической теории (см. формулу (14)) следует закон Авогадро: в равных объемах разнородных газов при одинаковых условиях (одинаковой температуре и одинаковом давлении) содержится одинаковое число молекул:
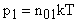 (для одного газа),
(для одного газа),
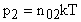 (для другого газа).
(для другого газа).
Если V1 = V2; Т1 = Т2; 1 = 2, то n01 = n02.
Напомним, что единицей количества вещества в системе СИ является моль (грамммолекула) масса одного моля вещества называется молярной массой этого вещества. Число молекул, содержащихся в одном моле разных веществ одинаково и называется число Авогадро (NA = 6,021023 1/моль).
Запишем уравнение состояния идеального газа для одного моля:
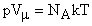 , где V - объем одного моля газа;
, где V - объем одного моля газа; 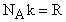 (универсальная газовая постоянная).
(универсальная газовая постоянная).
Окончательно имеем: 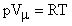 (26).
(26).
Уравнение (26) называется уравнением Клапейрона (для одного моля газа). При нормальных условиях (р = 1,013105 Па и Т = 273,150К) молярный объем любого газа Vm = 22,410-3 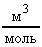 . Из формулы (26) определим
. Из формулы (26) определим 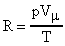 ;
; 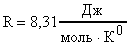 . От уравнения (26) для моля газа можно перейти к уравнению Менделеева-Клапейрона для любой массы газа m. Отношение
. От уравнения (26) для моля газа можно перейти к уравнению Менделеева-Клапейрона для любой массы газа m. Отношение  дает число молей газа. Левую и правую части неравенства (26) умножим на
дает число молей газа. Левую и правую части неравенства (26) умножим на  . Имеем
. Имеем 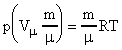 , где
, где 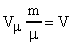 (объем газа). Окончательно запишем:
(объем газа). Окончательно запишем: 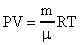 (27). Уравнение (27) - уравнение Менделеева-Клапейрона. В это уравнение можно внести плотность газа
(27). Уравнение (27) - уравнение Менделеева-Клапейрона. В это уравнение можно внести плотность газа 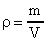 и
и 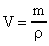 . В формуле (27) заменим V и получим
. В формуле (27) заменим V и получим 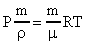 или
или 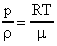 (28).
(28).
9.Опытные газовые законы. Давление смеси идеальных газов (закон Дальтона)
Опытным путем, задолго до появления молекулярно-кинетической теории, был открыт целый ряд законов, описывающих равновесные изопроцессы в идеальном газе. Изопроцесс - это равновесный процесс, при котором один из параметров состояния не изменяется (постоянен). Различают изотермический (T = const), изобарический (p = const), изохорический (V = const) изопроцессы.
Изотермический процесс описывается законом Бойля-Мариотта: "если в ходе процесса масса и температура идеального газа не изменяются, то произведение давления газа на его объем есть величина постоянная 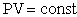 (29). Графическое изображение уравнения состояния называют диаграммой состояния. В случае изопроцессов диаграммы состояния изображаются двумерными (плоскими) кривыми и называются соответственно изотермами, изобарами и изохорами.
(29). Графическое изображение уравнения состояния называют диаграммой состояния. В случае изопроцессов диаграммы состояния изображаются двумерными (плоскими) кривыми и называются соответственно изотермами, изобарами и изохорами.
Изотермы, соответствующие двум разным температурам, приведены на рис. 6.
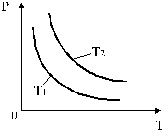
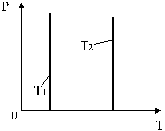
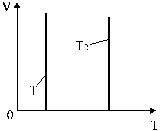
Рис. 6
Изобарический процесс описывается законом Гей-Люссака: "если в ходе процесса давление и масса идеального газа не изменяются, то отношение объема газа к его абсолютной температуре есть величина постоянная:
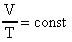 (30).
(30).
Изобары, соответствующие двум разным давлениям, приведены на рис.7.
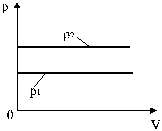
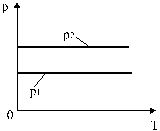
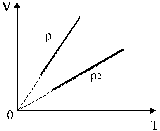
Рис. 7
Уравнение изобарического процесса можно записать иначе:
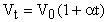 (31), где V0 - объем газа при 00С; Vt - объем газа при t0C; t - температура газа в градусах Цельсия; - коэффициент объемного расширения. Из формулы (31) следует, что
(31), где V0 - объем газа при 00С; Vt - объем газа при t0C; t - температура газа в градусах Цельсия; - коэффициент объемного расширения. Из формулы (31) следует, что 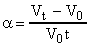 . Опыты французского физика Гей-Люссака (1802 г) показали, что коэффициенты объемного расширения всех видов газов одинаковы и
. Опыты французского физика Гей-Люссака (1802 г) показали, что коэффициенты объемного расширения всех видов газов одинаковы и 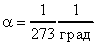 , т.е. при нагревании на 10С газ увеличивает свой объем на
, т.е. при нагревании на 10С газ увеличивает свой объем на 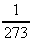 часть того объема, который он занимал при 00С. На рис. 8 изображен график зависимости объема газа Vt от температуры t0C.
часть того объема, который он занимал при 00С. На рис. 8 изображен график зависимости объема газа Vt от температуры t0C.
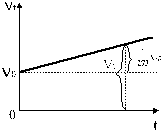
Рис. 8
Изохорический процесс описывается законом Шарля: "если в ходе процесса объем и масса идеального газа не изменяются, то отношение давления газа к его абсолютной температуре есть величина постоянная:
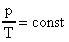 (32)
(32)
Изохоры, соответствующие двум разным объемам, приведены на рис. 9.
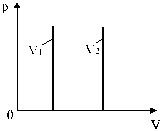
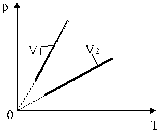
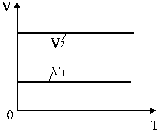
Рис. 9
Уравнение изохорического процесса можно записать иначе:
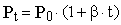 (33),
(33),
где 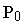 - давление газа при
- давление газа при 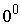 С;
С; 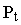 - давление газа при t; t - температура газа в градусах Цельсия;
- давление газа при t; t - температура газа в градусах Цельсия; 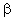 - температурный коэффициент давления. Из формулы (33) следует, что
- температурный коэффициент давления. Из формулы (33) следует, что 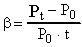 . Для всех газов
. Для всех газов 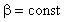 и
и 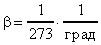 . Если газ нагреть на
. Если газ нагреть на 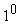 С (при V=const), то давление газа возрастет на
С (при V=const), то давление газа возрастет на 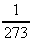 часть того давления, которое он имел при
часть того давления, которое он имел при 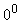 С.
С.
На рис.10 изображен график зависимости давления газа от температуры t.
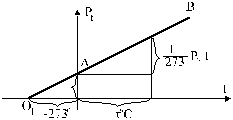
Рис. 10
Если продолжить прямую AB до пересечения ее с осью x ( точка 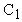 ), то значение абциссы этой определиться из формулы (33), если
), то значение абциссы этой определиться из формулы (33), если 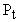 приравнять нулю.
приравнять нулю.
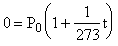
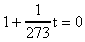 ;
; 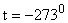 .
.
Следовательно, при температуре 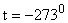 давление газа должно было бы обратиться в нуль, однако, при подобном охлаждении газ не сохранит своего газообразного состояния, а обратиться в жидкость и даже в твердое тело. Температура
давление газа должно было бы обратиться в нуль, однако, при подобном охлаждении газ не сохранит своего газообразного состояния, а обратиться в жидкость и даже в твердое тело. Температура 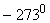 носит название абсолютного нуля.
носит название абсолютного нуля.
В случае механической смеси газов, не вступающих в химические реакции, давление смеси также определяется формулой 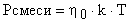 , где
, где 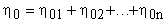 (концентрация смеси
(концентрация смеси 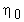 равно сумме концентраций компонентов смеси всего n - компонент).
равно сумме концентраций компонентов смеси всего n - компонент).
Закон Дальтона гласит: Давление смеси 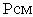 равно сумме парциальных давлений газов, образующих смесь.
равно сумме парциальных давлений газов, образующих смесь. 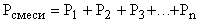 . Давления
. Давления 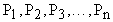 называется парциальными. Парциальное давление - это давление которое создавал бы данный газ, если бы он один занимал тот сосуд, в котором находится смесь (в том же количестве, в котором он содержится в смеси).
называется парциальными. Парциальное давление - это давление которое создавал бы данный газ, если бы он один занимал тот сосуд, в котором находится смесь (в том же количестве, в котором он содержится в смеси).
Примеры решения задач.
Пример 1. Баллон содержит 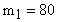 г кислорода и
г кислорода и 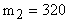 г аргона. Давление смеси
г аргона. Давление смеси 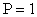 МПа, температура
МПа, температура 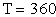 К. Принимая данные газы за идеальные, определить V баллона.
К. Принимая данные газы за идеальные, определить V баллона.
Решение. По закону Дальтона давление смеси Р равно равно сумме парциальных давлений кислорода и аргона, входящих в состав смеси. 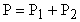 . По уравнению Менделеева-Клапейрона, парциальные давления кислорода
. По уравнению Менделеева-Клапейрона, парциальные давления кислорода 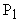 и аргона
и аргона 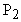 выражаются формулами :
выражаются формулами : 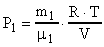 и
и 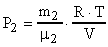 ; где
; где
V - объем баллона,
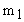 - масса кислорода,
- масса кислорода,
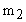 - масса аргона,
- масса аргона,
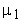 - молярная масса кислорода,
- молярная масса кислорода,
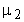 - молярная масса аргона,
- молярная масса аргона,
Т - температура смеси,
R - универсальная газовая постоянная.
Давление смеси газов 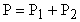 если
если
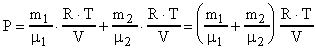 . Откуда объем баллона
. Откуда объем баллона 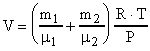 .
.
Расчет в СИ : 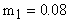 кг;
кг; 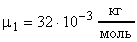 ;
; 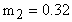 кг;
кг; 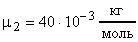 ;
; 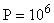 Па;
Па; 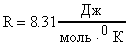 ;
; 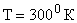 .
.
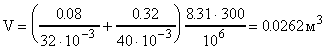 или V=26.2 л.
или V=26.2 л.
Пример 2. Во сколько раз изменится давление гелия, если его объем уменьшим в три раза, а средняя кинетическая энергия движения молекул увеличится в два раза.
Решение. Пусть объем гелия в первом состоянии 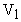 ; во втором состоянии -
; во втором состоянии - 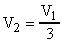 . Средняя кинетическая энергия поступательного движения в первом состоянии -
. Средняя кинетическая энергия поступательного движения в первом состоянии - 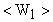 ; а во втором состоянии -
; а во втором состоянии - 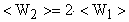 . Согласно основному уравнению молекулярно-кинетической теории
. Согласно основному уравнению молекулярно-кинетической теории 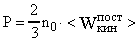 ,
, 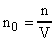 ; n - общее число молекул, которое остается постоянным; V- объем газа. Запишем уравнение для двух состояний газа
; n - общее число молекул, которое остается постоянным; V- объем газа. Запишем уравнение для двух состояний газа 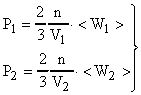 или, заменяя
или, заменяя 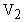 и
и 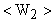 систему уравнений запишем в виде:
систему уравнений запишем в виде:
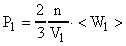 (А),
(А),
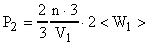 (В),
(В),
Разделим формулу (В) на формулу (А): 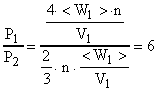 .
.
Давление гелия увеличилось в 6 раз.
Пример 3. Найти плотность воздуха при нормальных условиях.
Решение. Используем формулу (28) 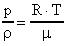 . Откуда
. Откуда 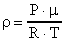 .
.
Расчет в СИ:Нормальные условия:
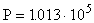 Па,
Па, 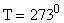 К. Для воздуха
К. Для воздуха 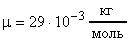 ;
;
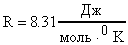
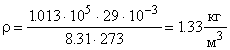 .
.
Пример 4. В сосуде под давлением 1 МПа и при температуре 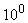 С находиться 11 г углекислого газа и 14 г азота. Найти молекулярную массу смеси и объем сосуда.
С находиться 11 г углекислого газа и 14 г азота. Найти молекулярную массу смеси и объем сосуда.
Решение. Молекулярную массу смеси 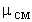 определяем из формулы:
определяем из формулы:
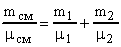 . Откуда
. Откуда 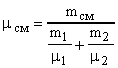 . Так как
. Так как 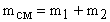 ,
,
то 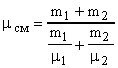 .
.
Расчет в СИ:
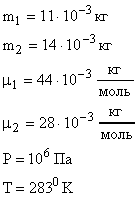
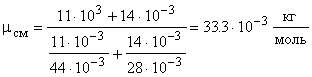 .
.
Объем сосуда найдем из уравнения Менделеева-Клапейрона
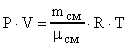 , где
, где 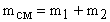
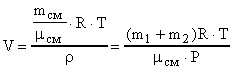 ;
; 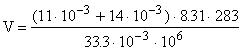 ;
;
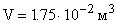

Пример 5.Компрессор засасывает из атмосферы каждую секунду 3 л воздуха, которые подаются в баллон емкостью 45 л. Через какое время давление в баллоне будет превышать атмосферное в 9 раз?
Дано: Решение:
V0= 3 л = 3*10-3 м3
V2= 45 л = 45*10-3 м3 Рассмотрим два состояния газа.
Р2=9*Р1 Первое состояние - газ находится в атмосфере в
свободном состоянии, занимая объем
t - ? V1= V0* t , где t - время накачивания,
Р1 - атмосферное давление.
Второе состояние - газ заключили в сосуд объемом V2 и давление при этом равно Р2. По закону Бойля-Мариотта (при Т=const) имеем:
Р1*V1 = Р2*V2 или, заменяя V1 и Р2, запишем:
Р1*V0*t = 9*Р1V2. Откуда 19.06.97t = 9V2/V0.
Расчет: t = 9*45*10-3/3*10-3 = 135 c.
Пример 6.Сколько молекул воздуха находится в 1 см3 при 100С, если воздух в сосуде откачан до давления 1.33 мкПа?
Дано: Решение:
V = 1 см3 = 10-6 м3 Число молекул воздуха можно найти
Т = 283 К n = (m/)NA, где NA - число Авагадро.
Р = 1.33 мкПа = 1.33*10-6 Па Число молей в 1 см3 можно определить из
уравнения Менделеева-Клаперона:
n = ? P*V = (m/) R*T. Откуда m/ =
Окончательно имеем: n = NA (P*V)/(R*T)
Расчет в СИ: n = 6/02*1023(1.33*10-6*10-6)/(8/31*283)=3/4*108
Пример 7.В озере на глубине 100 м при температуре 80С находится в равновесии шар массой 40 г, наполненный воздухом. Найти массу воздуха внутри шара, если атмосферное давление 99.7 кПа. Шар считать тонкостенным, изготовленным из резины.
Дано: Решение:
h = 100 м F На шар, погруженный в воду,
Т = 281 К действует сила тяжести Р = mg;
m = 40 г = 4*10-2 кг выталкивающая сила воды
Рат = 103 кг/м3 P = mg F=*g*V, где -плотность воды,
m1 - ?
а V= m/ (объем шара). Массу воздуха внутри шара найдем из уравнения Менделеева-Клаперона:
m1 = (*Р*V)/R*T , где Р = Рат+ Ргидр.
Ргидр= *g*h (гидравлическое давление на глубине h). Окончательно получаем:
m1 = [*(Рат+ *g*h)*m]/(R*T*)/
Расчет: m1 = [29*10-3(99/7*103+103*9/8*102)*4*10-2]/8.31*281*1035.36*10-4 кг
Пример 8.Определить плотность смеси, состоящей из 4 г водорода и 32 г кислорода, при температуре 70С и давлении 93 кПа.
Дано: Решение:
m1 = 4 u = 4*10-3 кг По закону Дальтона давление смеси Р = Р1 + Р2,
1 = 2*10-3 кг/моль где Р1 и Р2 - порциальные давления водорода и
2 = 32*10-3 кг/моль кислорода при данных условиях. Для каждого
Р = 93 кПа = 93*103 Па из газов запишем уравнение Менделеева -
Т = 280 К Клапейрона: Р1*V1 = (m1/1)R*Т1 и
R = 8.31 Дж/моль 0К Р2*V2 = (m2/2)R*Т2 по условию
задачи V1 = V2 = V и Т1 = Т2 = Т.
- ? Тогда для водорода Р1*V = (m1/1)R*Т. Откуда
1 = (m1*R*T)/(1*V).
Аналогично для кислорода получим 2 = (m2*R*T)/(2*V).
Окончательно имеем: = (m1*R*T)/(1*V) + (m2*R*T)/(2*V) =
(R*T/V)( m1/1+ m2/2). Откуда
V = (R*T/) (m1/1+ m2/2)
Плотность смеси газов = m/V = (m1+m2)/V. Заменив объем, найдем
= (m1+m2)*P/[R*T*( m1/1+ m2/2)]
=(4*10-3+32*10-3)*93*103/[8/31*280(4*10-3/2*10-3 + 32*10-3/32*10-3)]0.48 кг/м3.
Пример 9.Посередине запаянного с обеих сторон капилляра, расположенного горизонтально, находится столбик ртути длиной 10 см. Если капилляр поставить вертикально, то столбик ртути сместится на 15 см. Длина капилляра 1 м. До какого давления был откачан капилляр?
Решение:
В обоих концах капилляра (верхней части и нижней части, первоначально воздух занимал объем V0 = (L - h)S/2, где S - площадь поперечного сечения капилляра: Р0 - давление воздуха (в верхней и нижней частях капилляра).
Когда трубку поставили вертикально, то (см. рис) объем воздуха в верхней части капилляра стал V1 = [(L - h )/2 + l) S = (L - h + 2 l)S/2, а давление Р1. В нижней части капилляра объем стал V2 = [(L - h)/2 - l) S = (L - h - 2l) S/2, а давление Р2.
Для верхней части капилляра запишем закон Бойля-Мариотта:
P0V0 = P1V1 или P0(L - h)S/2 = P1(L - h + 2l)S/2
P0(L - h) = P1(L - h + 2l) (A)
Для нижней части капилляра запишем закон Бойля-Мариотта P0V0 = P2V2 или P0(L - h)S/2 = P2(L - h - 2l)S/2.
P0(L - h) = P2(L - h - 2l) (B)
Известно, что столбик ртути находится в равновесии, если давление воздуха в нижней части капилляра Р2 равно сумме давлений воздуха в верхней части капилляра Р1 и гидростатического давления столбика ртути Ргидр = gh, ( - плотность ртути), т.е. Р2 = Р1 + Ргидр = Р1 + gh.
Сравнивая формулы (А) и (В), имеем:
P1 (L - h + 2l) = P2(L - h - 2l) (C)
В формуле (С) заменим P2.
P1(L - h + 2l) = (P1 + gh) (L - h - 2l). Выразим P1.
P1(L - h + 2l) = P1 (L - h - 2l) + gh (L - h - 2l),
P1[(L - h + 2l - (L - h - 2l)] = gh (L - h - 2l),
P1 4l = gh (L - h - 2l),
P1 = gh (L - h - 2l)/(4l).
Найденное значение Р1 подставим в формулу (А),
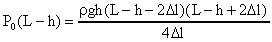 . Откуда найдем Р0
. Откуда найдем Р0
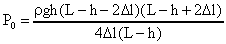 или
или 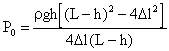 .
.
Расчет в СИ: h = 10 см = 0.1 м, = 13.6*103 кг/м3, g = 9.8 м/с2, L = 1 м, l = 15 см = 15*10-2 м.
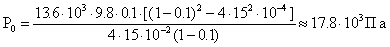 .
.
Пример 10.Водолазный колокол высотой h = 3 м с постоянным поперечным сечением опускается в море на глубину H = 80 м. Определить, до какой высоты h0 поднимется вода в колоколе, когда он достигнет глубины H, если температура у поверхности воды t1 = 20o C, а на глубине Н температура t2 = 7o C. Определить, до какого давления Р0 надо довести воздух, нагнетаемый в колокол, чтобы плотностью удалить из колокола воду. Плотность морской воды = 1030 кг/м3.
Решение:
Так как масса воздуха в колоколе при погружении не изменяется, то для этого процесса (для двух положений колокола: у поверхности воды и на глубине Н) запишем уравнение Менделеева-Клапейрона дважды:
Откуда 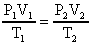 (А), сечение S колокола постоянно по высоте, поэтому V1 = hS, V2 = (h - h0)S. С учетом этого уравнения (А) запишем в виде
(А), сечение S колокола постоянно по высоте, поэтому V1 = hS, V2 = (h - h0)S. С учетом этого уравнения (А) запишем в виде
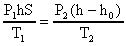 (В)
(В)
Знаем, что P1 = Pатм и Р2 = Ратм + gН.
Величина (gh) - гидростатическое давление воды на глубине Н; Ратм - атмосферное давление. После замены Р1 и Р2 в формуле (В) получим выражение
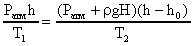 , откуда
, откуда
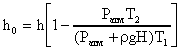 .
.
Расчет в СИ: Pатм = 1.013*105 Па; T1 = 293 K; T2 = 280 K; = 1030 кг/м3; g = 9.8 м/с2; Н = 80 м; h = 3 м.
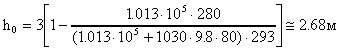 .
.
Давление Р0 воздуха для полного вытеснения воды из колокола, найдем по закону Бойля-Мариотта, учитывая, что температура воздуха в колоколе в процессе вытеснения воды не изменяется, т.к. глубина погружения колокола в этом процессе остается постоянной.
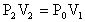 или (после замены P2, V1, V2)
или (после замены P2, V1, V2)
(Ратм + gh)(h - h0)S = P0hS
(Ратм + gh)(h - h0) = P0h. Откуда
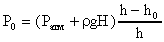 .
.
Полагая h0 = 0, получим:
Р0 = (Ратм + gH) = (1.013*105 + 1030*9.8*80) Па
P0 9.1*105 Па 9 атм.
11.Задачи для самостоятельного решения
1. Определить количество молекул воздуха в комнате 8х5х4 м3 при температуре 100С и давлении 78 см.рт.ст. Ответ: 40,81026.
2. Резиновый шар содержит 2 л воздуха при температуре 200С и атмосферном давлении 780 мм.рт.ст. Какой объем займет воздух, если шар опустить в воду, имеющую температуру 40С, на глубину 10м? До какого давления надо довести воздух, чтобы его объем остался неизменным? Ответ: 0,97 л; 1606 мм.рт.ст.
3. Газ сжат изотермически от V1 = 8л до V2 = 6л. Давление при этом возросло на p = 4кПа. Каково было первоначальное давление? Ответ: 12 кПа.
4. Газ нагрет от 270С до 390С. На сколько процентов увеличится объем, если давление газа постоянно? Ответ: на 0,4 %.
5. Открытую с обеих сторон стеклянную трубку длиной 60 см опускают на 1/3 длины в сосуд с ртутью. Затем, закрыв верхний конец, трубку вынимают из ртути. Какой длины столбик ртути останется в трубке? Атмосферное давление 105Па. Ответ: 18 см.
6. Воздушный шар объемом 1000 м3 наполнен водородом при температуре 2930К. При неизменном давлении температура поднялась до 3130К, благодаря чему вышел излишек газа. Найти объем этого излишка. Ответ: 70 м3.
7. Летчик, находясь на земле, при каждом дыхании при нормальных условиях вдыхает 1 г кислорода. Какое количество кислорода вдыхает летчик, поднявшись на высоту, где давление воздуха 400 мм.рт.ст? Изменением температуры воздуха пренебречь. Ответ: 0,53 г.
8. Определить плотность смеси, состоящей из 4 г водорода и 32 г кислорода при температуре 70С и давлении 93 кПа. Ответ: 0,48 кг/м3.
9. Сколько молекул воздуха находится в 1 см3 сосуда при 100С, если воздух в сосуде откачан до давления 1,33 мкПа? Ответ: 3,4108.
1. Теплопередача
Теплопередача (теплообмен) - это процесс обмена энергией между системой и окружающими ее телами; при этом нет изменения внешних параметров состояния системы (P, V, T). Теплопередача осуществляется либо путем непосредственного взаимодействия частиц системы с частицами среды при их случайных столкновениях (теплопроводность, конвекция), либо путем обмена электромагнитным излучением (лучеиспускание). Например, при столкновении "холодного" и "горячего" газов молекулы нагретого газа передают энергию (при случайных столкновениях) молекулам холодного газа. Вода в море в дневное время прогревается (получает энергию) за счет излучения, посылаемого Солнцем. Энергия, полученная или отданная системой в процессе теплопередачи, называется количеством тепла. Количество тепла Q измеряется в Джоулях (Дж) и является величиной скалярной. Q > 0 (положительная величина), если система получает тепло; Q < 0 (отрицательная величина), если система отдает тепло.
2. Нагревание и охлаждение веществ. Удельная теплоемкость вещества
Нагревание - процесс, при котором при подводе количества тепла Q температура вещества (твердого тела, жидкости или газа) линейно повышается (рис. 1). Количество тепла, необходимое для нагревания вещества массой m, определяется по формуле
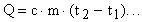 (1)
(1)
где t1 и t2 - начальная и конечная температуры нагрева; с - удельная теплоемкость вещества.
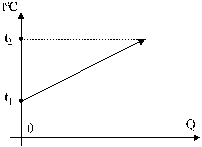
Рис.1
Охлаждение - процесс, при котором при отводе количества тепла Q температура вещества линейно понижается (рис. 2).
В обоих случаях температура тела, либо повышается, либо понижается на  градусов.
градусов.
Из формулы (1) следует
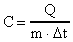 . (2)
. (2)
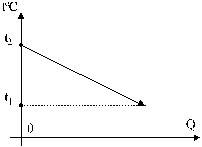
Рис. 2
Удельная теплоемкость вещества - величина, равная количеству тепла, необходимому для нагревания единицы массы вещества на один градус. Удельная теплоемкость измеряется в 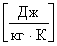 . (К - градус по шкале Кельвина). Значения С для различия веществ берут из таблицы 1.
. (К - градус по шкале Кельвина). Значения С для различия веществ берут из таблицы 1.
3. Плавление и кристаллизация. Удельная теплота плавления.
Плавление - процесс превращения твердого тела в жидкость. Этот процесс для разных веществ происходит при определенной температуре плавления (см. табл. 1). Пока твердое тело не расплавится температура плавления tпл остается постоянной (рис. 3).
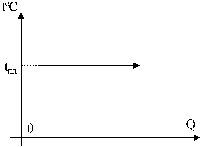
Рис. 3
Обратный процесс, при котором жидкость переходит в твердую фазу, называется кристаллизацией. Количество тепла Q, которое нужно для плавления вещества массой m, можно рассчитать как
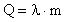 , (3)
, (3)
где - удельная теплота плавления. Удельная теплота плавления равна количеству тепла, необходимому для расплавления единицы массы вещества. Измеряется величина в Джоулях на килограмм 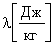 . Значения удельной теплоемкости для некоторых веществ даны в табл. 1.
. Значения удельной теплоемкости для некоторых веществ даны в табл. 1.
Таблица 1
| Вещество | Удельная теплоемкость С, кДж/кгК | Удельная теплота плавления , кДж/кг | Температура плавления tпл, С |
| Вода | 4,19 | ||
| Лед | 2,10 | ||
| Алюминий | 0,88 | ||
| Свинец | 0,13 | ||
| Сталь | 0,50 | ||
| Медь | 0,38 | ||
| Железо | 0,46 |
4. Парообразование и конденсация. Удельная теплота парообразования
Парообразование (кипение) - процесс превращения жидкости в пар. Этот процесс для разных жидкостей происходит при конкретной температуре кипения (см. табл. 2). Пока жидкость кипит, температура кипения tкип остается неизменной (рис. 4).
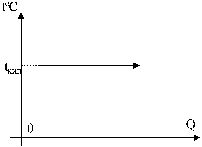
Рис. 4
Обратный процесс, при котором пар переходит в жидкость, называют конденсацией.
Количество тепла, необходимое для превращения жидкости массой m в пар:
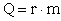 , (4)
, (4)
где r - удельная теплота парообразования
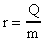 . (5)
. (5)
Удельная теплота парообразования равна количеству тепла, которое нужно для превращения единицы массы жидкости в пар. Величина r измеряется в Джоулях на килограмм 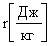 . Значения удельной теплоты парообразования некоторых жидкостей приведены в табл. 2.
. Значения удельной теплоты парообразования некоторых жидкостей приведены в табл. 2.
5. Горение топлива. Удельная теплота сгорания
Количество тепла, выделяющееся при сгорании топлива массой m рассчитывается по формуле:
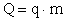 (6),
(6),
где q - удельная теплота сгорания топлива.
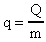 (7).
(7).
Удельная теплота сгорания топлива q численно равна количеству тепла, выделенному при сгорании единицы массы топлива. Величина q измеряется в Джоулях на килограмм 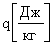 . Значения q для некоторых видов топлива представлены в табл. 2.
. Значения q для некоторых видов топлива представлены в табл. 2.
Таблица 2.
| Вещество | температура кипения tкип, С | Удельная теплота парообразования r, МДж/кг | Удельная теплота сгорания топлива q, МДж/кг |
| Вода | 2,26 | ||
| Спирт | 0,86 | ||
| Ртуть | 0,29 | ||
| Керосин | 0,21 | ||
| Бензин | |||
| Каменный уголь | |||
| Дерево |
6. Коэффициент полезного действия (КПД) нагревательных приборов
КПД нагревательных приборов определяется выражением
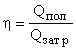 (8),
(8),
где Qпол - полезное тепло, идущее на нагревание тел, их плавление и парообразование; Qзатр - тепло, выделяющееся при сгорании топлива. Если нагревательный прибор включается в электрическую сеть, то под Qзатр понимают работу электрического тока.
7. Уравнение теплового баланса
Если между двумя или несколькими телами, входящими в изолированную систему, происходит теплообмен, то количество тепла, отданного всеми остывающими телами, равно количеству тепла, полученного всеми нагревающимися телами.
Это положение называют уравнением теплового баланса.
Пример. В сосуде, изолированном в тепловом отношении от окружающей среды, смешали m1 кг горячей воды при температуре t1C c m2 кг холодной воды при температуре t2C. Найти окончательную температуру смеси ( - буква греческого алфавита, читается: тэта).
Количество тепла, отданное остывающим телом (горячей водой):
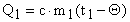 .
.
Количество тепла, полученного нагревающимся телом (холодной водой):
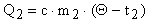
Уравнение теплового баланса
Q1 = Q2 или cm1(t1 - ) = cm2( - t2),
откуда 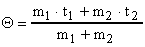 .
.
Эта формула впервые получена Г.Рихманом, членом Петербургской Академии Наук, другом и сотрудником М.В.Ломоносова.
8. Примеры решения задач
Пример 1. В калориметр, теплоемкость которого 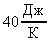 , содержащий
, содержащий
270 г воды при 12 С, опустили кусок алюминия массой 200 г, нагретый до 100С. Общая температура установилась 23С. Определить удельную теплоемкость алюминия.
Дано:
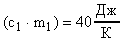 ; = 23С; t1 = 12С; c2 = 4190
; = 23С; t1 = 12С; c2 = 4190 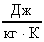 ; t2 = 12С;
; t2 = 12С;
m2 = 0,27 кг; m3 = 0,2 кг; t3 = 100С.
Найти: с3.
Решение:
Теплоемкость калориметра - это произведение удельной теплоемкости калориметра c1 на его массу m1.
В теплообмене участвуют три тела: калориметр и вода в нем. Они получают тепло и нагреваются:
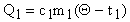 ;
;
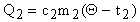 .
.
Алюминий, отдавая тепло, охлаждается:
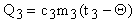 .
.
Составим уравнение теплового баланса
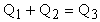 или
или 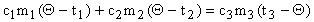 ,
,
откуда
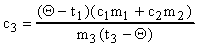 или
или 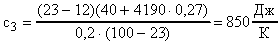 .
.
Пример 2. В сосуде теплоемкостью 600 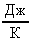 находится 0,5 кг воды и 0,2 кг льда при 0С. Какую массу водяного пара при 100С нужно впустить в воду, чтобы лед растаял и полученная вода нагревалась до 40С?
находится 0,5 кг воды и 0,2 кг льда при 0С. Какую массу водяного пара при 100С нужно впустить в воду, чтобы лед растаял и полученная вода нагревалась до 40С?
Дано:
c1m1 = 600 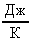 ; m2 = 0,5 кг; m3 = 0,2 кг; t1 = 0С; t2 = 100С; = 40С;
; m2 = 0,5 кг; m3 = 0,2 кг; t1 = 0С; t2 = 100С; = 40С;
r = 2,26106 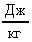 ; = 3,35105
; = 3,35105 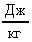 ; c2 = 4190
; c2 = 4190 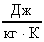 .
.
Найти:
m4 - ?
Решение:
В теплообмене участвуют сосуд, вода, лед и пар. Построим схему (рис. 5).
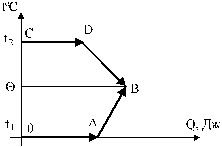
Рис. 5
На участке ОА лед плавится при 0С; Количество тепла, которое идет на плавление льда: 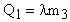 .
.
На участке АВ вода, полученная при плавлении льда, сосуд и вода в нем массой 0,5 кг нагреваются. Количество тепла, которое идет на их нагревание:
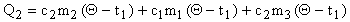 .
.
На участке CD пар конденсируется, отдавая количество тепла: 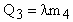
На участке DB вода, полученная при конденсировании пара, охлаждается и отдает количества тепла 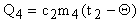 .
.
Запишем уравнение теплового баланса:
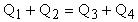 или
или 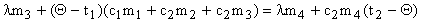 .
.
Откуда:
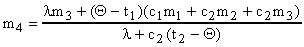 ;
;
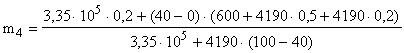 ;
;
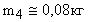 .
.
Пример 3. На сколько градусов повысится температура 10 кг воды, взятой при 12С, если в нее влить 5 кг расплавленного свинца при температуре плавления?
Дано:
m1 = 10 кг; с1 = 4190 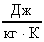 ; t1 = 12С; m2 = 5 кг; = 2,3104
; t1 = 12С; m2 = 5 кг; = 2,3104 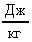 ; c2 = 130
; c2 = 130 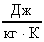 ; tпл = 327С.
; tпл = 327С.
Найти:
t - ?
Решение:
Построим схему происходящих тепловых процессов (рис. 6)
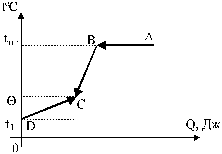
Рис. 6
Когда свинец в расплавленном состоянии вливают в холодную воду, то он сначала будет затвердевать (участок АВ).
При этом выделится количество тепла 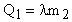 , где - удельная теплота плавления свинца. Затем свинец будет остывать до общей температуры ; при этом выделится количество тепла
, где - удельная теплота плавления свинца. Затем свинец будет остывать до общей температуры ; при этом выделится количество тепла 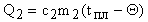 (участок ВС).
(участок ВС).
Холодная вода будет нагреваться от t1 до и получит количество тепла 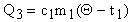 (участок DC).
(участок DC).
Запишем уравнение теплового баланса:
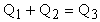 или
или
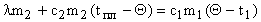 .
.
Откуда найдем .
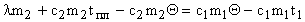 ;
;
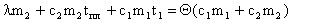 ;
;
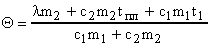 ;
;
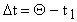 или
или
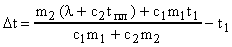 .
.
Подставим числовые значения
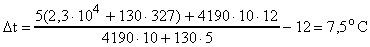 .
.
Пример 4. В латунный колориметр массой 128 г, содержащий 240 г воды при 8,4С, опущено металлическое тело массой 192 г, нагретое до 100С. Окончательная температура, установившаяся в калориметре, 21,5С. Определить удельную теплоемкость испытуемого тела.
Дано:
c2 = 4190 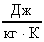 ; m1 = 128 г = 0,128 кг; m2 = 240 г = 0,24 кг; t1 = t2 = 8,4С; m3 = 192 г = 0,192 кг; t3 = 100С; = 21,5С; с1 = 380
; m1 = 128 г = 0,128 кг; m2 = 240 г = 0,24 кг; t1 = t2 = 8,4С; m3 = 192 г = 0,192 кг; t3 = 100С; = 21,5С; с1 = 380 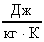 .
.
Найти:
с3 - ?
Решение:
В теплообмене участвуют три тела: калориметр, вода и металл. Вода и калориметр получают количество тепла: 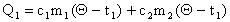 .
.
Металлическое тело отдает тепло:
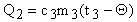 .
.
Запишем уравнение теплового баланса:
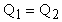 или
или 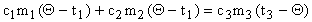 .
.
Откуда
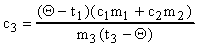 ;
; 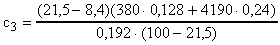 ;
; 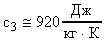 .
.
Пример 5. В один килограмм воды при 20С бросают кусок железа массой 100 г, нагретый до 500С. Вода нагрелась при этом до 24С и часть ее обратилась в пар. Найти массу пара.
Дано:
m1 = 1 кг; c1 = 4190 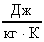 ; t1 = 20С; = 24С; m2 = 100 г = 0,1 кг;
; t1 = 20С; = 24С; m2 = 100 г = 0,1 кг;
c2 = 460 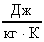 ; r = 2,26106
; r = 2,26106 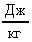 ; t3 = 500С; t2 = 100С.
; t3 = 500С; t2 = 100С.
Найти:
mx - ?
Решение:
Построим схему происходящих
