Энергия поступательного движения молекул газа

Кинетическая энергия, которой обладают n молекул газа при некоторой температуре Т вследствие своего поступательного движения равна:

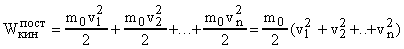
или .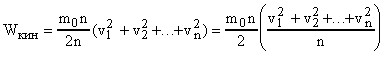

Так как 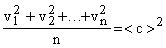, то

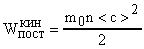. (20)

Из основной формулы кинетической теории (12) следует, что 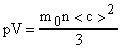. (21)

Разделив (20) на (21), получим:

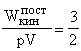или 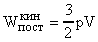. (22)

Заменим 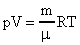и запишем

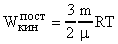. (23)

Если газ взят в количестве одного моля 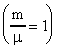, то:

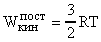. (24)

Средняя кинетическая энергия поступательного движения одной газовой молекулы:

.

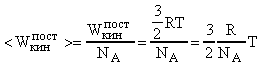Так как 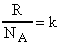, то 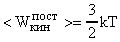. (25)

При одной и той же температуре средняя энергия поступательного движения молекул любого газа одна и та же.

Примеры решения задач

Пример 1. Определить число n молекул, содержащихся в объеме V = 1 мм³ воды и массу m₀ молекулы воды.

Решение:

Число молекул n, содержащихся в теле некоторой массы m:

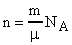, где  - молярная масса. Так как 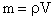, где  - плотность воды, то: .

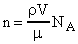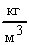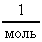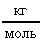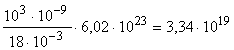Расчет в СИ: V = 10^-9 м³;  = 10³ ; N_A = 6,0210²³ ;  = 1810^-3 ; n = молекул.

m₀ подсчитываем по формуле (3) ; .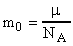

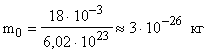Пример 2.Определить число молекул содержащихся в 10 г азота.

Решение:

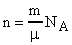
Расчет в СИ:

m = 10 г = 10^-2 кг;  = 2810^-3 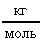; N_A = 6,0210²³ 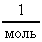; 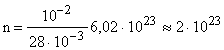молекул.

Пример 3.Вычислить среднюю квадратичную скорость движения молекул водорода при 0⁰С.

Решение:

Среднюю квадратичную скорость рассчитаем по формуле (17): .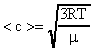

Расчет в СИ: R = 8,31 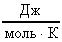;  = 210^-3 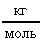; Т = 273 К.

.

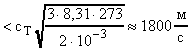Проверим размерность

.

.

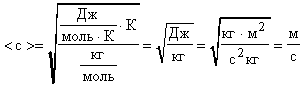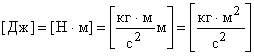Пример 4.Вычислить наиболее вероятную среднюю квадратичную и среднюю арифметическую скорости молекул азота при температуре 420 К.

Решение:

При расчетах используем формулы (18), (17) и (19).

В СИ: Т = 420 К;  = 2810^{-3 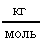;} R = 8,31 .

.

.

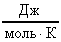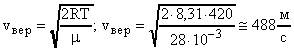
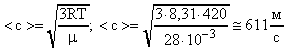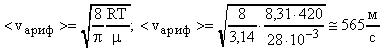Пример 5.Чему равна средняя квадратичная скорость движения молекул воздуха при температуре 27⁰С?

Решение:

Среднюю квадратичную скорость молекул воздуха вычислим по формуле (17).

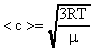. В Си:  = 2910^{-3 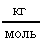(для воздуха); Т = 2730}К;

R = 8,31 .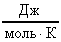

.

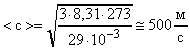Пример 6. Вычислить среднюю энергию поступательного движения молекулы газа при 27⁰С.

Решение:

Для расчета используем формулу (5).

.

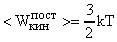В Си: К = 1,3810^-23 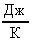; Т = 300⁰К.

^.

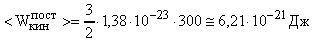Пример 7.Средняя квадратичная скорость молекул некоторого газа <c> = 450 м/с. Давление газа р = 50 кПа. Найти плотность  газа при этих условиях.

Решение:

Основное уравнение молекулярно-кинетической теории запишем в виде:

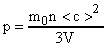. Так как 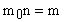(масса газа); а 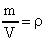(плотность газа), то 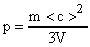или 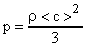. Откуда .

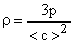Расчет в Си: р = 5010³ Па; <c> = 450 м/с.

.

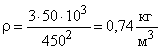Проверим размерность:

.

.

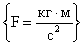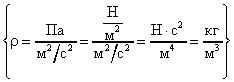Пример 8. Энергия поступательного движения молекул азота, находящегося в баллоне объемом V = 20л, 5 кДж, а средняя квадратичная скорость его молекул <c> = 210³ м/с. Найти массу m азота в баллоне и давление р под которым он находится.

Решение:

Энергия поступательного движения молекул азота может быть выражена как 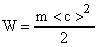, откуда 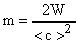. Известно, что 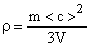(А). В формуле (А) заменим m. ; .

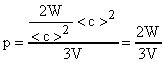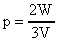Расчет в Си: V = 2010^-3 м³; W = 510³ Дж; <c> = 210³ м/с.

; .

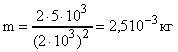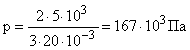Пример 9. Найти среднюю арифметическую <v_ариф>, среднюю квадратичную <c> и наиболее вероятную v_вер скорости молекул газа, который при давлении p = 40 кПа имеет плотность  = 0,3 кг/м³.

Решение:

Для расчета используем формулу (16) 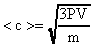(16). Так как 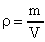и 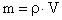, то (после замены m) получаем ; .

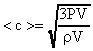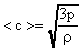Формулу (19) можно преобразовать 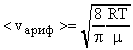(19). Для этого заменим 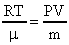или, зная, что 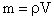, получим 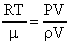; 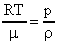. Окончательно имеем 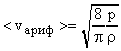. Аналогично в формуле (18) заменим величину .

, .

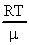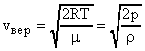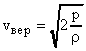Расчет в Си: p = 4010³ Па;  = 0,3 кг/м³.

; ; .

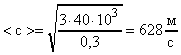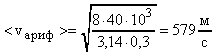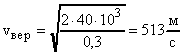Пример 10. Средняя квадратичная скорость молекул некоторого газа при нормальных условиях <c> = 461 м/с. Какое число молекул содержит единица массы этого газа?

Решение.

Известно, что массу одной молекулы можно найти 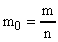(А), где m - масса всех молекул, а n - число молекул. По условию задачи нужно определить, какое число молекул содержит единица массы газа, т.е. величину 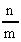. Из формулы (А) выразим 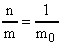(В). Согласно формуле (17) 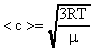. Откуда 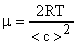(С). Массу одной молекулы можно определить иначе (см. формулу (3)). 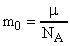. Заменим , используя выражение (С).

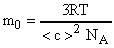. Так как 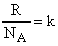, то 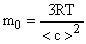. Найденное значение m₀ подставим в равенство (В). Окончательно получим:

.

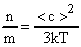Расчет в си:

нормальные условия: 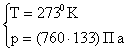; <c> = 461 м/с; k = 1,310^-23 .

.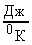
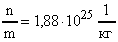