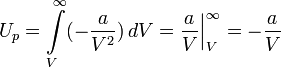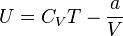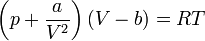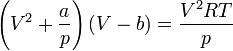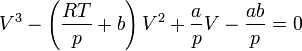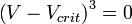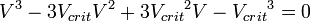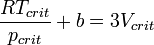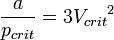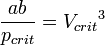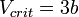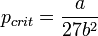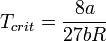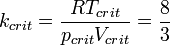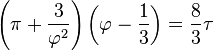Межмолекулярное взаимодействие.

Межмолекулярное взаимодействие — взаимодействие между молекулами и/или атомами, не приводящее к образованию ковалентных (химических) связей.

Межмолекулярное взаимодействие имеет электростатическую природу. Предположение о его существовании было впервые использовано Я. Д. Ван-дер-Ваальсом в 1873 году для объяснения свойств реальных газов и жидкостей. В наиболее широком смысле под ним можно понимать такие взаимодействия между любыми частицами (молекулами, атомами, ионами), при которых не происходит образования химических, то есть ионных, ковалентных или металлических связей. Иными словами, эти взаимодействия существенно слабее ковалентных и не приводят к существенной перестройке электронного строения взаимодействующих частиц.

На больших расстояниях преобладают силы притяжения, которые могут иметь ориентационную, поляризационную (индукционную) и дисперсионную природу (см. подробнее в статьях Силы Ван-дер-Ваальса и Дисперсионные силы). При усреднении по вращению частиц, происходящему вследствие теплового движения, потенциал межмолекулярных сил обратно пропорционален шестой степени расстояния, а ион-дипольных (как с постоянным, так и с наведенным диполем) — четвёртой степени. На малых расстояниях начинают преобладать силы отталкивания электронных оболочек частиц. Особым случаем является водородная связь — возникающее на малом расстоянии взаимодействие между атомом водорода одной молекулы и электроотрицательным атомом другой, когда эти атомы несут достаточно большой эффективный заряд.

Упаковку частиц и расстояние между ними в конденсированной фазе, определяющиеся равновесием между притяжением и отталкиванием, можно предсказать, исходя из ван-дер-ваальсовых радиусов составляющих молекулы атомов (ионных в случае ионов): расстояния между атомами разных молекул не должны превышать суммы радиусов этих атомов. Для моделирования межмолекулярных взаимодействий используют эмпирические потенциалы, среди которых наиболее известны потенциалы Леннард-Джонса (отталкивание описывается двенадцатой степенью обратного расстояния, притяжение — шестой) и Бакингема (с более физически обоснованным экспоненциальным отталкиванием), из которых первый более удобен для расчетов. В конденсированной фазе, где мультипольное разложение для молекул плохо применимо из-за близости молекул друг к другу, может применяться метод атом-атомных потенциалов, основанный на тех же потенциалах, но уже для парных взаимодействий атомов и с добавкой кулоновских членов, описывающих взаимодействие их эффективных зарядов.

Ван-дер-ваальсова связь (межмо­лекулярное взаимодействие). Все вещества в зависимости от внешних условий (температуры и давления) могут существовать в различных агрегатных состояниях. Так, при низких темпера­турах оказывается возможным «согласованное» движение электро­нов, при котором у молекулы могут воз­никать наведенные диполи без переда­чи атомами электронов, и между ними возникают так называе­мые индукционные силы притяжения. Такой вид взаимодействия называется ван-дер-ваальсовой связью. Энергия такой связи намного (в сот­ни раз) меньше энергий ковалентных, ионных или металлических. Вандерваальсовы силы обусловливают притяжение молекул и агрегацию вещества, превращение газообраз­ного вещества в жидкое и далее в твердое состояние.

Связь между молекулами может осуществляться как электростатическим, так и донорно-акцепторным взаимодействием, что обусловливает разнообразие сложных соединений и их характерных свойств – так образуются комплексные соединения, рассматриваемые в отдельной главе.

Уравнение Ван-дер-Ваальс.

Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия 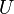становится функцией не только температуры, но и объёма.

Уравнение Ван-дер-Ваальса — это одно из широко известных приближённых уравнений состояния, имеющее компактную форму и учитывающее основные характеристики газа с межмолекулярным взаимодействием^[1].

ермическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

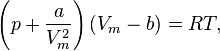
где

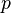• — давление,
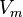• — молярный объём,
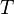• — абсолютная температура,
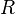• — универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка 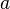учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка 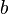— объем молекул газа.

Для 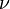молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

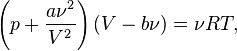
где

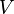• — объём.

· Потенциальная энергия межмолекулярных сил взаимодействия вычисляется как работа, которую совершают эти силы, при разведении молекул на бесконечность:

• 

· Внутренняя энергия газа Ван-дер-Ваальса складывается из его кинетической энергии (энергии теплового движения молекул) и только что нами посчитанной потенциальной. Так, для одного моля газа:

• 

· где 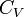— молярная теплоёмкость при постоянном объёме, которая предполагается не зависящей от температуры.

· Критические параметры

· Критическими параметрами газа называются значения его макропараметров (давления, объёма и температуры) в критической точке, т.е. в таком состоянии, когда жидкая и газообразная фазы вещества неразличимы. Найдем эти параметры для газа Ван-дер-Ваальса, для чего преобразуем уравнение состояния:

• 
• 

· Мы получили уравнение третьей степени относительно .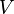

• 

· В критической точке все три корня уравнения сливаются в один, поэтому предыдущее уравнение эквивалентно следующему:

• 
• 

· Приравняв коэффициенты при соответствующих степенях 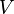, получим равенства:

• 
• 
• 

· Из них вычислим значения критических параметров...

• 
• 
• 

· ...и критического коэффициента:

• 

· Приведённые параметры

· Приведённые параметры определяются как отношения

• 

· Если подставить в уравнение Ван-дер-Ваальса 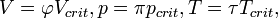получится приведённое уравнение состояния.

• 

· Стоит отметить, что если вещества обладают двумя одинаковыми приведёнными параметрами из трёх, то и третьи приведённые параметры у них совпадают.

· Недостатки уравнения Ван-дер-Ваальса^[2]

• 1. Для реальных веществ
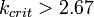
• 2. Для реальных веществ 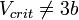(скорее, )
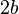• 3. Уравнение Ван-дер-Ваальса расходится с экспериментом в области двухфазных состояний.

Экспериментальные изотермы

Реальные газы отличаются от идеальных тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой сложными силами взаимодействия. При высоких давлениях и достаточно низких температурах реальные газы конденсируются, т. е. переходят в жидкое состояние, чего принципиально не может быть с идеальными газами.

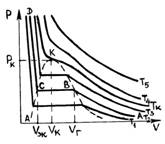
В 1861 году ирландский физик-химик Т. Эндрюс экспериментально исследовал зависимость давления углекислого газа от объема при изотермическом сжатии. На рис. 1 схематично представлены результаты опытов, подобных опытам Т. Эндрюса. Рассмотрим изотерму АВСD.

рис. 1

На участке АВ уменьшение объема, занятого газом, сопровождается увеличением давления сначала обратно пропорционально объему, затем все медленнее.

В точке В начинается конденсация газа и продолжается при постоянном давлении, называемом давлением насыщенных паров, до точки С. В точке С процесс конденсации газа заканчивается, при дальнейшем уме-ньшении объема осуществляется сжатие жидкости (участок СD), сопровождающееся быстрым ростом давления, свидетельствующее о том, что жидкость слабо сжимаема. При уменьшении давления, действующего на жидкость, вещество пройдет те же состояния в обратном порядке: оно расширится по пути DС до точки кипения, произойдет испарение (путь СВ), а затем получившийся пар расширится до исходного давления (точка А).

На участке ВС не только давление, но и температура постоянны. Крайним точкам отрезка ВС соответствуют однофазные состояния вещества: точке С (объем 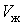) – жидкое, а точке В (объем 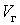) – газообразное. В промежуточном двухфазном состоянии с объемом V часть вещества с количеством молей 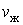находится в жидком, а часть с количеством молей 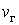– в газообразном состоянии. Определим отношение количества молей жидкой и газообразной фаз в объеме V .

Объем одного моля жидкой и газообразной фаз вещества соответственно равны:

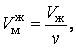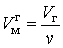(5.1.1)

Объем V содержит 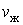молей жидкой фазы и 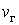молей газообразной фазы, поэтому этот объем можно представить в виде суммы объемов жидкой и газообразной фаз следующим образом:

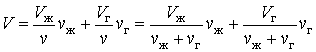(5.1.2)

После простых преобразований из выражения (5.1.2) находим искомое отношение

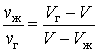(5.1.3)

Умножая числитель и знаменатель левой части выражения (5.1.3) на молярную массу вещества, получим аналогичное отношение для масс жидкой и газообразной фаз:

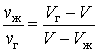(5.1.4)

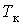На рис. 1 представлены изотермы газа при различных температурах Из рисунка видно, что с ростом температуры горизонтальный участок, соответствующий двухфазному состоянию вещества, уменьшается и при некоторой температуре , называемой критической, стягивается в точку K . Изотерма, соответствующая температуре , называется критической изотермой, точка K которой является точкой перегиба.

> T_к.

Фазовые переходы 1 и 2 рода

Фазовые переходы второго рода — фазовые переходы, при которых вторые производные термодинамических потенциалов по давлению и температуре изменяются скачкообразно, тогда как их первые производные изменяются постепенно. Отсюда следует, в частности, что энергия и объём вещества при фазовом переходе второго рода не изменяются, но изменяются его теплоёмкость, сжимаемость, различные восприимчивости и т. д.

Изменение симметрии

Фазовые переходы второго рода сопровождаются изменением симметрии вещества. Изменение симметрии может быть связано со смещением атомов определённого типа в кристаллической решётке, либо с изменением упорядоченности вещества.

В большинстве случаев, фаза, обладающая большей симметрией (т. е. включающей в себя все симметрии другой фазы), соответствует более высоким температурам, но существуют и исключения. Например, при переходе через нижнюю точку Кюри в сегнетовой соли, фаза, соответствующая меньшей температуре, обладает ромбической симметрией, в то время как фаза, соответствующая большей температуре, обладает моноклинной симметрией.

Для количественной характеристики симметрии при фазовом переходе второго рода вводится параметр порядка, принимающий отличные от нуля значения в фазе с большей симметрией, и тождественно равный нулю в неупорядоченной фазе.

Теория среднего поля

Основная статья: Теория Ландау

Теория среднего поля – самый первый и простейший способ теоретического описания критических явлений. Для этого производится линеаризация многочастичного гамильтониана взаимодействия, то есть фактически, он заменяется на одночастичный гамильтониан с некоторым эффективным самосогласованным полем. Таким образом мы переходим от близкодействия к дальнодействию, то есть к взаимодействию с формально бесконечным радиусом. Также мы пренебрегаем корреляционными эффектами.

Применение теории среднего поля для описания фазовых переходов фактически эквивалентно применению теории Ландау, то есть разложению функционала свободной энергии по степеням параметра порядка около критической точки.

При описании фазовых переходов, эффективное поле обычно принимается пропорциональным параметру порядка. Как правило, множителем пропорциональности является средняя энергия взаимодействия частиц системы. Так, в магнетике рассматривается действие на отдельный электронный спин локального магнитного поля, создаваемое соседними спинами.

Критические показатели для магнетика в теории Ландау:

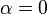
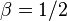
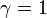
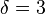
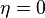
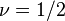
Для других систем – антиферромагнетика, бинарного сплава и системы жидкость-пар теория среднего поля даёт те же критические показатели.

Критические показатели, полученные в теории среднего поля плохо согласуются с экспериментальными значениями. Но она предсказывает полную универсальность показателей, то есть их независимость от деталей теории.

Основным недостатком теории является то, что она неприменима в тех случаях, когда существенными становятся флуктуации параметра порядка, то есть непосредственно в окрестности точки фазового перехода:Теория Ландау справедлива до тех пор, пока флуктуации в объеме с линейными размерами порядка радиуса корреляции малы по сравнению с равновесным значением параметра порядка. В противном случае термодинамический подход неприменим. Для самих точек фазового перехода теория даёт завышенные показания, а предсказываемые ей критические показатели отличаются от экспериментальных значений. Кроме того, критические показатели, согласно теории среднего поля, не зависят от размерностей пространства и параметра порядка. Для систем с размерностями d=1, d=2 теория среднего поля вообще не применима.

Гауссово приближение

В гауссовом приближении решается модель Гинзбурга-Ландау. Наивероятнейшая конфигурация ищется минимизацией блочного гамильтониана. Отклонения от наивероятнейшей конфигурации считаются независимыми и распределёнными по гауссу.

Блочный гамильтониан Гинзбурга-Ландау - простейшая форма блочного гамильтониана:

( )

( )

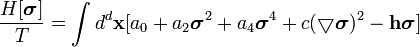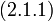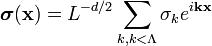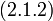В Фурье-представлении 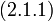имеет вид:

( )

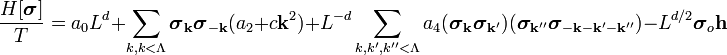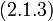Наивероятнейшая спиновая конфигурация 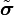, минимизирующая 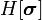, должна быть однородной, то есть градиентный член должен быть равен нулю. Таким образом,

( )

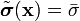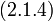Все фурье-компоненты с 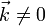равны нулю:

( )

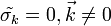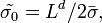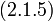Подставляя 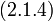в 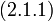, получаем:

( )

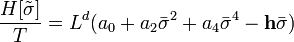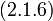Наивероятнейшее значение, , найдём, минимизируя :

( )

( )

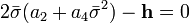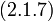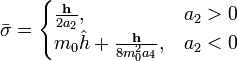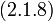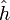- единичный вектор в направлении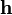

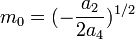
Если рассматривать только наивероятнейшее значение, то мы будем иметь дело с теорией среднего поля Ландау, поэтому нужно рассмотреть отклонения от наивероятнейшей конфигурации в гауссовом приближении. Случа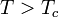и и 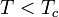рассмотрим отдельно.

• 

В этом случае 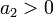и для простоты положим 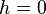. В представлении 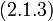оставим члены не выше второго порядка по :

( )

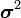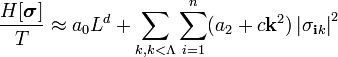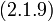Мерой отклонения от наивероятнейшего значения служит 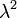- квадрат полуширины Гауссова распределения 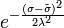. В данном случае:

• 

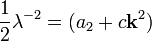
В этом случае остаётся ненулевой величиной. Считаем конечным, но малым вектором. Разложим по степеням 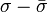и оставим члены до второго порядка включительно. Используем формулы и :

( )

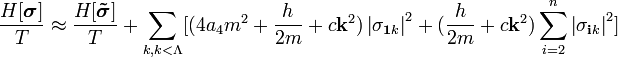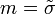- намагниченность.

В данном случае,

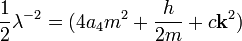
и

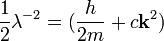
Гауссово приближение описывает многие важные свойства критических явлений. Предсказываемые ей критические индексы –

,

,

,

,

,

.

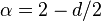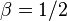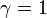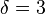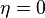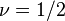Все показатели, полученные в гауссовом приближении совпадают с таковыми из теории среднего поля. Но теперь теплоемкость не только имеет разрыв при 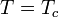, но и расходится при 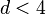. Причиной этой расходимости служат флуктуации мод с малыми 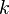. В теории Ландау мы пренебрегаем модами с .

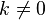Мы учитываем флуктуации лишь до второго порядка, считая, что они малы. Но вблизи критической точки флуктуации сильно возрастают, поэтому гауссово приближение становится неприменимым.

Флуктуационная теория

Флуктуационная теория фазовых переходов второго рода работает вне области применимости теории Ландау и находит критические показатели и общие закономерности фазовых переходов второго рода. В этой теории аномальное поведение физических величин вблизи точки фазового перехода связывается с сильным взаимодействием флуктуаций параметра порядка, радиус корреляции которых неограниченно растёт и обращается в бесконечность в самой точке фазового перехода. Вследствие этого, система не может быть разделена на статистически независимые подсистемы, и флуктуации на всех масштабах оказываются негауссовыми.

Описание производится методами квантовополевой теории возмущений. Для учёта влияния флуктуаций мы возвращаемся от среднего значения параметра порядка 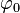к случайному полю 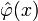с простым функционалом Ландау в качестве гамильтониана. Усреднение тогда должно производиться по всем конфигурациям случайного поля 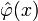в окрестности его равновесного среднего, плотность вероятности в пространстве конфигураций определяется весовым множителем (функция распределения параметра порядка ):

( )

( )

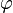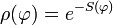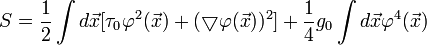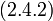Нахождение средних значений с помощью функции распределения 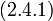требует вычисления функционального интеграла. При учёте первых двух слагаемых (Гауссово приближение) мы можем проделать это для фурье-образа 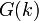парного коррелятора :

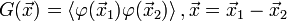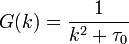
При 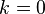эта величина имеет смысл восприимчивост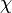и , при 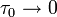она возрастает по закону:

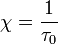
В трёхмерном случае

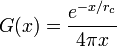
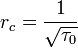- радиус корреляции неограниченно растёт при приближении к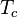

В гауссовом приближении фурье-компоненты поля 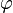статистически независимы, а для корреляторов старших порядков справедлива теорема Вика. Нелинейное слагаемое 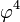в можно учесть только в виде теории возмущений, что приводит к Фейнмановской диаграммной технике с четверным взаимодействием.

Примеры фазовых переходов второго рода

• переход парамагнетик-ферромагнетик или парамагнетик-антиферромагнетик (параметр порядка — намагниченность),
• переход металлов и сплавов в состояние сверхпроводимости (параметр порядка — плотность сверхпроводящего конденсата),
• переход жидкого гелия в сверхтекучее состояние (п.п. — плотность сверхтекучей компоненты),
• переход аморфных материалов в стеклообразное состояние.