Второе начало термодинамики. Энтропия.

Обычно всякий процесс, при котором система переходит из одного состояния в другое, протекает таким образом, что нельзя провести этот процесс в обратном направлении так, чтобы система проходила через те же промежуточные состояния, и при этом в окружающих телах не произошли какие-либо изменения. Это связано с тем, что в процессе часть энергии рассеивается, например, за счет трения, излучения и т. п. Т. о. практически все процессы в природе необратимы. В любом процессе часть энергии теряется. Для характеристики рассеяния энергии вводится понятие энтропии. (Величина энтропии характеризует тепловое состояние системы и определяет вероятность осуществления данного состояния тела. Чем более вероятно данное состояния, тем больше энтропия.) Все естественные процессы сопровождаются ростом энтропии. Энтропия остается постоянной только в случае идеализированного обратимого процесса, происходящего в замкнутой системе, то есть в системе, в которой не происходит обмен энергией с внешними по отношению к этой системе телами.

Энтропия и ее термодинамический смысл:

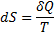
Энтропия – это такая функция состояния системы, бесконечно малое изменение которой в обратимом процессе равно отношению бесконечно малого количества теплоты, введенного в этом процессе, к температуре, при которой оно вводилось.

В конечном обратимом процессе изменения энтропии может быть подсчитано по формуле:

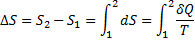
где интеграл берется от начального состояния 1 системы до конечного состояния 2.

Поскольку энтропия есть функция состояния, то свойством интеграла 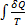является его независимость от формы контура (пути), по которому он вычисляется, следовательно, интеграл определяется только начальным и конечным состояниям системы.

• В любом обратимом процессе изменения энтропии равно 0

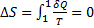(1)

• В термодинамике доказывается, что S системы совершающей необратимой цикл возрастает

ΔS > 0 (2)

Выражения (1) и (2) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то её S может вести себя любым образом.

Соотношения (1) и(2) можно представить в виде неравенства Клаузиуса

ΔS ≥ 0

т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов) либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояния 2, то изменения энтропии

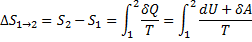
где dU и δA записывается для конкретного процесса. По этой формуле ΔS определяется с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий. Найдем изменение энтропии в процессах идеального газа.

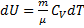
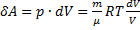
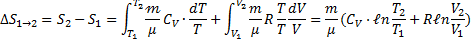
т.е. изменения энтропии S ΔS_1→2 идеального газа при переходе его из состояния 1 в состояния 2 не зависит от вида процесса.

Т.к. для адиабатического процесса δQ = 0, то ΔS = 0 => S = const, то есть адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его называют изоэнтропийным.

При изотермическом процессе (T = const; T₁ = T₂: )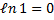

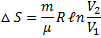
При изохорном процессе (V = const; V₁ =V₂; )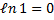

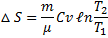
Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел входящих в систему. S = S¹ + S² + S³ + ... Качественным отличием теплового движения молекул от других форм движения является его хаотичность, беспорядочность. Поэтому для характеристики теплового движения необходимо ввести количественную меру степени молекулярного беспорядка. Если рассмотреть какое-либо данное макроскопическое состояния тела с определенными средними значениями параметров, то оно есть нечто иное, как непрерывная смена близких микросостояний, отличающихся друг от друга распределением молекул в разных частях объема и распределяемой энергией между молекулами. Число этих непрерывно сменяющих друг друга микросостояний характеризует степень беспорядочности макроскопического состояния всей системы, w называется термодинамической вероятностью данного микросостояния. Термодинамическая вероятность w состояния системы — это число способов, которыми может быть реализовано данное состояния макроскопической системы, или число микросостояний, осуществляющих данное микросостояния (w ≥ 1, а математическая вероятность ≤ 1).

За меру неожиданности события условились принимать логарифм его вероятности, взятый со знаком минус: неожиданность состояния равна = -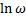

Согласно Больцману, энтропия S системы и термодинамическая вероятность связаны между собой следующим образом:

S=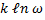

где 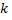- постоянная Больцмана ( 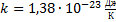). Таким образом, энтропия определяется логарифмом числа состояния, с помощью которых может быть реализовано данное микросостояние. Энтропия может рассматриваться как мера вероятности состояния т/д системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкования. Энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний реализующих данное микросостояние, тем больше энтропия. В состоянии равновесия системы - наиболее вероятного состояния системы – число микросостояний максимально, при этом максимальна и энтропия.

Т.к. реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению ее энтропии - принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной.

Второе начало термодинамики

Первое начало термодинамики, выражая закон сохранения энергии и превращения энергии, не позволяет установить направление протекания т/д процессов. Кроме того, можно представить множество процессов, не противоречащих I началу т/д, в которых энергия сохраняется, а в природе они не осуществляются. Возможные формулировки второго начало т/д:

1) закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимой процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает ΔS ≥ 0 (необратимый процесс) 2) ΔS ≥ 0 (S = 0 при обратимом и ΔS ≥ 0 при необратимом процессе)

В процессах, происходящих в замкнутой системе, энтропия не убывает.

2) Из формулы Больцмана S= 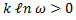, следовательно, возрастание энтропии означает переход системы из менее вероятного состояния в более вероятное.

3) По Кельвину: не возможен круговой процесс, единственным результатом которого является превращения теплоты, полученной от нагревателя в эквивалентную ей работу.

4) По Клаузиусу: не возможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Для описания т/д систем при 0 К используют теорему Нернста-Планка (третье начало т/д): энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к 0 К

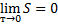
Из теоремы Нернста-Планка следует, что C_p = C_v = 0 при 0 К