Основное уравнение молекулярно- кинетической теории идеальных газов.
Это газ, состоящий из точечных материальных частиц (с конечной массой), силами взаимодействия между которыми можно пренебречь, упруго сталкивающихся между собой. Следовательно, молекулы идеального газа обладают только кинетической энергией, поскольку потенциальной энергией взаимодействия молекул можно пренебречь. Тот факт, что частицы точечные, позволяет считать, что газ занимает весь предоставленный ему объём. Иногда эту модель расширяют: идеальные твердые сферы (уже с собственным объемом), сталкивающиеся между собой по законам абсолютно упругого удара (модель твердых сфер).
Основное уравнение молекулярно-кинетической теории идеального газа связывает важный макроскопический параметр с микроскопическими характеристиками, относящимися к его структурным элементам – молекулам. Учитывая беспорядочное непрерывное движение молекул и их соударения со стенками сосуда и друг с другом, макроскопическим параметром может быть давление газа, которое связано с изменением импульса молекул.
Как известно, величина давления определяется силой, действующей нормально на единицу площади поверхности: 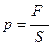 .
.
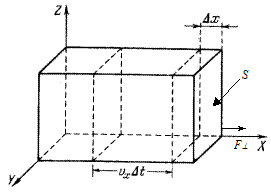 Рис. 6.2 Рис. 6.2 |
Давление газа на стенки обусловлено огромным числом столкновений молекул газа со стенками.
Согласно второму закону Ньютона 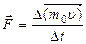
Импульс одной молекулы вдоль оси Х равен 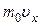 , где m0 - масса одной молекулы. Пусть в единице объема сосуда находится n молекул, из них половина движется вдоль оси Х, а другая половина – в противоположном направлении. За время Dt в слой Dx (Dx – расстояние, на котором проявляется действие молекул на стенку) слева направо входит
, где m0 - масса одной молекулы. Пусть в единице объема сосуда находится n молекул, из них половина движется вдоль оси Х, а другая половина – в противоположном направлении. За время Dt в слой Dx (Dx – расстояние, на котором проявляется действие молекул на стенку) слева направо входит 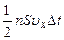 молекул.
молекул.
Каждая из них обладает импульсом 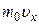 , следовательно, общий импульс, вносимый ими в слой, равен
, следовательно, общий импульс, вносимый ими в слой, равен 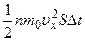 . За это же время слой покидает, двигаясь, справа налево, такое же число молекул с таким же общим импульсом, но противоположного знака. Общее изменение импульса:
. За это же время слой покидает, двигаясь, справа налево, такое же число молекул с таким же общим импульсом, но противоположного знака. Общее изменение импульса:
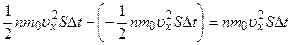 .
.
Импульс силы, действующей на стенку, площадью S, равен изменению импульса частиц 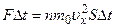 . Тогда давление на стенку, будет определяться формулой:
. Тогда давление на стенку, будет определяться формулой:
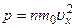 (6.1)
(6.1)
Двигаясь беспорядочно в пространстве, молекулы имеют составляющие скоростей и вдоль других осей. Полная скорость молекулы может быть выражена через её составляющие по трём независимым направлениям: 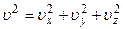 . Поскольку в движении участвует множество молекул, то необходимо использовать средние квадраты скоростей:
. Поскольку в движении участвует множество молекул, то необходимо использовать средние квадраты скоростей: 
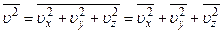 . Так как движение беспорядочное, то все три компоненты скоростей равноправны:
. Так как движение беспорядочное, то все три компоненты скоростей равноправны: 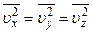 . Отсюда
. Отсюда 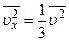 . После подстановки в уравнение (6.1) получим:
. После подстановки в уравнение (6.1) получим:
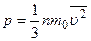 (6.2)
(6.2)
Уравнение (6.2) связывает макроскопический параметр – давление – и микроскопические параметры – массу и средний квадрат скорости молекулы, его называют основным уравнением молекулярно-кинетической теории идеальных газов. Однако, часто это уравнение используют в другом виде: 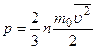 . Здесь
. Здесь 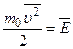 – средняя кинетическая энергия поступательного движения молекулы. Таким образом, давление идеального газа определяется средней кинетической энергией поступательного движения молекулы и является статистической величиной:
– средняя кинетическая энергия поступательного движения молекулы. Таким образом, давление идеального газа определяется средней кинетической энергией поступательного движения молекулы и является статистической величиной:
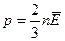 (6.3)
(6.3)
