Виды механических движений. Прямолинейное движение. Скорость и ускорение.

Основные понятия механики. Способы описания движения. Пространство и время .

Физика – наука, занимающаяся изучением фундаментальной структуры материи и основных форм ее движения.

Механика – наука об общих законах движения тел. Механическим движением называется перемещение тел в пространстве относительно друг друга с течением времени.

Законы механики были сформулированы великим английским ученым И.Ньютоном. Было выяснено, что законы Ньютона, как любые другие законы природы, не являются абсолютно точными. Они хорошо описывают движение больших тел, если их скорость мала по сравнению со скоростью света. Механика, основанная на законах Ньютона, называется классической механикой.

Механика включает в себя: статику, кинематику, динамику.

Статика – условия равновесия тел.

Кинематика – раздел механики, изучающий способы описания движений и связь между величинами, характеризующими эти движения.

Динамика – раздел механики, рассматривающий взаимные действия тел друг на друга.

Механическим движением называется изменение пространственного положения тела относительно других тел с течением времени.

Материальная точка – тело, обладающее массой, размером которого можно пренебречь в данной задаче.

Траектория – это воображаемая линия, по которой движется материальная точка.

Положение точки можно задать с помощью радиус-вектора: r = r(t), где t – время, за которое произошло перемещение материальной точки.

Рис.1

Тело, относительно которого рассматривается движение, называется телом отсчета.

Например, тело находится в состоянии покоя по отношению к Земле, но движется по отношению к Солнцу.

Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.

Направленный отрезок, проведенный из начального положения точки в ее конченое положение, называется вектором перемещения или просто перемещением этой точки.

Рис. 2

Δ r = r₂ – r₁

Движение точки называется равномерным, если она за любые равные промежутки времен проходит одинаковые пути.

Равномерное движение может быть как прямолинейным, так и криволинейным. Равномерное прямолинейное движение – самый простой вид движения.

Скоростью равномерного прямолинейного движения точки называют величину, равную отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло. При равномерном движении скорость постоянна.

V = Δ r/ Δt

Направлена так же, как и перемещение:

Рис.3

Графическое представление равномерного прямолинейного движения в различных координатах:

Рис.4

Уравнение равномерного прямолинейного движения точки:

r = r_о+ Vt

При проекции на ось ОХ уравнение прямолинейного движения можно записать так:

Х = Х₀ + V_х t

Путь, пройденный точкой определяется по формуле: S = Vt

Криволинейное движение.

Если траектория движения материальной точки представляет собой кривую линию, то такое движение мы будем называть криволинейным.

При таком движении изменяется как по величине, так и по направлению. Следовательно, при криволинейном движении .

Рассмотрим движение материальной точки по криволинейной траектории (рис. 2.11). Вектор скорости движения в любой точке траектории направлен по касательной к ней. Пусть в точке M₀ скорость , а в точке М – . При этом считаем, что промежуток времени Dt при переходе из точки М₀ в точку М настолько мал, что изменением ускорения по величине и направлению можно пренебречь.

Вектор изменения скорости . (В данном случае разность 2^х векторов и будет равна ). Разложим вектор , который характеризует изменение скорости как по величине, так и по направлению на две составляющие и . Составляющая , которая является касательной к траектории в точке М₀,характеризует изменение скорости по величине за время Dt, в течение которого была пройдена дуга М₀М и называется тангенциальной составляющей вектора изменения скорости ( ). Вектор , направленный в пределе, когда Dt ® 0, по радиусу к центру, характеризует изменение скорости по направлению и называется нормальной составляющей вектора изменения скорости ( ).

Таким образом, вектор изменения скорости равен сумме двух векторов .

Тогда можно записать, что

.

При бесконечном уменьшении Dt®0 угол Da при вершине DM₀АС будет стремиться к нулю. Тогда вектором можно пренебречь по сравнению с вектором , а вектор

будет выражать тангенциальное ускорение и характеризовать быстроту изменения скорости движения по величине. Следовательно, тангенциальное ускорение численно равно производной от модуля скорости по времени и направлено по касательной к траектории.

Вычислим теперь вектор , называемый нормальным ускорением. При достаточно малом Dt участок криволинейной траектории можно считать частью окружности. В этом случае радиусы кривизны M₀O и MO будут равны между собой и равны радиусу окружности R.

Повторим рисунок. ÐМ₀ОМ = ÐМСD, как углы со взаимно перпендикулярными сторонами (рис. 2. 12). При малом Dt можно считать |v₀|=|v|, поэтому DМ₀ОМ = DМDC подобны как равнобедренные треугольники с одинаковыми углами при вершине.

Поэтому из рис. 2.11 следует

Þ ,

но DS = v_ср.×Dt, тогда .

Переходя к пределу при Dt ® 0 и учитывая, что при этом v_ср. = v находим

, т.е. (2.5)

Т.к. при Dt ® 0 угол Da ® 0, то направление этого ускорения совпадает с направлением радиуса R кривизны или с направлением нормали к скорости , т.е. вектор . Поэтому это ускорение часто называют центростремительным. Оно характеризует быстроту изменения скорости движения по направлению.

Полное ускорение определяется векторной суммой тангенциального и нормального ускорений (рис. 2.13). Т.к. вектора этих ускорений взаимно перпендикулярны , то модуль полного ускорения равен ; Направление полного ускорения определяется углом j между векторами и :

Динамические характеристики

Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:

.

В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы .

• Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела является Поворот — геометрическое преобразование

5) Инерциальные системы отсчета. Преобразования Галилея.

При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта.

Различают принцип относительности Эйнштейна (который приведён выше) и принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики, подразумевая применимость преобразований Галилея, оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике.

В современной литературе принцип относительности в его применении к инерциальным системам отсчета (чаще всего при отсутствии гравитации или при пренебрежении ею) обычно выступает терминологически как лоренц-ковариантность (или лоренц-инвариантность) .

Отцом принципа относительности считается Галилео Галилей, который обратил внимание на то, что находясь в замкнутой физической системе, невозможно определить, покоится эта система или равномерно движется. Во времена Галилея люди имели дело в основном с чисто механическими явлениями. В своей книге «Диалоги о двух системах мира» Галилей сформулировал принцип относительности следующим образом:

Для предметов, захваченных равномерным движением, это последнее как бы не существует и проявляет своё действие только на вещах, не принимающих в нём участия.

Идеи Галилея нашли развитие в механике Ньютона. Однако с развитием электродинамики оказалось, что законы электромагнетизма и законы механики (в частности, механическая формулировка принципа относительности) плохо согласуются друг с другом, так как уравнения механики в известном тогда виде не менялись после преобразований Галилея, а уравнения Максвелла при применении этих преобразований к ним самим или к их решениям — меняли свой вид и, главное, давали другие предсказания (например, измененную скорость света) . Эти противоречия привели к открытию преобразований Лоренца, которые делали применимым принцип относительности к электродинамике (сохраняя инвариантной скорость света) , и к постулированию их примененимости также к механике, что затем было использовано для исправления механики с их учетом, что выразилось, в частности, в созданной Эйнштейном Специальной теории относительности. После этого обобщённый принцип относительности (подразумевающий применимость и к механике, и к электродинамике, а также к возможным новым теориям, подразумевающий также преобразования Лоренца для перехода между инерциальными системами отсчета) стал называться «принципом относительности Эйнштейна» , а его механическая формулировка — «принципом относительности Галилея» .

Виды сил в механике.

1)Силы тяготения (гравитационные силы)

В системе отсчета, связанной с Землей, на тело массой 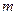действует сила ,

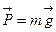называемая силой тяжести – сила, с которой тело притягивается Землей. Под действием этой силы все тела падают на Землю с одинаковым ускорением 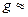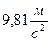, называемым ускорением свободного падения.

Весом тела называется сила, с которой тело вследствие тяготения к Земле действует на опору или подвес.

Сила тяжести действует всегда, а вес проявляется лишь тогда, когда на тело кроме силы тяжести действуют еще другие силы. Сила тяжести равна весу тела только в том случае, когда ускорение тела относительно земли равно нуля. В противном случа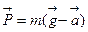е , где 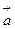- ускорение тела с опорой относительно Земли. Если тело свободно движется в поле силы тяготения, то 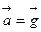и вес тела равен нулю, т.е. тело будет невесомым.

2)Сила трения скольжения возникает при скольжении данного тела по поверхности другого: ,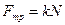

где 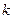- коэффициент трения скольжения, зависящий от природы и состояния трущихся поверхностей; 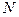- сила нормального давления, прижимающая трущиеся поверхности друг к другу. Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную движению данного тела относительно другого.

3)Сила упругости возникает в результате взаимодействия тел, сопровождающегося их деформацией. Она пропорциональна смещению частиц из положения равновесия и направлена к равновесному положению. Примером является сила упругой деформации пружины при растяжении или сжатии: ,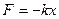

где 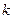- жесткость пружины; 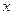- упругая деформация.

Мощность. КПд

Любая машина, которая используется для выполнения работы, характеризуется особой величиной, которая называется мощностью.

Мощность - это физическая величина, равная отношению работы ко времени, за который эта работа была выполнена. Мощность обозначается буквой N и в Системе Интернациональной измеряется в ваттах, в честь английского ученого 18-19 века Джеймса Уатта. Если мощность известна, то работу, которая выполняется за единицу времени, можно найти как произведение мощности на время. Поэтому за единицу работы можно взять работу, которая выполняется за 1 секунду при мощности 1 ватт. Такая единица работы называется ватт-секундой (Вт • с).

Если тело движется равномерно, то его мощность можно рассчитать как произведение силы тяги и скорости движения.

В реальных условиях часть механической энергии всегда теряется, поскольку идет на увеличение внутренней энергии двигателя и других частей машины. Для того чтобы характеризовать эффективность двигателей и устройств, пользуются коэффициентом полезного действия.

Коэффициент полезного действия (КПД) - это физическая величина, равная отношению полезной работы к полной работы. КПД обозначается буквой η и измеряется в процентах. Полезная работа всегда меньше полной. КПД всегда меньше 100%.

Формулировка

Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

где 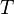— полная кинетическая энергия системы, — кинетическая энергия движения центра масс, — относительная кинетическая энергия системы^[2].

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её сферическом движении относительно центра масс.

Вывод

Приведём доказательство теоремы Кёнига для случая, когда массы тел, образующих механическую систему 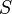, распределены непрерывно^[3].

Найдём относительную кинетическую энергию системы 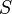, трактуя её как кинетическую энергию, вычисленную относительно подвижной системы координат. Пусть — радиус-вектор рассматриваемой точки системы 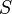в подвижной системе координат. Тогда^[4]:

где точкой обозначено скалярное произведение, а интегрирование ведётся по области пространства, занимаемой системой в текущий момент времени.

Если — радиус-вектор начала координат подвижной системы, а — радиус-вектор рассматриваемой точки системы 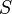в исходной системе координат, то верно соотношение:

Вычислим полную кинетическую энергию системы в случае, когда начало координат подвижной системы помещено в её центр масс. С учётом предыдущего соотношения имеем:

Учитывая, что радиус-вектор одинаков для всех , можно, раскрыв скобки, вынести за знак интеграла:

Первое слагаемое в правой части этой формулы (совпадающее с кинетической энергией материальной точки, которая помещена в начало координат подвижной системы и имеет массу, равную массе механической системы) может интерпретироваться^[2] как кинетическая энергия движения центра масс.

Второе слагаемое равно нулю, поскольку второй сомножитель в нём получается дифференцированием по времени произведения радиус-вектора центра масс на массу системы^[5], но упомянутый радиус-вектор (а с ним и всё произведение) равен нулю:

так как начало координат подвижной системы находится (по сделанному предположению) в центре масс.

Третье же слагаемое, как было уже показано, равно , т. е. относительной кинетической энергии системы .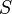

инетическую энергию материальной точки массой m, движущейся с абсолютной скоростью , определяют по формуле

где

Кинетическая энергия механической системы равна сумме кинетических энергий всех точек этой системы

Потенциальная инергия

Потенциальная энергия — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении^[1]. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[2]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными (потенциальными).

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.

Потенциальная энергия тела в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где — масса тела, — ускорение свободного падения, — высота положения центра масс тела над произвольно выбранным нулевым уровнем.

Столкновение двух тел

Закон сохранения энергии позволяет решать механические задачи в тех случаях, когда почему-либо неизвестны действующие на тело хилы. Интересным примером именно такого случая является столкновение двух тел. Этот пример особенно интересен тем, что при его анализе нельзя обойтись одним только законом сохранения энергии. Нужно привлечь еще и закон сохранения импульса (количества движения).
В обыденной жизни и в технике не так уж часто приходится иметь дело со столкновениями тел, но в физике атома и атомных частиц столкновения — очень частое явление.
Для простоты мы сначала рассмотрим столкновение двух шаров массами m₁ и m₂, из которых второй покоится, а первый движется по направлению ко второму со скоростью v₁. Будем считать, что движение происходит вдоль линии, соединяющей центры обоих шаров (рис. 205), так что при столкновении шаров имеет место так называемый центральный, или лобовой, удар. Каковы скорости обоих шаров после столкновения?
До столкновения кинетическая энергия второго шара равна нулю, а первого Сумма энергий обоих шаров составляет:

После столкновения первый шар станет двигаться с некоторой скоростью u₁. Второй шар, скорость которого была равна нулю, также получит какую-то скорость u₂. Поэтому после столкновения сумма кинетических энергий двух шаров станет равной

По закону сохранения энергии эта сумма должна быть равна энергии шаров до столкновения:

Из этого одного уравнения мы, конечно, не можем найти две неизвестные скорости: u₁ и u₂. Вот тут-то на помощь и приходит второй закон сохранения — закон сохранения импульса. До столкновения шаров импульс первого шара был равен m₁v₁, а импульс второго — нулю. Полный импульс двух шаров был равен:

После столкновения импульсы обоих шаров изменились и стали равными m₁u₁ и m₂u₂, а полный импульс стал

По закону сохранения импульса полный импульс при столкновении измениться не может. Поэтому мы должны написать:

Теперь мы имеем два уравнения:

Такую систему уравнений можно решить и найти неизвестные скорости u₁ и u₂ шаров после столкновения. Для этого перепишем ее следующим образом:

Разделив первое уравнение на второе, получим:

Решая теперь это уравнение совместно со вторым уравнением

(проделайте это самостоятельно), найдем, что первый шар после удара будет двигаться со скоростью

а второй — со скоростью

Если оба шара имеют одинаковые массы (m₁ = m₂), то u₁ = 0, а u₂ = v₁. Это значит, что первый шар, столкнувшись со вторым, передал ему свою скорость, а сам остановился (рис. 206).
Таким образом, пользуясь законами сохранения энергии и импульса, можно, зная скорости тел до столкновения, определить их скорости после столкновения.
А как обстояло дело во время самого столкновения в тот момент, когда центры шаров максимально сблизились?
Очевидно, что в это время они двигались вместе с некоторой скоростью u. При одинаковых массах тел их общая масса равна 2m. По закону сохранения импульса во время совместного движения обоих шаров их импульс должен быть равен общему импульсу до столкновения:

Отсюда следует, что

Таким образом, скорость обоих шаров при их совместном движении равна половине скорости одного из них до столкновения. Найдем кинетическую энергию обоих шаров для этого момента:

А до столкновения общая энергия обоих шаров была равна

Следовательно, в самый момент столкновения шаров кинетическая энергия уменьшилась вдвое. Куда же пропала половина кинетической энергии? Не происходит ли здесь нарушения закона сохранения энергии?
Энергия, конечно, и во время совместного движения шаров осталась прежней. Дело в том, что во время столкновения оба шара были деформированы и поэтому обладали потенциальной энергией упругого взаимодействия. Именно на величину этой потенциальной энергии и уменьшилась кинетическая энергия шаров.

Момент силы.

Основы СТО.

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями. Основным отличием СТО от классической механики является зависимость (наблюдаемых) пространственных и временных характеристик от скорости.

Центральное место в специальной теории относительности занимают преобразования Лоренца, которые позволяют преобразовывать пространственно-временные координаты событий при переходе от одной инерциальной системы отсчета к другой.

Специальная теория относительности была создана Альбертом Эйнштейном в работе 1905 года «К электродинамике движущихся тел». Несколько ранее к аналогичным выводам пришел А. Пуанкаре, который впервые назвал преобразования координат и времени между различными системами отсчёта «преобразования Лоренца».^[1]

Постулаты СТО

В первую очередь в СТО, как и в классической механике, предполагается, что пространство и время однородны, а пространство также изотропно. Если быть более точным (современный подход) инерциальные системы отсчета собственно и определяются как такие системы отсчета, в которых пространство однородно и изотропно, а время однородно. По сути существование таких систем отсчета постулируется.

Постулат 1 (принцип относительности Эйнштейна). Любое физическое явление протекает одинаково во всех инерциальных системах отсчёта. Это означает, что форма зависимости физических законов от пространственно-временных координат должна быть одинаковой во всех ИСО, то есть законы инвариантны относительно переходов между ИСО. Принцип относительности устанавливает равноправие всех ИСО.

Учитывая второй закон Ньютона (или уравнения Эйлера-Лагранжа в лагранжевой механике), можно утверждать, что если скорость некоторого тела в данной ИСО постоянна (ускорение равно нулю), то она должна быть постоянна и во всех остальных ИСО. Иногда это и принимают за определение ИСО.

Формально, принцип относительности Эйнштейна распространил классический принцип относительности (Галилея) с механических на все физические явления. Однако, если учесть, что во времена Галилея физика заключалась собственно в механике, то и классический принцип тоже можно считать распространяющимся на все физические явления. В том числе он должен распространяться и на электромагнитные явления, описываемые уравнениями Максвелла. Однако, согласно последним (и это можно считать эмпирически установленным, так как уравнения выведены из эмпирически выявленных закономерностей), скорость распространения света является определённой величиной, не зависящей от скорости источника (по крайней мере в одной системе отсчёта). Принцип относительности в таком случае говорит, что она не должна зависеть от скорости источника во всех ИСО в силу их равноправности. А значит, она должна быть постоянной во всех ИСО. В этом заключается суть второго постулата:

Постулат 2 (принцип постоянства скорости света). Скорость света в «покоящейся» системе отсчёта не зависит от скорости источника.

Принцип постоянства скорости света противоречит классической механике, а конкретно — закону сложения скоростей. При выводе последнего используется только принцип относительности Галилея и неявное допущение одинаковости времени во всех ИСО. Таким образом, из справедливости второго постулата следует, что время должно быть относительным — неодинаковым в разных ИСО. Необходимым образом отсюда следует и то, что «расстояния» также должны быть относительны. В самом деле, если свет проходит расстояние между двумя точками за некоторое время, а в другой системе — за другое время и притом с той же скоростью, то отсюда непосредственно следует, что и расстояние в этой системе должно отличаться.

Необходимо отметить, что световые сигналы, вообще говоря, не требуются при обосновании СТО. Хотя неинвариантность уравнений Максвелла относительно преобразований Галилея привела к построению СТО, последняя имеет более общий характер и применима ко всем видам взаимодействий и физических процессов. Фундаментальная константа , возникающая в преобразованиях Лоренца, имеет смысл предельной скорости движения материальных тел. Численно она совпадает со скоростью света, однако этот факт, согласно современной квантовой теории поля (уравнения которой изначально строятся как релятивистски инвариантные) связан с безмассовостью электромагнитных полей. Даже если бы фотон имел отличную от нуля массу, преобразования Лоренца от этого бы не изменились. 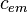Поэтому имеет смысл различать фундаментальную скорость и скорость света ^[8]. Первая константа отражает общие свойства пространства и времени, тогда как вторая связана со свойствами конкретного взаимодействия.

В связи с этим второй постулат следует формулировать как существование предельной (максимальной) скорости движения. По своей сути она должна быть одинаковой во всех ИСО, хотя бы потому, что в противном случае различные ИСО не будут равноправны, что противоречит принципу относительности. Более того, исходя из принципа «минимальности» аксиом, можно сформулировать второй постулат просто как существование некоторой скорости, одинаковой во всех ИСО, а после вывода соответствующих преобразований — показать, что это предельная скорость (потому, что подстановка в эти формулы скоростей больше этой скорости приводит к мнимости координат).

Пусть координатные оси двух инерциальных систем отсчёта 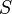и 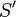параллельны друг другу, 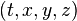— время и координаты некоторого события, наблюдаемого относительно системы 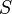, а 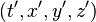— время и координаты того же события относительно системы .

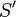Общий вид преобразований Лоренца в векторном виде^[13], когда скорость систем отсчёта имеет произвольное направление:

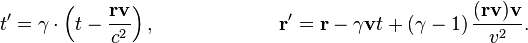
где 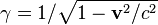— фактор Лоренца, 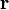и 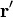— радиус-векторы события относительно систем S и S'.

Если сориентировать координатные оси по направлению относительного движения инерциальных систем (то есть в общие формулы подставить 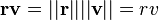) и выбрать это направление в качестве оси 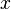(то есть так, чтобы система S' двигалась равномерно и прямолинейно со скоростью 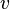относительно S вдоль оси 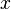), то преобразования Лоренца примут следующий вид:

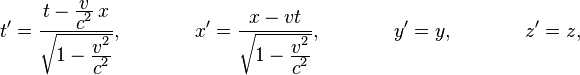
где — скорость света. При скоростях много меньше скорости света ( 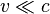) преобразования Лоренца переходят в преобразования Галилея:

Подобный предельный переход является отражением принципа соответствия, согласно которому более общая теория (СТО) имеет своим предельным случаем менее общую теорию (в данном случае — классическую механику).

Вывод преобразований Лоренца

Существует множество способов вывода преобразований Лоренца. Рассмотрим один из вариантов.

Предполагается, что начало координат системы 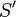(в силу однородности пространства это может быть любая покоящаяся в этой системе точка) движется относительно системы 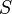со скоростью 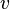. Соответственно, начало координат (покоящаяся точка) системы 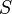движется в 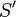со скоростью 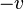. В целях упрощения дальнейшего изложения (а также самих конечных формул преобразования) будем исходить из предп