Энергия Связи и Дефект Массы Ядра

Нуклоны в ядре прочно удерживаются ядерными силами. Для того чтобы удалить нуклон из ядра, надо совершить большую работу, т. е. сообщить ядру значительную энергию.

Энергия связи атомного ядра Е_св характеризует интенсивность взаимодействия нуклонов в ядре и равна той максимальной энергии, которую необходимо затратить, чтобы разделить ядро на отдельные невзаимодействующие нуклоны без сообщения им кинетической энергии. У каждого ядра своя энергия связи. Чем больше эта энергия, тем более устойчиво атомное ядро. Точные измерения масс ядра показывают, что масса покоя ядра m_я всегда меньше суммы масс покоя, составляющих его протонов и нейтронов. Эту разность масс называют дефектом массы:

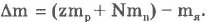
Именно эта часть массы Дт теряется при выделении энергии связи. Применяя закон взаимосвязи массы и энергии, получим:

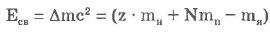
где m_н- масса атома водорода.

Такая замена удобна для проведения расчетов, и расчетная ошибка, возникающая при этом, незначительна. Если в формулу энергии связи подставить Дт в а.е.м. то для Е_св можно записать:

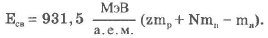
Важную информацию о свойствах ядер содержит зависимость удельной энергии связи от массового числа А.

Удельная энергия связи Е_уд - энергия связи ядра, приходящаяся на 1 нуклон:

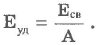
На рис. 116 приведен сглаженный график экспериментально установленной зависимости Е_уд от А.

Кривая на рисунке имеет слабо выраженный максимум. Наибольшую удельную энергию связи имеют элементы с массовыми числами от 50 до 60 (железо и близкие к нему элементы). Ядра этих элементов наиболее устойчивы.

Из графика видно, что реакция деления тяжелых ядер на ядра элементов средней части таблицы Д. Менделеева, а также реакции синтеза легких ядер (водород, гелий) в более тяжелые - энергетически выгодные реакции, так как они сопровождаются образованием более устойчивых ядер (с большими Е_уд) и, следовательно, протекают с выделением энергии (Е > 0).

Ядерные силы. Модели ядра.

ЯДЕРНЫЕ СИЛЫ- силы взаимодействия между нуклонами; обеспечивают большую величину энергии связи ядер по сравнению с др. системами. Я. с. являются наиб. важным и распространённым примером сильного взаимодействия (СВ). Когда-то эти понятия были синонимами и сам термин "сильное взаимодействие" был введён для подчёркивания огромной величины Я. с. по сравнению с др. известными в природе силами: эл.-магн., слабыми, гравитационными. После открытия p-,r- идр. мезонов, гиперо-нов и др. адронов термин "сильное взаимодействие" стали применять в более широком смысле - как взаимодействие адронов. В 1970-х гг. квантовая хромодинамика (КХД) утвердилась как общепризнанная микроскопич. теория СВ. Согласно этой теории, адроны являются составными частицами, состоящими из кварков и глюонов, а под СВ стали понимать взаимодействие этих фундам. частиц.

Капельная модель ядра — одна из самых ранних моделей строения атомного ядра, предложенная Нильсом Бором в 1936 году в рамках теории составного ядра^[1], развитая Яковом Френкелем и, в дальнейшем, Джоном Уилером, на основании которой Карлом Вайцзеккером была впервые получена полуэмпирическая формула для энергии связи ядра атома, названная в его честь формулой Вайцзеккера.

Согласно этой теории, атомное ядро можно представить в виде сферической равномерно заряженной капли из особой ядерной материи, которая обладает некоторыми свойствами, например несжимаемостью, насыщением ядерных сил, «испарением» нуклонов (нейтронов и протонов), напоминает жидкость. В связи с чем на такое ядро-каплю можно распространить некоторые другие свойства капли жидкости, например поверхностное натяжение, дробление капли на более мелкие (деление ядер), слияние мелких капель в одну большую (синтез ядер). Учитывая эти общие для жидкости и ядерной материи свойства, а также специфические свойства последней, вытекающие из принципа Паули и наличия электрического заряда, можно получить полуэмпирическую формулу Вайцзеккера, позволяющую вычислить энергию связи ядра, а значит и его массу, если известен его нуклонный состав (общее число нуклонов 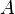(массовое число) и количество протонов 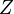в ядре):

,

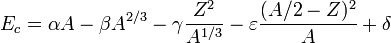где	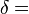{	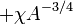для чётно-чётных ядер
0 для ядер с нечётным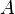
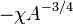для нечётно-нечётных ядер

Коэффициенты 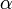, , 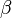, 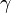и получают при статистической обработке экспериментальных данных.

Эта формула даёт довольно точные значения энергий связи и масс для очень многих ядер, что делает её достаточно универсальной и очень ценной для анализа различных свойств ядра. В целом капельная модель ядра и полуэмпирическая формула для энергии связи сыграли решающую роль в построении Бором, Френкелем и Уилером теории деления ядра^[2][3].