Дифракционная решетка как спектральный прибор. Типы дифракционных решеток.

Дифракционная решётка – важнейший спектральный прибор, предназначенный для разложения света в спектр и измерения длин волн.

Одномерная дифракционная решётка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей разделённых одинаковыми по ширине непрозрачными промежутками. Изготавливается дифракционная решётка путём нанесения на стеклянную или металлическую поверхность делительной машиной до сотен тысяч прямых равноотстоящих друг от друга одинаковых штрихов. На стеклянных решётках наблюдения можно проводить и в проходящем и в отражённом свете, на металлических – только в отражённом свете. Применяются так же и вогнутые металлические решётки, на которых штрихи наносятся на вогнутую сферическую поверхность.

Основными характеристиками любого спектрального прибора является его дисперсия и разрешающая сила (способность). Угловой дисперсией называется величина D, равная производной от угла отклонения лучей 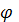по длине волны.

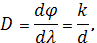где k=1,2,3,… - порядок спектра, d – постоянная решётки. Вблизи 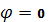дисперсия сохраняет постоянное значение; спектр с постоянной дисперсией равномерно растянут в области всех длин волн.

Разрешающая сила определяет минимальную разность длин волн 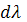, при которой все линии воспринимаются в спектре раздельно.

где k – порядок спектра, N – общее число щелей в решётке.

Разрешающая сила не зависит от постоянной d, а определяется лишь общим числом щелей и порядком спектра.

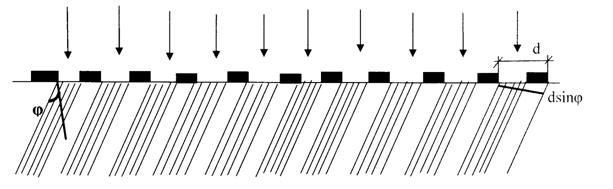
Рассмотрим простейшую идеализированную решётку, состоящую из одинаковых равноотстоящих параллельных щелей, сделанных в непрозрачном экране. Ширина щели а, ширина непрозрачной части экрана между двумя соседними щелями – b. В решётке будет осуществляться многолучевая интерференция когерентных дифрагированных пучков света, исходящих из щелей решётки при её освещении. Пусть на решётку нормально к её поверхности падает плоская монохроматическая волна.

36.

37.

Рис.27

Разность хода между вторичными волнами, исходящими из соседних щелей решётки будет 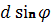, разность фаз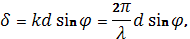

где 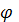- угол дифракции, k – волновое число, d – период решётки.

Пусть - поле в т. Наблюдения, излучаемое первой щелью.

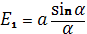
Поля, излучаемые остальными щелями:

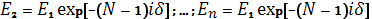
где N – общее число щелей.

Полное поле, излучаемое всеми щелями

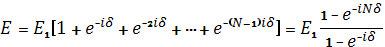
Отсюда имеем:

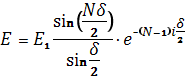
И, следовательно, амплитуда

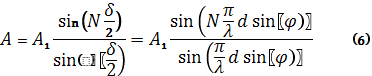
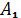- вещественная амплитуда волны от одной щели.

Для интенсивности имеем:

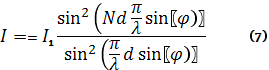
(6) и (7) - основные формулы в теории дифракционной решётки.

Проанализируем:

При 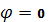разность фаз 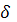тоже 0. В этом случае (6) и (7) имеют неопределённость 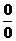. Раскрывая эти неопределённости, получим:

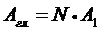
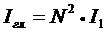(8)

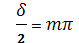(8) определяют положение центрального максимума.

При имеем тот же результат, как и (8).

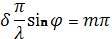
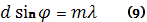, где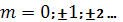

(9) – условие максимума при нормальном падении лучей на дифракционную решётку.

В направления, определяемых условием (9), получаются максимумы, интенсивность которых в 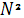раз превосходит интенсивность волны от одной щели в том же направлении. Они называются главными максимумами.

m – порядок главного максимума или порядок спектра.

Условие (9) определяет направления, в которых излучения от всех щелей решётки приходят в т. Наблюдения в одинаковых фазах, а поэтому усиливают друг друга. В таких направлениях при отдельных значениях m могут и не возникнуть максимумы. Это будет, когда 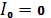, т.е. в направлениях на дифракционные минимумы от одной щели. Например, если a=b все главные максимумы чётного порядка не появятся. Условие появления главного максимума порядка 2n имеет вид: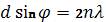

При d=2a, оно переходит в 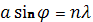, условие дифракционного минимума на щели. Следовательно, в этом направлении ни одна щель и решётка в целом не излучают.

Выражение (6) и (7) обращаются в ноль , если

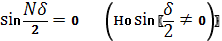
Это возможно при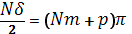

или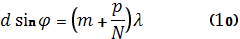

(p=1;2;3;…;N-1)

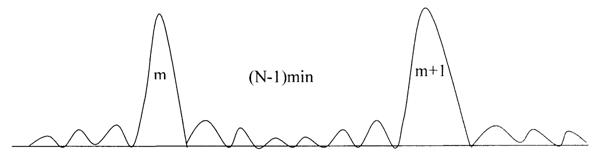В направлениях, удовлетворяющих условию (10), получаются дифракционные минимумы. Между двумя соседними минимумами получается максимум.

Такие максимумы называются добавочными. Между двумя соседними максимумами располагается (N-1) минимумов и (N-2)добавочных максимумов.

Величину 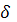– разности фаз, определяющую направление на какой-либо добавочный max, можно вычислить по формуле: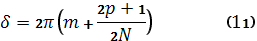

Причём интенсивность этих добавочных максимумов

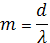
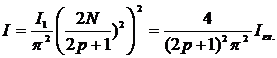(12)

Теоретически на данной дифракционной решётке можно наблюдать

главных дифракционных максимумов. Если волна падает на дифракционную решётку под углом 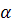, то положение главных максимумов определяется условием: 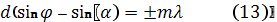Положение дифракционных минимумов при этом определяется условием:

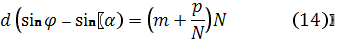
(p=1;2;3;…;N-1)

В монохроматическом свете дифракционная картина имеет вид узких и ярких главных максимумов, разделённых практически тёмным широкими промежутками.

Если дифракционная решётка освещается белым светом, то центральный максимум (максимум нулевого порядка) имеет вид белой полосы, а по обе стороны от него – дифракционные спектры 1-го, 2-го и т.д. порядков. Спектры имеют вид радужных полосок, в которых наблюдается непрерывный переход от окраски сине-фиолетового цвета у внутреннего края спектра к красной у внешнего края.

Это свойство дифракционной решётки используется для исследования спектрального состава спектра. Применяемые для этого приборы называются дифракционными спектрографами или дифракционными спектроскопами.