Трехмерный гармонический осциллятор

В общем случае потенциальная энергия выражается суммой

Уравнение Шредингера допускает разделение переменных. Если решение искать в виде ψ(x,y,z)=X(x)Y(y)Z(z), получается три дифференциальных уравнения, совпадающих по виду с одномерным. Для изотропного случая (k_x =k_y =k_z = k) значения энергии таковы

где квантовые числа n₁, n₂ и n₃ пробегают значения от 0 до бесконечности. Как и в одномерной задаче, налицо дискретность значений энергии, не равная нулю нулевая энергия. Но в трехмерном случае решение определяется тремя квантовыми числами. И особенность: одно и то же значение энергии могут иметь различные состояния, для которых выполнено условиеn₁+n₂+n₃ = const. Такие состояния называют вырожденными.

В

Вопрос 19. Атом водорода — атом, ядром которого является протон, а электронная оболочка состоит из единственного электрона. Соответствует химическому элементу водород. В общем случае, атом водорода описывается двухчастичной матрицей плотности или двухчастичной волновой функцией. Часто в квантовой механике рассматривается как электрон в электростатическом поле атомного ядра. В этом случае, электрон описывается редуцированной одночастичной матрицей плотности или волновой функцией. Из-за своей простоты как проблема двух тел атом водорода имеет специальное значение в квантовой механике и релятивистской квантовой механике поскольку соответствующие уравнения допускают точное или приближенное аналитическое решения.

В 1913 Нильс Бор получил спектральные частоты водородного атома в его модели атома водорода, имеющей множество предположений и упрощений. Эти предположения не были полностью правильны, но действительно приводили к правильным значениям энергии. Результаты расчёта Бора для частот и основных значений энергии были подтверждены в 1925/26 полным квантовым-механическим анализом, который использовал уравнение Шрёдингера. Решение уравнения Шрёдингера для электрона в электростатическом поле атомного ядра может быть найдено в аналитической форме. Из него получают уровни энергии электрона и, таким образом, его частоты. Решение уравнения Шрёдингера даёт больше информации и о формеатомных орбиталей (их анизотропии) атома водорода.

Уравнение Шрёдингера также применяется к более сложным атомам и молекулам, однако, в большинстве таких случаев, решение не является аналитическим, и необходимы компьютерные вычисления, или должны быть сделаны какие-нибудь упрощающие предположения.

Атомная орбиталь — одноэлектронная волновая функция в сферически симметричном электрическом поле атомного ядра, задающаяся главным n, орбитальным l и магнитным mквантовыми числами.

Квантовое число в квантовой механике — численное значение какой-либо квантованной переменной микроскопического объекта (элементарной частицы, ядра, атома и т. д.), характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы. Подчеркнём, что свойство тождественности выполняется не просто для частиц одного сорта, а для частиц одного сорта с одинаковыми квантовыми числами!

Некоторые квантовые числа связаны с движением в пространстве и характеризуют пространственное распределение волновой функции частицы. Это, например, радиальное (главное) (nr), орбитальное (l) и магнитное (m) квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента и его проекция на заданную ось, соответственно.

Некоторые другие квантовые числа никак не связаны с перемещением в обычном пространстве, а отражают «внутреннее» состояние частицы. К таким квантовым числам относится спин и его проекция. В ядерной физике вводится также изоспин, а в физике элементарных частиц появляется цвет, странность, гиперзаряд, очарование, прелесть и истинность.

Главное(орбитальное, радиальное) квантовое число — целое число, обозначающее номер энергетического уровня. Характеризует энергию электронов, занимающих данный энергетический уровень. С возрастающим главным квантовым числом возрастают радиус орбиты и энергия электрона. Главное квантовое число обозначается как n.

Наибольшее число электронов на энергетическом уровне, с учетом спина электрона определяется по формуле ~N=2n^2

* Орбитальное квантовое число (азимутальное) - определяет азимутальное распределение плотность вероятности локализации электрона в атоме, то есть форму электронного облака.

Связано с n -главным (радиальным) квантовым числом соотношением:

~ l= { 0;1;2;...;n-1 }
Магни?тное ква?нтовое число? — параметр, который вводится при решении уравнения Шрёдингера для электрона в водородоподобном атоме (и вообще для любого движения заряженной частицы). Его обозначают m, оно принимает целые значения: ?l, ?l+1, …, ?1, 0, 1, …, +l, где l — орбитальное квантовое число. Магнитное квантовое число характеризует ориентацию в пространстве орбитального момента количества движения электрона или пространственное расположение электронной орбитали. Каждое из 2l+1 возможных значений магнитного квантового числа определяет проекцию вектора орбитального момента на данное направление (обычно ось z). Проекция орбитального момента импульса на ось z равна L_z = m\hbar. Поскольку с орбитальным моментом связан магнитный момент, магнитное квантовое число, в частности, определяет проекцию орбитального магнитного момента водородоподобного атома на направление магнитного поля и служит причиной расщепления спектральных линий атома в магнитном поле (см. Эффект Зеемана).

Иногда магнитное квантовое число определяют для проекции любого момента частицы (орбитального L, спинового S, суммарного J=L+S). В этом случае оно принимает соответственно 2L+1, 2S+1, 2J+1 значений. Для проекций спинового и суммарного моментов магнитное квантовое число может быть полуцелым.

Вопрос 20. А́томное ядро́ — центральная часть атома, в которой сосредоточена основная его масса (более 99,9 %). Ядро заряжено положительно, заряд ядра определяет химический элемент, к которому относится атом. Размеры ядер различных атомов составляют несколько фемтометров, что в более чем в 10 тысяч раз меньше размеров самого атома. Атомное ядро состоит из нуклонов — положительно заряженных протонов и нейтральных нейтронов, которые связаны между собой при помощи сильного взаимодействия. Протон и нейтрон обладают собственным моментом количества движения (спином), равным ^{[сн 1]} и связанным с ниммагнитным моментом. Атомное ядро, рассматриваемое как класс частиц с определённым числом протонов и нейтронов, принято называть нуклидом.

Количество протонов в ядре называется его зарядовым числом 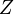— это число равно порядковому номеру элемента, к которому относится атом втаблице Менделеева. Количество протонов в ядре определяет структуру электронной оболочки нейтрального атома и, таким образом, химические свойства соответствующего элемента. Количество нейтронов в ядре называется его изотопическим числом . Ядра с одинаковым числом протонов и разным числом нейтронов называются изотопами. Ядра с одинаковым числом нейтронов, но разным числом протонов — называются изотонами. Термины изотоп и изотон используются также применительно к атомам, содержащим указанные ядра, а также для характеристики нехимических разновидностей одного химического элемента. 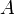Полное количество нуклонов в ядре называется его массовым числом ( ) и приблизительно равно средней массе атома, указанной в таблице Менделеева. Нуклиды с одинаковым массовым числом, но разным протон-нейтронным составом принято называть изобарами.