Принцип причинности в квантовой

Механике

Из соотношения неопределенностей часто делают вывод о неприменимости принципа причинности к явлениям, происходящим в микромире. При этом основываются на следующих соображениях. В классической механике, согласно приношу причинности — принципу классического детерминизма, по известному состоянию системы в некоторый момент времени (полностью определяется значениями координат и импульсов всех частиц системы) и силам, приложенным к ней, можно абсолютно точно задать ее состояние в любой последующий момент. Следовательно, классическая физика основывается на следующем понимании причинности: состояние механической системы в начальный момент времени с известным законом взаимодействия частиц есть причина, а ее состояние в последующий момент — следствие.

С другой стороны, микрообъекты не могут иметь одновременно и определенную координату, и определенную соответствующую проекцию импульса (задаются соотношением неопределенностей (215.1)), поэтому и делается вывод о том, что в начальный момент времени состояние системы точно не определяется. Если же состояние системы не определено в начальный момент времени, то не могут быть предсказаны и последующие состояния, т. е. нарушается принцип причинности.

Однако никакого нарушения принципа причинности применительно к микрообъектам не наблюдается, поскольку в квантовой механике понятие состояния микрообъекта приобретает совершенно иной смысл, чем в классической механике. В квантовой механике состояние микрообъекта полностью определяется волновой функцией Y(x, у, z, t),квадрат модуля которой

|Y (x, у, z, t)|²задает плотность вероятности нахождения частицы в точке с координатами х, у, z.

В свою очередь, волновая функция Y (х, у, z, t)удовлетворяет уравнению Шредингера (217.1), содержащему первую производную функции Y по времени. Это же означает, что задание функции Y₀ (для момента времени t₀) определяет ее значение в последующие моменты. Следовательно, в квантовой механике начальное состояние Y₀ есть причина, а состояние Y в последующий момент — следствие. Это и есть форма принципа причинности в квантовой механике, т. е. задание функции Y₀ предопределяет ее значения для любых последующих моментов. Таким образом, состояние системы микрочастиц, определенное в квантовой механике, однозначно вытекает из предшествующего состояния, как того требует принцип причинности.

Движение свободной частицы

Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U(x) = constи ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера (217.5) для стационарных состояний примет вид

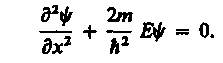(219.1)

Прямой подстановкой можно убедиться в том, что частным решением уравнения (219.1) является функция y(x) = Ae^ikx, где A = const и k = const, с собственным значением энергии

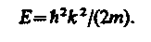(219.2)

Функция y(x) = Ae^ikx = Ae^(i/k)Ö2mEx представляет собой только координатную часть волновой функции Y(х, t). Поэтому зависящая от времени волновая функция, согласно (217.4),

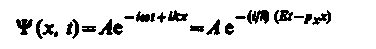(219.3)

(здесь w = E/ℏ и k = p_x/ℏ).функция (219.3) представляет собой плоскую монохроматическую волну де Бройля (см. (217.2)).

Из выражения (219.2) следует, что зависимость энергии от импульса

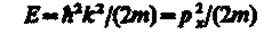
оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое число k может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным.

Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства

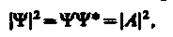
т. е. все положения свободной частицы в пространстве являются равновероятными.