Уравнение Шредингера для атома водорода. Квантовые числа и их физический смысл.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze(для атома водорода Z=1)

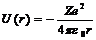где r-расстояние между электроном и ядром

Состояние электрона в атоме водорода описывается волновой функцией ψ, удовлетворяющей стационарному уравнению Шредингера, учитывающие значение U(r):

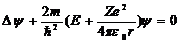
m-масса электрона, Е- полная энергия электрона в атоме.

В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции ψ_nlm­(r,θ,φ), определяемые 3 квантовыми числами: главным n,орбитальным l и магнитным m_l. Главное квантовое числоn определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения n=1,2,3….Орбитальное квантовое число l , при заданном n принимает значения l=0,1,…,(n-1) т.е. всего n значений и определяет момент импульса электрона в атоме. Магнитное квантовое число m_l, при заданном l может принимать значения m_l=0,±1,±2,…,±l, т.е. всего 2l+1 значений. Т.о. магнитное квантовое число определяет проекцию момента импульса на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентаций. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число m_l характеризует ориентацию электронного облака в пространстве.

20.Собственный механический и магнитный момент электрона. Опыт Штерна и Герлаха.

Электрон обладает собственным механическим моментом импульса L_s, называемым спином. Спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона соответствует собственный магнитный момент P_s, пропорциональный L_s и направленный в противоположную сторону: P_s=g_sL_s, g_s – гиромагнитное отношение спиновых моментов. Проекция собственного магнитного момента на направление вектора B: P_sB=±e`h/2m=±m<sub>B</sub>, где`h=h/2p, m_B=магнетон Бора. Общий магнитный момент атома p_a= векторной сумме магнитных моментов входящих в атом электрона: P_a=Sp_m+Sp_ms. Опыт Штерна и Герлаха. Проводя измерения магнитных моментов они обнаружили, что узкий пучек атомов водорода в неоднородном магнитном поле расщепляется на 2 пучка. Хотя в этом состоянии (Атомы находились в S состоянии) момент импульса электрона равен 0, а так же магнитный момент атома равен 0, поэтому магнитное поле не оказывает влияние на движение атома водорода, то есть расщепления быть не должно. Однако, дальнейшие исследования показали что спектральные линии атомов водорода обнаруживают такую структуру даже в отсутствие магнитного поля. В последствии было установлено, что такая структура спектральных линий объясняется тем, что электрон обладает собственным неуничтожимым механическим моментом, названным спином.

21.Орбитальный, спиновый и полный угловой и магнитный момент электрона.

Электрон обладает собственным моментом импульса M_S, который называется спином. Его величина определяется по общим законам квантовой механики: M_S=_{`</sub>hÖ[S(S+1)]=<sub>`}hÖ[(1/2)*(3/2)]=(1/2)_{`</sub>hÖ3, M<sub>l</sub>=<sub>`}hÖ[l(l+1)] – орбитальный момент. Проекция может принимать квантовые значения, отличающиеся друг от друга на`h. M<sub>Sz</sub>=m<sub>S`</sub>h, (m_s=±S), M_lz=m_l`h. Чтобы найти значение собственного магнитного момента умножим M_s на отношение m_s к M_s, m_s – собственный магнитный момент:

m_s=-eM_s/m_ec=-(е_`h/m_ec)Ö[S(S+1)]=-m_БÖ3, m_Б – Магнетон Бора.

Знак (-) потому что M_s и m_s направлены в разные стороны. Момент Электрона слагается из 2-х: орбитального M_l и спинового M_s. Это сложение осуществляется по тем же квантовым законам, по которым складываются орбитальные моменты разных электронов: Мj=_`hÖ[j(j+1)], j – квантовое число полного момента импульса.

22. Атом во внешнем магнитном поле. Эффект Зеемана.

Эффектом Зеемана называется расщепление энергетических уровней при действии на атомы магнитного поля. Расщепление уровней приводит к расщеплению спектральных линий на несколько компонентов. Расщепление спектральных линий при действии на излучающие атомы магнитного поля так же называется эффектом Зеемана. Зеемановское расщепление уровней обьясняется тем, что атом, обладающий магнитным моментом m_j, приобретает в магнитном поле дополнительную энергию DE=-m_jBB, m_jB- проекция магнитного момента на направление поля. m_jB=-m_Бgm_j, DE=m_Бgm_j, (m_j=0, ±1,…, ±J). Энергетический уровень расщепляется на подуровни, причем величина расщепления зависит от квантовых чисел L,S,J данного уровня.