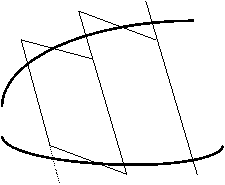
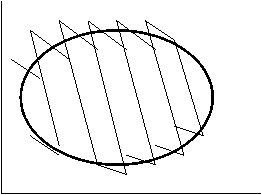
Любой цикл можно заменить бесконечно большим числом б/м циклов Карно 1-го рода.
V |
e O B Af h D O¢ C g |
Б/м цикл ABCD можно заменить б/м циклом Карно efgh, т.к. их площади отличаются на б/м величины 2-го порядка (сравним площади треугольников eOA и OBf , hO¢D и O¢Cg).
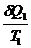 -
- 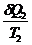 = 0 ;
= 0 ; 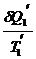 -
- 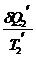 +
+ 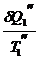 -
- 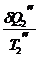 + ... = 0
+ ... = 0
В предельном случае 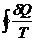 = 0
= 0
Если интеграл по замкнутому контуру равен 0, то имеется такая функция от переменных интегрирования, полный дифференциал которой равен подынтегральному выражению, т.е. имеется функция S, для которой: dS = 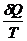
Эта функция - энтропия S.
P a · 2 1 · b V | Интеграл по замкнутому контуру можно разбить на два интеграла : 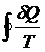 = = 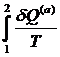 + + 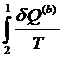 = 0 = 0 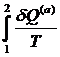 = - = - 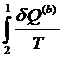 = = 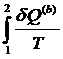 |
Т.о., сумма приведенных теплот (интеграл элементарных приведенных теплот) при переходе системы равновесным путем из состояния 1 в состояние 2 не зависит от пути процесса, а только от начального (1) и конечного (2) состояний. Следовательно, интеграл элементарных приведенных теплот в равновесном процессе равен приросту некоторой функции состояния системы :
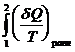 = S2 - S1 ,
= S2 - S1 , 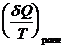 = dS
= dS
Энтропия есть функция состояния системы: ее изменение равно сумме приведенных теплот, поглощенных системой в равновесном процессе. Она является однозначной, непрерывной и конечной функцией состояния.
[S] (как и теплоемкость) : Дж/(К×моль) или Дж/(К×кг)
dQ = dA + dU / : T
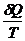 =
= 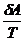 +
+ 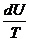 = dS
= dS
| TdS = dU + dA dU = TdS - dA dA = TdS - dU | Эти равенства охватывают уравнения I и II ЗТ ; они справедливы лишь для равновесных процессов. |
Q1 - Q2 = A ; А в необратимом цикле меньше, чем в обратимом
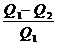 <
< 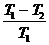
1 - 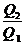 < 1 -
< 1 - 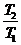 ;
; 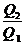 >
> 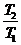 ;
; 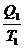 -
- 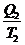 < 0
< 0
Для б/м цикла Карно 1-го вида:
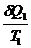 -
- 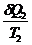 < 0 ;
< 0 ; 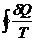 < 0- неравенство Клаузиуса
< 0- неравенство Клаузиуса
Пусть в цикле переход (а) (1 ® 2) равновесен, переход (b) (2 ® 1) - неравновесен (круговой процесс в целом - неравновесен):
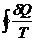 =
= 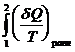 +
+ 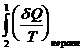 < 0
< 0
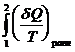 < -
< - 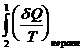 ; -
; - 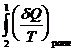 < -
< - 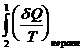
(поскольку переход (а) равновесен, пределы интегрирования можно поменять местами)
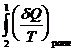 >
> 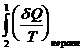 ; dS >
; dS > 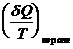
В общем случае : dS ³ 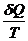
| TdS ³ dU + dA dU £ TdS - dA dA £ TdS - dU | Эти равенства охватывают уравнения I и II ЗТ ; они справедливы и для равновесных, и для неравновесных процессов. |
Если система изолированная (dQ = 0), то dS ³ 0 :
1. Равновесные процессы: dS = 0, S = const - энтропия изолированной системы постоянна, если в ней протекают равновесные процессы.
2. Неравновесные процессы: dS > 0 , S2 > S1 , S растет.
Исследуя энтропию, можно предсказать направление процесса. Если в изолированной системе для какого-либо процесса энтропия возрастает, то процесс возможен (может протекать самопроизвольно); если энтропия изолированной системы согласно расчету должна убывать, то процесс невозможен (отрицателен). При постоянстве энтропии процесс равновесен, система бесконечно близка к равновесию.
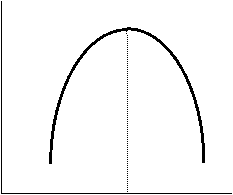 S самопро- несамопро- извольн. извольн. t равн S самопро- несамопро- извольн. извольн. t равн | В изолированной системе процессы прекратятся тогда, когда S достигнет максимального значения, возможного для данной системы при постоянстве некоторых ее параметров, а именно при постоянстве U и V (условия изолированной системы). Дальнейшее изменение состояния системы должно было бы вызвать уменьшение S, что в изолированной системе невозможно. Т.о., признаком равновесия изолированной системы является максимальное значение S при U, V = const . |
(¶S)U,V = 0, (¶ 2S)U,V < 0 - условие равновесия в изолированной системе
(¶S)U,V > 0 - условие самопроизвольного протекания процесса в изолированной системе
В системе, обменивающейся теплотой и работой с окружающей средой, возможны процессы, сопровождающиеся как возрастанием, так и убыванием S. Поэтому для решения вопроса о направлении процесса следует включить в систему все тела, участвующие в процессе, и т.о. сделать систему изолированной.
Растворы. Термодинамика многокомпонентных систем, химический потенциал. Уравнения Гиббса – Дюгема. Давление насыщенного пара бинарных жидких растворов. Закон Рауля, идеальные растворы, предельно разбавленные растворы. Отклонения от закона Рауля.
Растворами называются фазы, состав которых можно непрерывно изменять в известных пределах, то есть это фазы переменного состава. Растворы представляют собой однородные смеси молекул (атомов, ионов) двух или более веществ, между которыми имеются физические и химические взаимодействия. Растворы, как правило, термодинамически устойчивы.
Простейшие составные части раствора, которые могут быть выделены в чистом виде и смешением которых можно получить растворы любого состава - компоненты раствора.
Часто деление компонентов на растворитель и растворенное вещество условно. Обычно компонент, находящийся в избытке, называют растворителем, а остальные компоненты - растворенные вещества. Если одним из компонентов раствора является жидкость, а другими - газы или твердые вещества, то растворителем считают жидкость.
Основными параметрами состояния раствора являются р, Т и концентрации - относительные количества компонентов в растворе.


 Р
Р