Механическое движение. Классификация движений

В разделе физики «Механика» изучаются механическое движение, условия и причины, вызывающие данное движение, а также условия равновесия тел.

Механическим движением называется изменение положения тела или его частей относительно других тел с течением времени.

Всякое движение относительно. Характер движения зависит от того, относительно каких тел мы рассматриваем данное движение.

Тело, относительно которого мы рассматриваем положение других тел в пространстве, называется телом отсчета.

Системой отсчета называют систему координат, связанную с телом отсчета, и выбранный метод отсчета времени, т.е. часы. Выбор системы отсчета зависит от условий данной задачи.

Движение реальных тел, как правило, сложное. Поэтому для упрощения решения задач пользуются законом независимости движений: всякое сложное движение можно представить как сумму независимых простейших движений.

К простейшим движениям относятся поступательное и вращательное.

Поступательным называется движение, при котором отрезок, соединяющий любые две точки твердого тела, перемещается при движении параллельно самому себе. Из этого следует, что все точки тела при поступательном движении движутся одинаково, т.е. с одинаковыми скоростями, ускорениями и по одинаковым траекториям. Траектория – линия, описываемая при движении материальной точкой в пространстве.

Вращательным называется движение, при котором все точки абсолютно твердого тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, причем эти окружности лежат в плоскостях, перпендикулярных оси вращения.

Пользуясь законом независимости движений, сложное движение твердого тела можно рассматривать как сумму поступательного и вращательного движений.

На рис.1.1 показано движение карандаша. Переход из положения A₁B₁ (начальное положение) в положение A₂ B₂ (конечное) можно рассматривать как сумму двух движений: поступательного (в положение A₂B') и вращательного.

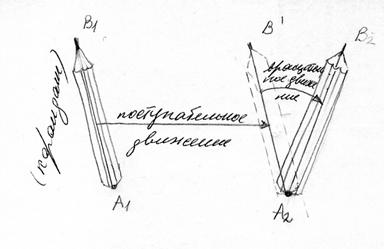
Рис. 1.1

Основная задача механики

Основной задачей механике является определение уравнения движения, то есть уравнения, позволяющего определить положение тела в любой момент времени, кроме этого определяются причины, вызывающие определенное движение.

В разделе механики – кинематика ставится задача определения уравнения движения тел без выяснения причин, вызывающих данное движение.

Для описания движения материальной точки можно использовать два способа,

Векторный способ предлагает задавать положение радиусом-вектором , проведенным из начала координат в данную точку А (рис. 1.2) .

Рис. 1.2

Координатный способ позволяет определять положение точки с помощью координат, которые при ее движении изменяются со временем, например, в декартовой системе координат положение точки задается тремя координатами

Кинематические характеристики поступательного движения твердого тела и материальной точки: перемещение, путь, скорость, ускорение (полное ускорение, тангенциальное и нормальное ускорения). Относительность движения.

Для описания движения тела необходимо ввести физические величины.

1.1Перемещение – вектор, соединяющий начальную А и конечную В точки траектории, по которой двигалась материальная точка некоторый промежуток времени Δt (рис.1.3).

Рис.1.3

1.2 Путь или длина пути l – длина траектории.

При прямолинейном движении (траектория – прямая линия) модуль перемещения равен длине пути l, если движение происходит в одном направлении.

Быстрота изменения положения материальной точки в пространстве с течением времени характеризуется средней и мгновенной скоростями.

Средняя скорость перемещения – векторная величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

= /t. (1.1)

Пусть точка движется по траектории от A до B. На рис.1.3 показаны перемещение и вектор средней скорости .

Гораздо чаще для характеристики движения мы пользуемся понятием средней скорости прохождения пути, равной отношению пути к промежутку времени, за который этот путь пройден.

v_{ср l} = l/t. (1.2)

На рис.1.4 l – это длина кривой AB. Ясно, что, поскольку ½ ½ ≤ l, то ½ ½ ≤ v_{ср l}.

Мгновенная скорость – скорость тела в данный момент времени.

Мгновенной скоростью называется предел отношения перемещения D к промежутку времени Δt, за который это перемещение произошло, при стремлении Δt к нулю, то есть первая производная радиуса-вектора по времени:

. (1.3)

Мгновенная скорость направлена по касательной к траектории. Это вытекает из следующих соображений: направлено вдоль секущей АВ (рис.1.3). Если Δt стремится к нулю, то в пределе точки А и В сольются в одну точку, при этом секущая превращается в касательную.

Рис.1.4

Рассмотрим движение точки относительно прямоугольной системы координат (рис. 1.5). Положение точки характеризуется положением радиуса –вектора . Из рисунка видно, что перемещение точки равно изменению радиуса-вектора: , .

Рис. 1.5

Тогда мгновенную скорость точки можно определить как первую производную радиуса-вектора по времени:

. (1.4)

Мгновенная скорость направлена по касательной к траектории в данной точке

Равномерным прямолинейным называется движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. При этом движении мгновенная скорость совпадает со средней скоростью перемещения:

= = = .

Пусть x₀ – координата точки в момент времени t = 0, а x – координата в момент времени t. Тогда = x - x₀.

Рис. 1.6

Из определения скорости мы можем определить уравнение движения:

Постоянный вектор определяем из начальных условий. Пусть в момент времени t= 0

Тогда уравнение движения в векторной форме имеет вид: (1.5).

В проекции на ось OX

x = x₀ + v_xt, (1.6)

Скорость v_x = ±v, где v = .

Тогда получаем закон движения в том виде, в котором чаще всего он используется при решении задач:

x = x₀ ± vt. (1.7)

Относительность движения

Для описания движения необходимо выбрать систему отсчета. В ряде задач приходится рассматривать движение одного и того же тела относительно разных тел, причем эти тела, а следовательно, связанные с ними системы отсчета, могут двигаться друг относительно друга.

Если известна скорость тела в движущейся системе отсчета со скоростью, называемой относительной скоростью , и известна скорость подвижной системы относительно неподвижной со скоростью, называемой переносной , то скорость тела относительно неподвижной системы отсчета, абсолютная скорость – , определяется согласно классическому закону сложения скоростей:

= + ,

Т.е. абсолютная скорость тела равна векторной сумме относительной и переносной скоростей.

Обратим внимание на то, что взяв производную по времени от левой и правой частей этого равенства, мы получим выражение для мгновенного ускорения.

Если же тела, с которыми связаны неподвижная и подвижная системы отсчета движутся равномерно друг относительно друга и одна из систем является инерциальной (см. ниже), то ускорения тела равны:

=

Ускорение

Величина, характеризующая быстроту изменения скорости, называется ускорением.

Среднее ускорение – величина, равная отношению изменения скорости к промежутку времени, за который это изменение произошло:

= /Δt. (1.10)

Если и – мгновенные скорости в моменты времени t₁ и t₂, то

= – , Δt = t₂ – t₁.

На рис.1.8 изображены векторы мгновенных скоростей. Чтобы их сравнить, сделаем параллельный перенос вектора в точку А. Тогда определит направление .

Рис. 1.8

Мгновенное ускорение – ускорение тела в данный момент времени. Это физическая величина, равная пределу отношения изменения скорости к промежутку времени, за который это изменение произошло, при стремлении промежутка времени к нулю:

= . (1.11)

Вектор направлен так же, как и вектор при Δt ® 0, и не совпадает в общем случае с направлением вектора скорости .

Рис. 1.9

Пусть вектор мгновенного ускорения направлен, как указано на рис.1.9, под углом к вектору скорости. Ускорение характеризует изменение скорости по модулю и по направлению. Разложим ускорение на две составляющие: а_t – тангенциальное (касательное) ускорение и а_n – нормальное (центростремительное) ускорение. Компонента а_t направлена по касательной к траектории и характеризует изменение скорости по модулю, а_n направлено к центру кривизны траектории (по нормали к скорости) и характеризует изменение скорости по направлению. Компонента а_n = v²/R, где – мгновенная скорость, R – радиус кривизны траектории в данной точке,

= + . (1.12)

Модуль мгновенного ускорения равен

а_мгн = . (1.13) При прямолинейном движении a_n = 0, скорость не изменяется по направлению. Если = остается постоянным, то материальная точка движется прямолинейно и равноускоренно. В этом случае среднее ускорение равно мгновенному:

= .

Из определения ускорения следует ,(1.14)

Направим ось ОХ вдоль направления движения тела в момент времени t = 0 (рис.1.10). Из определения ускорения следует

a_x = ,

где v_0x – скорость тела при t = 0.

Тогда v_x = v_0x + a_xt. (1.12)

На рис.1.10 показаны различные направления ускорения.

Проинтегрировав v_x (t) по времени найдем уравнение прямолинейного равноускоренного движения:

(1.15)

В векторном виде уравнение движения имеет вид:

(1.16)

Чаще при решении задач пользуемся уравнениями:

х = х₀ ± v₀t ± at²/2,

v_x = ±v₀ ± at, (1.17)

где v₀ и a – модули начальной скорости и ускорения.