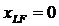Свойства треугольной диаграммы

В любом процессе экстракции можно выделить три составляющие: раст-ль; извлекаемый компонент, неизвлекаемый компонент.

Равносторонний ∆, вершины к-го характеризуют какое-либо аддитивное свойство чистых или обобщенных комп-ов (конц-ию, вязкость, индекс вязкости и т.п.), а каждая точка внутри треугольника отвечает трехкомпонентной системе.

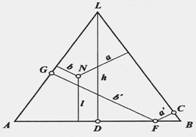
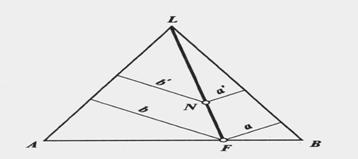
С-ма сост. из трех комп-ов А, В и L, представленных вершинами равностороннего ∆-а ABL, а точка N внутри ∆-а хар-ет смесь указанных комп-ов. Массовые доли комп-ов:

; ; ;

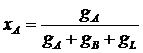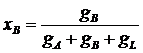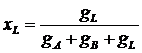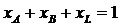
Бинарная смесь исходных компонентов характеризуется точкой, находящейся на соответствующей стороне треугольника.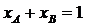

Основные свойства треугольной диаграммы:

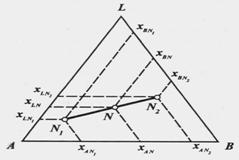
Первое. Если из двух с-м, хар-ых (∙) N₁, и N₂, путем смешения получают новую с-му, хар-ую (∙) N, то (∙) всех трех с-м лежат на одной прямой, к-ая (∙) N делится на части, обратно пропорциональные кол-вам комп-ов в исходных системах

Ур-ние соотв-ет прямой, проходящей через (∙) N₁, N и N₂, а (∙) N делит прямую N₁N₂на части, обратно пропорц. массам (или объемам) исх-ых с-м (правило рычага).

Аналогичным образом можно получить также следующие соотношения:

Второе. Если при попарном смешении неск-их с-м получается одна и та же с-ма, хар-ая (∙) N, то на ∆-ой диаграмме прямые, соединяющие (∙) попарно смешиваемых систем, пересекутся в (∙) N.

Так, если попарно смешать с-мы N₁ и N₂, N₃ и N₄, к-ые обр-ют с-му N , то прямые N₁N₂ и N₃N₄пересекутся в (∙) N. При этом справедливо следующее соотношение:

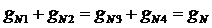
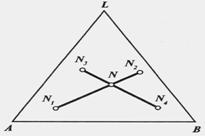
Третье. Если разность кол-в любых двух с-м есть величина пост., то на ∆-ой диаграмме прямые, проходящие через соответствующие пары (∙), хар-ие исходные с-мы, пересекутся в одной (∙) М.

Пусть имеются с-мы R₁, R₂ и R₃,к-ые при удалении из с-м S₁, S₂ и S₃ обр-ют одну и ту же с-му М.

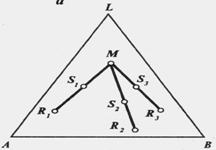
Согласно первому св-ву можно записать: ; ;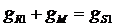

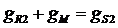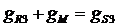
Откуда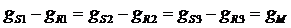

При этом (∙) S₁, S₂ и S₃делят соотв-ие прямые R₁М, R₂M и R₃M на части, обратно пропорциональные кол-вам соотв-их с-м, ; ;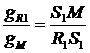

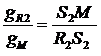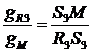
(∙) пересечения М может оказаться вне ∆-ой диаграммы

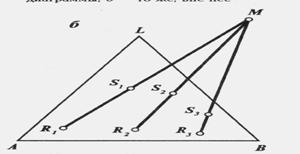
Четвертое. Любая (∙), лежащая на линии LF, характеризуется постоянством соотношений комп-ов А и В. Другими словами, все р-ры исходной смеси F, состоящей из комп-ов А и В, и комп-та L, определяются (∙)-ами, лежащими на прямой LF.

Из подобия соответствующих ∆-ов следует: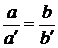

Поэтому перемещение из (∙) Fв (∙) Nможно рассматривать как добавление к р-ру Fкомп-та L в соответствующих кол-вах. В соотв-вии с 1-ым св-вом все такие р-ры будут находиться на прямой LF, при этом соотношение м/у конц-ями комп-тов А и В будет оставаться неизменным и равным соотношению этих комп-тов в исходном р-ре F.Перемещение (∙) Nв (∙) L будет отвечать бесконечному разбавлению исходной системы третьим компонентом L, т.е. 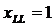,а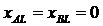

Перемещение (∙) N по линии LFвниз соответствует постепенному удалению комп-та L из р-ра. При совмещении (∙) Nс (∙) F третий комп-нт L полностью удаляется из р-ра, а смесь будет состоять только из к-тов А и В