Упражнение 1. Определение периода свободных колебаний

1. Собрать колебательный контур, взяв для этого эталонную катушку с индуктивностью L = 0,001 Гн, конденсатор емкостью С = 1,0 мкФ и потенциометр R = 30…50 Ом, чтобы наблюдать на экране осциллографа не менее 6…8 периодов свободных колебаний.

2. Подготовить к работе установку по схеме, представленной на рис.4. Конденсатор контура соединить со входом «Y» осциллографа. Подвижный контакт потенциометра поставить в верхнее положение (R = 0).

3. Включить осциллограф и на его экране добиться четкой картины затухающих колебаний, регулируя режим синхронизации, скорость развёртки и чувствительность канала. Пользуясь регулятором усиления и рукояткой смещения луча по горизонтали, установить на экране осциллографа рабочий участок осциллограммы, соответствующий свободным колебаниям.

4. Измерить частоту и период свободных колебаний.

Упражнение 2. исследование зависимости логарифмического декремента затухания от активного сопротивления.

1. При сопротивлении потенциометра R = 0 рассчитать логарифмический декремент затухания g и собственное сопротивление потерь R₀ в контуре.

Для увеличения точности вычислений g рекомендуется измерять амплитуду U_m (в единицах масштаба координатной сетки на экране) не в соседних максимумах, а, например, в первом (произвольном) и Z-м максимумах. Тогда g можно вычислить по формуле:

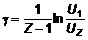, (11)

где U₁ и U_Z – соответствующие амплитуды.

Вычислив логарифмический декремент затухания и, зная период свободных колебаний в контуре Т, найти коэффициент затухания a(при сопротивлении потенциометра R = 0):

a = g/T,

а затем сопротивление потерь в контуре:

R₀ = a×2L.

2. Исследовать зависимость логарифмического декремента затухания от сопротивления и построить график этой зависимости. Сопротивление контура изменять с помощью потенциометра R через каждые 0,1…0,2 Ом. При оценке затухания к сопротивлению потенциометра R необходимо прибавлять собственное сопротивление контура R₀.

3. Изменяя сопротивление потенциометра, по осциллограмме определить критическое сопротивление R_к, при котором наступает апериодический процесс. Сравнить полученное значение R_к с теоретическим, рассчитанным по формуле (10).

Упражнение 3. Исследование зависимости периода свободных колебаний от параметров контура и проверка формулы томсона

1. Измерить период свободных колебаний для второй эталонной катушки.

2. Измерить период свободных колебаний при последовательном соединении двух эталонных катушек.

3. Рассчитать по формуле Томсона периоды свободных колебаний исследованных контуров и сравнить с экспериментальными значениями.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой ток называют квазистационарным? Записать условия квазистационарности.

2. Какие колебания называются свободными колебаниями? Какими уравнениями описываются собственные колебания?

3. От чего зависит период свободных колебаний, какова эта зависимость?

4. Какими величинами характеризуют затухающие электромагнитные колебания?

5. Что такое логарифмический декремент затухания? Как он связан с коэффициентом затухания?

6. На основании каких рассуждений получена формула (7) для определения периода свободных колебаний?

7. Как определяется на опыте сопротивление потерь в контуре? Из чего складываются потери энергии в контуре (указать не менее трех возможных механизмов потерь)?

Лабораторная работа № 11

ИЗУЧЕНИЕ МАГНИТНого гистерезиса

В ФЕРРоМАГНЕТИКе

Цель работы: исследовать явление магнитного гистерезиса, зарегистрировать кривую намагничивания ферромагнитного образца и определить потери энергии на перемагничивание.

Приборы и принадлежности: лабораторный стенд для наблюдения петли гистерезиса, двухканальный осциллограф, генератор, соединительные провода.

КРАТКАЯ ТЕОРИЯ

В общем случае вектор магнитной индукции в среде связан с напряженностью магнитного поля соотношением

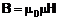, (1)

где m₀ = 4pЧ10^–7 Гн/м - магнитная постоянная; m- магнитная проницаемость среды (m = 1 для вакуума). Магнитная индукция в среде определяется индукцией в вакууме и намагниченностью среды:

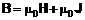, (2)

где J - вектор намагничивания, равный магнитному моменту единицы объема магнетика. Так как вектор J связан с вектором напряжённости магнитного поля соотношением:

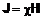, (3)

где c - магнитная восприимчивость среды, перепишем (2):

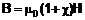. (4)

Из сравнения (1) и (4) следует, что

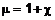. (5)

Магнитная восприимчивость и магнитная проницаемость характеризуют магнитные свойства вещества.

В зависимости от знака и величины восприимчивости c при нормальных условиях все вещества можно подразделить на три группы: диамагнетики, парамагнетики и ферромагнетики.

Парамагнетики характеризуются положительной восприимчивостью (c > 0), величина которой может принимать значения в интервале от 10^–5 до 10^–3. Во внешнем магнитном поле намагниченность парамагнетиков совпадает по направлению с внешним полем (J­­H).

Диамагнетики имеют отрицательное значение магнитной восприимчивости (c < 0) и имеют порядок величины 10^–6. Во внешнем магнитном поле намагниченность диамагнетиков противоположна направлению внешнего поля (J­¯H).

Рис. 1. Зависимость намагниченности от напряженности внешнего магнитного поля для пара- и диарамагнетиков.

Диа- и парамагнетики принадлежат к классу слабомагнитных веществ, их магнитная проницаемость близка к единице (абсолютное значение c очень мало).

В соответствии с формулой (3) существует линейная зависимость между J и H, как показано на рис. 1.

Вещества, в которых вектор намагничивания может значительно превышать по величине индукцию внешнего поля, называются ферромагнетиками.

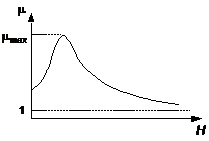Рис. 2. Зависимость магнитная проницаемости ферромагнетика от напряжённости магнитного поля

Ферромагнетики могут обладать спонтанной намагниченностью, то есть они намагничены при отсутствии поля. Магнитная восприимчивость c ферромагнетиков имеет высокое значение и может достигать величины 10³…10⁵. Магнитная проницаемость ферромагнетика является нелинейной функцией от напряжённости магнитного поля (рис. 2).

Рис.3. Петля гистерезиса.

Если ненамагниченный ферромагнетик поместить в пространство с постоянно увеличивающимся магнитным полем, то зависимость индукции магнитного поля внутри ферромагнетика B от напряжённости внешнего магнитного поля Н (рис.3) выразится участком 0-1 (начальная кривая намагничивания), вид которого определяется свойствами исследуемого магнетика.

Если продолжать увеличивать внешнее магнитное поле, то кривая намагничивания перейдёт в линейный участок, поскольку в результате насыщения величина намагниченности J станет постоянной, и B будет возрастать только за счёт увеличения H (см. выражение (2)).

При уменьшении напряжённости внешнего поля до нуля намагничивание будет изменяться в соответствии с кривой 1-2. Величина В_n, соответствующая отрезку 0-2 называется остаточной индукцией и является характеристикой ферромагнетика.

Остаточной индукции соответствует остаточная намагниченность J_n. Именно с наличием остаточной намагниченности связано существование постоянных магнитов. Остаточная намагниченность исчезает при температурах выше точки Кюри.

Остаточную индукцию можно устранить, если приложить к образцу обратное поле с напряжённостью –Н_c. Величина Н_c называется коэрцитивной силой и тоже является характеристикой ферромагнетика. При дальнейшем увеличении обратного намагничивающего поля вновь достигается насыщение. Если от точки насыщения 3 уменьшать магнитное поле до нуля, а затем, изменив направление, увеличивать поле, получим кривую намагничивания 3-4-1. Замкнутая кривая «1-2-3-4-1» называется петлёй гистерезиса.

Размеры петли гистерезиса увеличиваются с ростом амплитуды изменения напряжённости поля Н, но только до определённого предела (Н_m). Максимально возможная площадь петли соответствует случаю насыщения. Очевидно, что максимальное значение коэрцитивной силы Н_с и остаточной индукции В_n можно получить только по максимальной петле гистерезиса.

ПРАКТИЧЕСКАЯ ЧАСТЬ