Столкновения тел. неупругое и абсолютно упругое столкновение

При соударении тел кинетическая энергия, которой они обладали перед ударом, частично или полностью переходит в энергию упругой деформации и во внутреннюю энергию этих тел.

Существуют два предельных случая удара: абсолютно упругий и абсолютно неупругий. Абсолютно упругим называется удар, при котором механическая энергия тел не переходит в другие виды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга, и потенциальная энергия снова переходит в кинетическую, и тела разлетаются со скоростями, определяемыми по законам сохранения энергии и импульса.

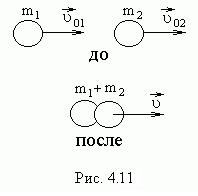
Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает. Кинетическая энергия тел полностью или частично переходит во внутреннюю энергию. После удара столкнувшиеся тела либо движутся вместе, либо покоятся. При таком ударе выполняется закон сохранения импульса, закон же сохранения механической энергии не выполняется.

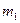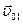Рассмотрим абсолютно неупругий удар двух частиц (материальных точек), образующих замкнутую систему (рис. 4.11). Массы частиц и , их скорости до удара и 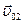. После удара скорости частиц одинаковы и равны 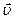. По закону сохранения импульса имеем:

.

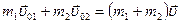Тогда скорость частиц после удара .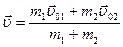

Теперь рассмотрим абсолютно упругий удар, ограничившись рассмотрением центрального удара двух однородных шаров. Удар называется центральным, если до удара шары движутся вдоль прямой, проходящей через их центры. При центральном ударе соударение может произойти, если шары движутся навстречу друг другу (рис. 4.12), либо один из шаров догоняет другой (рис.4.13).

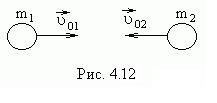
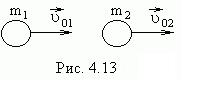
Будем предполагать, что шары образуют замкнутую систему и вращение шаров отсутствует.

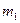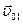Массы шаров и , их скорости до удара и 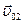. После удара их скорост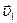и и 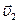. По закону сохранения энергии

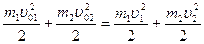, (4.15)

по закону сохранения импульса 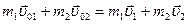. (4.16)

Умножив уравнение (4.15) на 2 и сгруппировав, получаем: 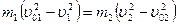, или 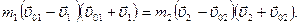Из (4.16)

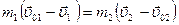. (4.17)

Разделим первое из этих уравнений на второе

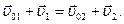(4.18)

Умножим (4.18) на и вычтем результат из (4.17)

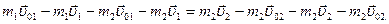
Получаем

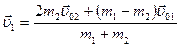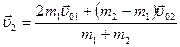, . (4.19)

Из выражений (4.19) видно, что после удара скорости шаров не могут быть одинаковыми. Действительно, если приравнять 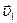и 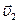, получаем 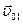= 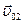, т.е. скорости шаров должны быть одинаковыми и до удара, но в этом случае соударение не может произойти.

Рассмотрим случай, когда массы соударяющихся шаров равны 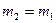. При этом, как следует из (4.19) 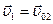и 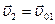, т.е. шары при столкновении обмениваются скоростями.

При рассмотрении абсолютно упругого удара шара о неподвижную или движущуюся стенку последнюю следует рассматривать как шар бесконечно большой массы. Тогда разделив числитель и знаменатель выражения (4.19) на (массу стенки) и считая 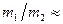0, получим .

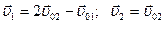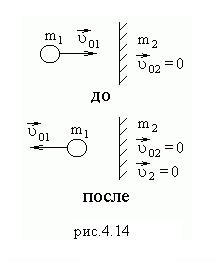
Если стенка неподвижная (рис.4.14), 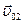=0, скорость шара меняет свое направление на противоположное, модуль скорости остается неизменным.