Закон сохранения полной механической энергии в поле консервативных сил
Сведем вместе результаты, полученные в предыдущих параграфах. Рассмотрим систему, состоящую из 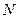 частиц с массами
частиц с массами 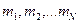 . Частицы взаимодействуют друг с другом силами
. Частицы взаимодействуют друг с другом силами 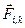 , модули которых зависят только от расстояния
, модули которых зависят только от расстояния 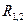 между частицами. Ранее было установлено, что такие силы являются консервативными, и работа, совершаемая этими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть, кроме внутренних сил, на
между частицами. Ранее было установлено, что такие силы являются консервативными, и работа, совершаемая этими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть, кроме внутренних сил, на 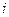 -ю частицу действует внешняя консервативная сила
-ю частицу действует внешняя консервативная сила 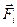 и внешняя неконсервативная сила
и внешняя неконсервативная сила 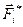 . Уравнение движения для
. Уравнение движения для 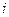 -той частицы имеет вид
-той частицы имеет вид
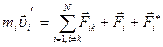 .
.
Умножив это уравнение на 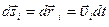 и сложив вместе все
и сложив вместе все 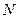 уравнений, получаем:
уравнений, получаем:
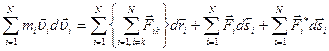
Левая часть этого выражения представляет собой приращение кинетической энергии системы: 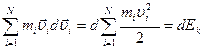 . Первое слагаемое правой части равно убыли потенциальной энергии взаимодействия, как
. Первое слагаемое правой части равно убыли потенциальной энергии взаимодействия, как
следует из выражения (4.14): 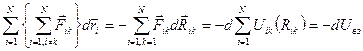 .
.
Второе слагаемое равно убыли потенциальной энергии системы во внешнем поле консервативных сил: 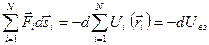 . Последнее слагаемое представляет собой работу внешних неконсервативных сил
. Последнее слагаемое представляет собой работу внешних неконсервативных сил 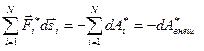 . Окончательно получаем:
. Окончательно получаем: 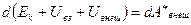 .
.
Величина 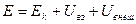 есть полная механическая энергия системы. Если на систему не действуют внешние неконсервативные силы, то полная механическая энергия сохраняется. Это закон сохранения механической энергии.
есть полная механическая энергия системы. Если на систему не действуют внешние неконсервативные силы, то полная механическая энергия сохраняется. Это закон сохранения механической энергии.
Для замкнутой механической системы этот закон формулируется следующим образом: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной.
Если в замкнутой системе, кроме консервативных, действуют неконсервативные силы, то полная механическая энергия не сохраняется, и ее изменение равно работе неконсервативных сил: 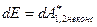
Проинтегрировав, получаем: 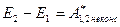 .
.
В этом случае механическая энергия переходит в другие виды энергии, и выполняется более общий закон сохранения всех видов энергии.
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Мы рассмотрели энергию, которая представляет собой аддитивный интеграл движения, сохраняющийся в замкнутой системе. Другим таким интегралом движения является импульс механической системы. Рассмотрим систему, состоящую из n материальных точек, в которой на 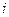 -ю материальную точку действуют внутренние силы
-ю материальную точку действуют внутренние силы 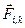
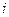 и внешние силы, равнодействующая которых
и внешние силы, равнодействующая которых 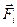 . Запишем уравнения динамики для всех частиц системы:
. Запишем уравнения динамики для всех частиц системы:
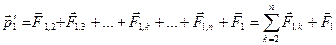 ,
,
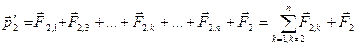 ,
,
………………………………………………………….
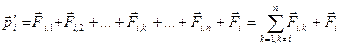 ,
,
…………………………………………………………..
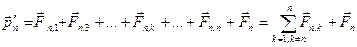 .
.
Сложив эти уравнения и приняв во внимание, что внутренние силы попарно равны, получаем:
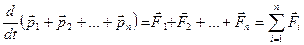 .
.
Под знаком дифференциала стоит полный импульс системы. Тогда можно записать: 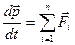 .
.
При отсутствии внешних сил 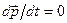 , следовательно, для замкнутой системы полный импульс сохраняется.
, следовательно, для замкнутой системы полный импульс сохраняется.
Следует отметить, что полный импульс остается постоянным и для незамкнутой системы, когда векторная сумма внешних сил равна нулю. Если эта сумма не равна нулю, однако ее проекция на некоторое направление есть ноль, то сохраняется составляющая импульса на это направление.
