Энергия. работа и кинетическая энергия. теорема кенига

Энергия является количественной мерой различных форм движения материи и соответствующих им взаимодействий. Движение – неотъемлемое свойство материи. Поэтому любое тело, любая система тел и полей обладают энергией. Энергия характеризует возможные изменения движения системы. Эти изменения происходят вследствие взаимодействия между частями системы, а также между системой и внешней средой. Для различных форм движения и соответствующих им взаимодействий в физике вводят различные виды энергии – механическую, внутреннюю, электрическую и т.д. В механике различают два вида механической энергии: кинетическую и потенциальную.

Кинетической энергией механической системы называется энергия механического движения этой системы.

Изменение механического движения системы происходит только под действием приложенной к ней силы. Поэтому для отыскания вида функции кинетической энергии воспользуемся вторым законом Ньютона.

Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки). Уравнение движения частицы 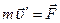умножим на перемещение 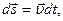получаем

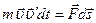. (4.1)

Здесь 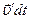- приращение скорости частицы 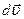за время 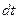. Левую часть выражения (4.1) приведем к виду:

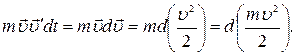(4.2)

Тогда имеем: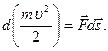

Если система замкнута, то 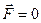, и 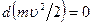, а сама величина

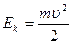(4.3)

остается постоянной. Эта величина и называется кинетической энергией. В случае изолированной частицы кинетическая энергия сохраняется и является интегралом движения.

Умножив на массу частицы 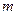числитель и знаменатель выражения (4.3) и воспользовавшись определением импульса, получаем: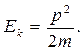

Кинетическая энергия механической системы, состоящей из 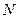частиц, равна сумме кинетических энергий отдельных частиц:

.

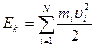Если на частицу действует сила 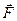, кинетическая энергия не остается постоянной. Согласно (4.2), приращение кинетической энергии частицы за время 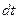в этом случае равно скалярному произведению 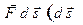- перемещение частицы за время 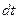). Величина 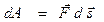называется работой, совершаемой силой 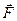на пути 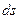, где 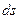- модуль перемещения .

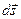Проинтегрировав выражение (4.2) вдоль траектории от точки 1 до точки 2, получаем:

.

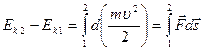Величина 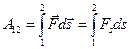(4.4)

есть работа силы 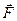на пути 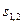. Таким образом, работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии этой частицы:

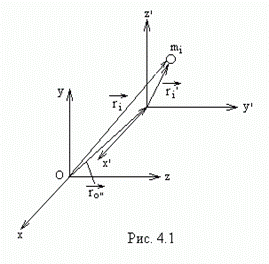
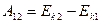. (4.5)

Формула (4.3) для кинетической энергии частицы справедлива как в инерциальной, так и в неинерциальной системе отсчета. При переходе из одной системы отсчета в другую, движущуюся относительно первой с некоторой скоростью 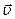, скорость частицы меняется, следовательно, меняется и кинетическая энергия.

Рассмотрим две системы отсчета: инерциальную 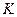и систему отсчета 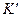, движущуюся относительно 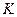поступательно со скоростью 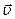. Скорость 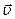может быть как постоянной (тогда система 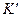инерциальная), так и зависящей от времени ( в этом случае система 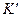неинерциальная). Из рисунка 4.1 видно, что радиус-векторы 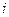-той материальной точки в системах отсчета 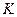и 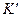связаны соотношением:

,

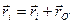где 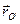- радиус-вектор в системе 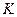точки 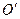(начала отсчета координат в системе 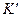). Продифференцировав это выражение по времени, получаем для скоростей:

.

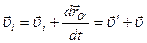Возведем это равенство в квадрат: .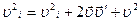

Подставим значение 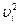в формулу кинетической энергии механической системы, получаем кинетическую энергию относительно системы :

,

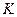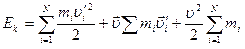или 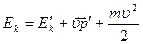. Здесь 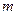- масса всей системы, 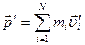- импульс механической системы в 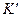, 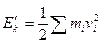- кинетическая энергия системы в .

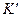Очевидно, 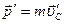, где 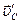- скорость центра масс системы в 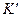. Поэтому, если в качестве 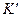взять систему центра масс механической системы, то 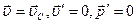и

.

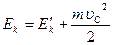Это теорема Кенига: кинетическая энергия механической системы равна сумме кинетической энергии той же системы в ее движении относительно центра масс и кинетической энергии, которую имела бы рассматриваемая система, двигаясь поступательно со скоростью центра масс.

Выражение (4.4) можно представить в ви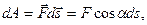де: где 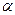- угол между направлениями силы и перемещения. Если этот угол острый ( 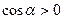), работа положительна, если 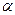- тупой ( 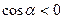), работа отрицательна. При 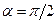работа равна нулю.

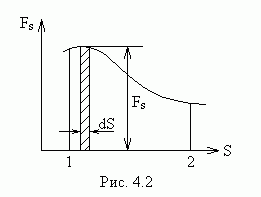
На рис.4.2 представлен график проекции силы на направление перемещения 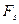как функции положения частицы на траектории. Из рисунка видно, что элементарная работа 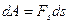численно равна площади заштрихованной полоски, а работа 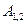на пути 1-2 численно равна площади фигуры, ограниченной кривой 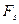, вертикальными прямыми 1 и 2 и осью S.

Пусть на тело действует одновременно несколько сил 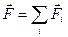. Из дистрибутивности скалярного произведения векторов вытекает, что работа 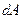, совершаемая результирующей силой на пути 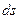, может быть представлена в виде:

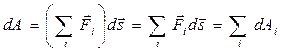
- работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой силой в отдельности.

Очевидно, элементарное перемещение 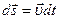, поэтому выражение для элементарной работы (4.4) принимает вид:

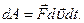
Тогда работа, совершаемая за промежуток времени от 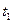до 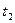, будет равна

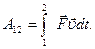
Работа, совершаемая в единицу времени, называется мощностью: .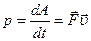

Проинтегрировав выражение (4.2) вдоль траектории от точки 1 до точки 2, получаем: 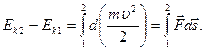Величина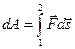

есть работа силы 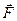на пути 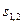. Таким образом, работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии этой частицы: