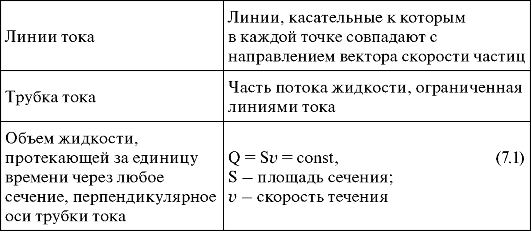
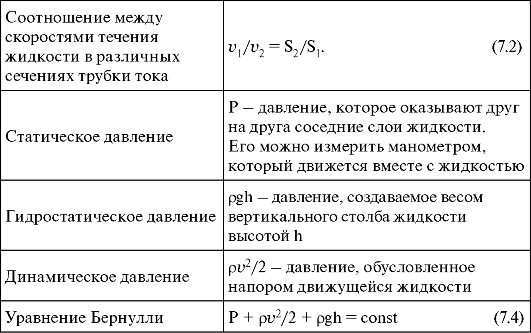
Горизонтальная трубка тока переменного сечения

При этом h₁ = h₂ и уравнение (7.3.) принимает вид

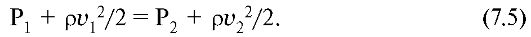Отсюда следует, что статическое давление идеальной жидкости при течении по горизонтальной трубке возрастает там, где скорость ее уменьшается, и наоборот. Это можно продемонстрировать с помощью манометрических трубок, уровень поднятия жидкости в которых пропорционален статическому давлению (рис. 7.3). Видно, что в широком сечении (а), где скорость течения меньше, статическое давление больше, чем в узком сечении (б).

Наклонная трубка тока постоянного сечения

В такой трубке скорость жидкости везде одинакова (v = const), и уравнение (7.3) принимает вид

Следовательно, скорость истечения струи равна скорости тела при свободном падении с высоты h. Соотношение (7.9) - это формула Торричелли.

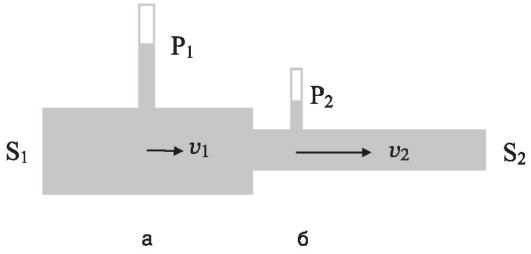Рис. 7.3.Горизонтальная трубка переменного сечения

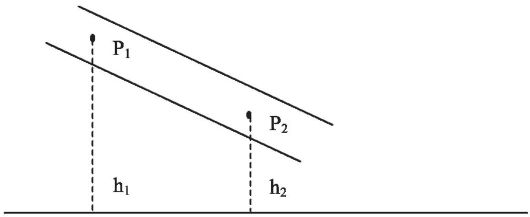Рис. 7.4.Наклонная труба постоянного сечения

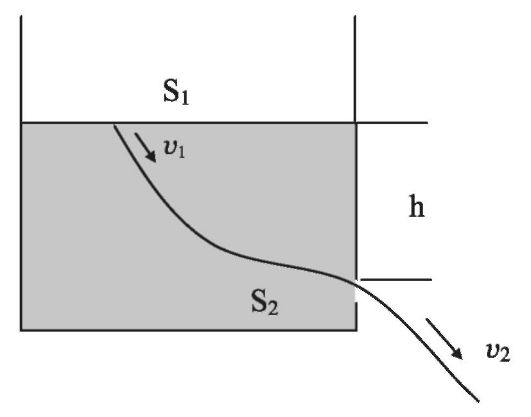Рис. 7.5.Линия тока при истечении жидкости из небольшого отверстия широкого сосуда

Измерение скорости жидкости

Установим в разных местах горизонтальной цилиндрической трубы (струи жидкости) одного сечения две трубки: 1) манометрическую трубку, плоскость отверстия которой расположена параллельно движению жидкости; 2) трубку, изогнутую под прямым углом навстречу движению жидкости (трубку Пито) (рис. 7.6).

В движущемся потоке жидкость в трубках поднимается на разную высоту. Давление под манометрической трубкой равно статическому давлению Р. Оно уравновешивается давлением атмосферы Р_а и давлением столба жидкости h₂:

Имея систему двух таких трубок, вычисляют скорость потока жидкости по формуле (7.10).

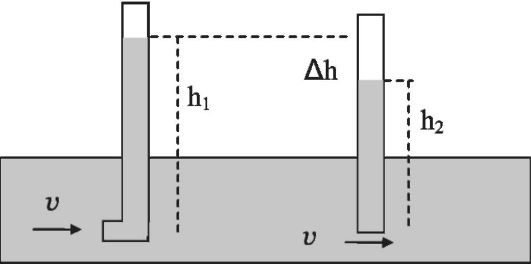Рис. 7.6.Измерение скорости жидкости

Принцип работы инжектора, ингалятора

В медицине широкое применение находят приборы, действие которых основано на использовании законов гидродинамики. Рассмотрим два таких прибора.

Инжектор

Этот прибор используют для дозированной подачи пациенту газообразного препарата. Например, закиси азота или кислорода. Препарат из баллона поступает в смесительную камеру через узкое сопло (рис. 7.7).

При этом скорость движения препарата возрастает, а его давление, в соответствии с уравнением Бернулли, падает. В смесительной камере возникает разрежение, и в нее засасывается атмосферный воздух. Всасывание происходит через одно из отверстий поворотного диска. Отверстия имеют различные диаметры. Выбирая соответствующее отверстие, регулируют состав смеси, подаваемой пациенту.

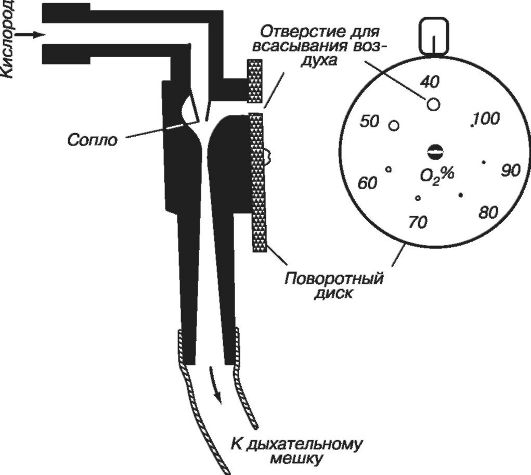Рис. 7.7.Подача кислорода при кислородной терапии

Ингалятор

Этот прибор используют для введения в область носоглотки лекарственных средств в распыленном виде (рис. 7.8).

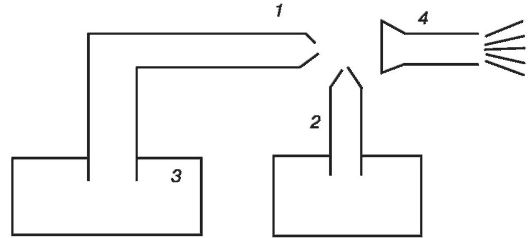Рис. 7.8.Схема ингалятора

Он состоит из двух трубок, расположенных под прямым углом.

Горизонтально расположенная трубка (1) имеет на конце сужение. Чуть ниже этого конца располагается верхний конец вертикальной трубки (2), нижний конец которой опущен в сосуд с жидким препаратом. В горизонтальную трубку подается пар (3). При прохождении суженного конца скорость пара возрастает, а давление падает. В область пониженного давления засасывается препарат, который распыляется струей пара. В результате образуется смесь пара, воздуха и капелек препарата, которая через патрубок (4) поступает к пациенту.

Основные понятия и формулы

Продолжение таблицы

7.6. Задачи

2.Кровь течет по горизонтальному участку артерии, имеющему сужение. Где давление крови на стенки сосуда будет больше - на суженном или широком участке? Динамическим или статическим давлением обусловлено фонтанирование крови при надрезе артерии?

Решение

Фонтанирование крови при надрезе артерии обусловлено разностью между статическим давлением в артерии и давлением атмосферы.

При прохождении места сужения скорость кровотока возрастает (7.2), а статическое давление, которое и воздействует на стенки сосуда, уменьшается (7.5). Отметим, что вклад динамического давления в полное давление ничтожен. Действительно, принимая v = 0,5 м/с, ρ = 10³ кг/м³, найдем:

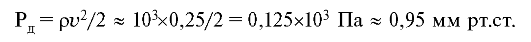Ответ: давление на стенки незначительно уменьшается на участке сужения артерии. Фонтанирование крови при надрезе артерии обусловлено статическим давлением.

3.Скорость потока крови в капиллярах равна примерно v₁= 30 мм/мин, а скорость потока крови в аорте v₂= 45 см/с. Определить, во сколько раз площадь сечения всех капилляров больше сечения аорты.

4.Лекарственный раствор вводят в мышцу животного с помощью шприца, внутренний диаметр которого d₁ = 10 мм, а диаметр иглы d₂ = 0,5 мм. Определить скорость истечения раствора из иглы, если скорость перемещения поршня шприца равна v₁ = 2,3 см/с.

7. Наблюдая под микроскопом эритроциты в капилляре, можно измерить скорость течения крови: v₁= 0,5 мм/с. Средняя скорость тока крови в аорте составляет v₂= 40 см/с. На основании этих данных определить, во сколько раз суммарная площадь поперечных сечений функционирующих капилляров больше площади сечения аорты.

Решение

Условие неразрывности струи было получено для трубки тока переменного сечения. Очевидно, что оно применимо и к разветвлению труб. В задаче такое разветвление начинается с аорты (площадь поперечного сечения S₂) и заканчивается капиллярами (общая площадь сечения S₁). Исходя из этого запишем уравнение неразрывности струи (7.2): S₁/S₂ = v₂/v₁= 800.

Ответ: 800.

8.При всасывании человек может понизить давление в легких на 80 мм рт.ст. ниже атмосферного. Определить, на какую высоту ему удастся втянуть воду по трубочке.

10.Во время бури или смерча с домов иногда срывает крыши. Используя уравнение Бернулли, объяснить, почему это происходит. Решение

Давление в потоке ветра уменьшается. Поэтому давление на чердаке превышает внешнее давление на величину ΔΡ = pv²/2. При этом на кровлю действует направленная наружу сила F = Spv²/2. При скорости v = 35 м/с (ураган), ρ = 1,3 кг/м³ и S = 100 м² величина силы составляет F = 61 000 Н (6 т), что существенно превышает вес кровли.

Линия тока. Трубка тока

При рас­смот­ре­нии ди­на­ми­ки дви­же­ния жид­ко­сти или газа можно не сле­дить за кон­крет­ной точ­кой среды, а сле­дить за кон­крет­ной точ­кой про­стран­ства и фик­си­ро­вать в таких точ­ках на­прав­ле­ние и ве­ли­чи­ну ско­ро­сти раз­лич­ных ча­стиц в дан­ный мо­мент вре­ме­ни. Таким об­ра­зом, в каж­дой точке про­стран­ства можно по­лу­чить неко­то­рый век­тор, име­ю­щий опре­де­лён­ную ве­ли­чи­ну и на­прав­ле­ние. Такая кар­ти­на на­зы­ва­ет­ся полем ско­ро­стей. В этом поле ско­ро­стей можно про­ве­сти неко­то­рые линии, линии тока (так же, как про­во­дят си­ло­вые линии в элек­три­че­ском или гра­ви­та­ци­он­ном полях) (см. рис .1).

Линия тока (на рис. 1 вы­де­ле­ны жёл­тым) – линия в про­стран­стве, на­прав­ле­ние ка­са­тель­ной к ко­то­рой в дан­ный мо­мент вре­ме­ни в каж­дой точке сов­па­да­ет с на­прав­ле­ни­ем век­то­ра ско­ро­сти в этой точке.

Рис. 1. Линии тока в поле ско­ро­стей

Если сде­лать мгно­вен­ное отоб­ра­же­ние, то можно поле ско­ро­стей за­ме­нить ли­ни­я­ми тока.

В том слу­чае, когда ско­ро­сти в дан­ной точке про­стран­ства не ме­ня­ют­ся со вре­ме­нем, такое дви­же­ние на­зы­ва­ют ста­ци­о­нар­ным дви­же­ни­ем жид­ко­сти или газа. В этом слу­чае кар­ти­на линий тока не будет за­ви­сеть от вре­ме­ни, она будет за­мо­ро­же­на. Линия тока в дан­ном слу­чаи будет пред­став­лять собой тра­ек­то­рию дви­же­ния от­дель­ной ча­сти­цы, ко­то­рая будет дви­гать­ся в каж­дый мо­мент вре­ме­ни в на­прав­ле­нии ка­са­тель­ных к этой линии.

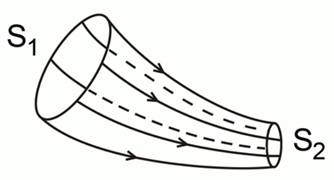
Рис. 2. Труб­ка тока

При ста­ци­о­нар­ном те­че­нии жид­ко­сти или газа из ста­ци­о­нар­ных линий тока можно по­стро­ить по­верх­ность такой формы, ко­то­рая на­зы­ва­ет­ся труб­кой тока (см. рис. 2). Эта труб­ка – мыс­лен­но вы­де­лен­ная труба, по ко­то­рой течёт жид­кость или газ (далее будет рас­смат­ри­вать­ся дви­же­ние жид­ко­сти имен­но в такой трубе). Если за опре­де­лён­ное время неко­то­рая масса жид­ко­сти пе­ре­тек­ла через по­верх­ность се­че­ния такой трубы , то такое же ко­ли­че­ство жид­ко­сти долж­но пе­ре­течь через се­че­ние трубы , так как с те­че­ни­ем вре­ме­ни пол­ная масса жид­ко­сти в этом объ­ё­ме, вы­де­лен­ным двумя се­че­ни­я­ми, ме­нять­ся не долж­на.