Нормальная и аномальная дисперсия и методы измерения

Если при увеличении длины волны l (уменьшение частоты w) показатель преломления n падает, то такой характер зависимости n = f(l) носит название нормальной дисперсии (рис. 8.1).

Рис. 8.1
Аналитический вид функции, описывающий такой характер зависимости, был предложен Коши:
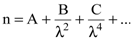, (8.7)
где А, В и С - константы, определяемые для каждого вещества из эксперимента.

Один из первых методов измерения дисперсии, получивший название метода скрещенных призм, был предложен еще Ньютоном (рис. 8.2)

Рис. 8.2
Суть метода состоит в том, что свет проходит последовательно через две призмы, преломляющие ребра которых перпендикулярны друг другу. Первая призма (Пр1), разлагая свет от источника (S), дает на экране Э₂ вертикальную полосу, которая проектируется на вторую призму (Пр2) и разлагается ею в горизонтальной плоскости. Причем угол отклонения зависит от длины волны падающего света, а величина отклонения определяется дисперсионными свойствами вещества второй призмы.

В общем случае зависимость показателя преломления вещества от длины волны может быть весьма сложной. Для определенных интервалов длин волн возможна зависимость nоказателя преломления n от l, обратная ходу нормальной дисперсии. В 1862 году Леру, наблюдая преломление в призме, наполненной парами йода, обнаружил, что синие лучи преломляются меньше красных. Эту особенность Леру назвал аномальной дисперсией.

Систематические исследования Кундта, который использовал метод скрещенных призм, показали, что явление аномальной дисперсии тесно связано с поглощением света - все тела, дающие аномальную дисперсию в какой-либо области, сильно поглощают свет в этой же области. Показатель преломления меняется вблизи полосы поглощения настолько быстро, что показатель преломления в точке А (меньшая длина волны l_А) меньше показателя преломления в точке В (большая длина волны l_В) (рис. 8.3).

Рис. 8.3
На рис. 8.3 интервалы длин волн от l₁ до l₂ (область 2) соответствуют области аномальной дисперсии, что совпадает с положением полосы поглощения вещества. Для излучения в спектральном интервале вне полосы поглощения (области 1 и 3) зависимость показателя преломления от длины волны соответствует нормальной дисперсии.

Рис. 8.4
Аномальная дисперсия наиболее отчетливо наблюдается для газов, характеризующихся резкими линиями поглощения и малыми концентрациями (что очень важно при изучении дисперсии в пределах полосы поглощения, когда интенсивность проходящего света резко падает). Из-за узости полос поглощения газов и паров наилучшие результаты наблюдаются с использованием интерферометра (Рождественского, Жамена) и скрещенного с ним призменного спектрографа (рис. 8.4).

Щель S₂ располагается в плоскости формирования интерференционных полос равного наклона, возникающих в результате прохождения лучей 1 и 2 через интерферометр (зеркала З₁ и З₂ имеют коэффициент отражения 50%, а зеркала З₃ и З₄ - 100%). Распределение интенсивности интерференционной картины представлено на рис.8.5. Оно определяется условием разности хода двух интерферирующих лучей

D21 = hsini×e = ml;

(8.8)

где i - угол падения лучей на зеркало З₁; h - база интерферометра; e- разность углов падения лучей, определяющих нулевой и m - й порядок интерференции. Причем в пределах одного порядка большим значениям e соответствует большее значение l. Щель спектрографа S₂ расположена перпендикулярно интерференционным полосам и выделяет лишь узкие участки интерференционной картины.

После прохождения света от щели S₂ через преломляющую призму спектрографа с нормальной дисперсией в исследуемой спектральной области произойдет пространственное разделение световых потоков разных длин волн одного порядка. Если оптическая система будет отрегулирована так, чтобы полоса нулевого порядка являлась осью симметрии всей интерференционной картины, на экране Э за спектрографом получится система полос, представленная на рис. 8.6, а нулевой порядок представлял бы собой прямую линию.

Рис. 8.6

Рис. 8.5
Ордината m-той полосы будет пропорциональна соответствующей разности хода ml, т.е. аналитически зависимость от длины волны может быть представлена как

y = aml,

(8.9)

где а определяется характером и параметрами применяемой оптической системы.

Если на пути одного из лучей интерферометра ввести слой вещества толщиной h с показателем преломления n = f(l), то интерферирующим лучам сообщается дополнительная разность хода, равная h(n-1). Уравнение, описывающее положение и вид кривых на экране, выразится соотношением

y = aml + ah(n-1) = am¢l.

(8.10)

Для полосы с m = 0 y = ah(n-1). Таким образом, нулевая полоса вычерчивает в определенном масштабе зависимость (n-1) от длины волны, т. е. дает непосредственно кривую дисперсии. Если в качестве исследуемого вещества ввести кювету с парами или газом, то можно исследовать ход зависимости показателя преломления от длины волны в области полосы поглощения, т. е. аномальную дисперсию.

Рис. 8.7
Рождественскому принадлежит важный метод измерения аномальной дисперсии. Поскольку ход аномальной и нормальной дисперсии противоположен, было предложено при введении в одно из плеч интерферометра кюветы с исследуемым веществом, обладающим аномальной дисперсией в некотором спектральном интервале, в другое плечо помещать кювету с веществом, обладающим нормальной дисперсией в этой области спектра. Для некоторой длины волны действие вещества с нормальной дисперсией будет точно скомпенсировано действием исследуемого вещества, так что в этом месте шкалы длин волн наклон интерференционной полосы пройдет через нуль. Слева от этого значения l кривые падают, а справа поднимаются (или наоборот), образуя крюк, положение вершины которого в шкале длин волн можно точно определить (рис. 8.7):

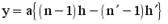,	(8.11)
.

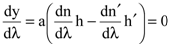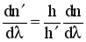Таким образом, зная характеристики вещества с нормальной дисперсией 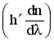, можно определить 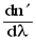для любого l, меняя толщину h (или h¢) и перемещая положение крюка по шкале длин волн. Этот метод «крюков» Рождественского широко используется для точных измерений дисперсии.
8.2. Электронная теория дисперсии

Основные черты теории дисперсии были описаны Зельмеером (1871) и основывались на представлении о взаимодействии между молекулами среды и эфиром. Особенностью его теории было допущение, что молекулы обладают собственными частотами колебаний, характерными для данного вещества. Наличие таких частот приводит к зависимости показателя преломления n от частоты падающего света w, хорошо передающей весь ход кривой дисперсии как вблизи, так и вдали от полос поглощения. Измерения n отlдля паров натрия Рождественским дали хорошее согласие теории и эксперимента.

В теории дисперсии Зельмеера удалось связать оптическую константу (скорость света в веществе v) с другими параметрами вещества и, прежде всего, с собственными частотами колебаний его молекул w_о. В настоящее время теория дисперсии строится на электронном толковании строения атомов и молекул в совокупности с использованием понятия их собственных колебаний.

Сущность взаимодействия света с веществом сводится к интерференции падающей (первичной) волны с вторичными волнами, возникающими вследствие колебаний электрических зарядов вещества (прежде всего электронов из-за малости их массы), приведенных в движение полем первичной волны.

Исследуем зависимость диэлектрической проницаемости среды от частоты световых волн, проходящих через нее и вызывающих смещение электрических зарядов вещества. Поскольку 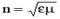(m=1 для немагнитных сред), то несложно перейти и к зависимости отl.

Под влиянием внешнего поля заряды смещаются от положения равновесия на расстояние r, превращая, таким образом, атом в электрическую систему с электрическим дипольным моментом 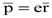, направленным вдоль поля. Если в единице объема находится N атомов, то электрический момент единицы объема 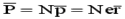. При этом будем предполагать, что в среде имеется лишь один сорт атомов и в каждом из них способен смещаться только один электрон. В противном случае поляризация среды выразилась бы в виде

,

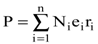(8.12)

где i относится к i-му сорту зарядов. Зная P, нетрудно связать его значение с диэлектрической проницаемостью, ибо

D = eeoE = eoE + P.

(8.13)

Задача сводится к определению характера и величины смещения r от частоты вынуждающей силы w и собственной частоты колебаний w_оэлектронов в среде под действием внешнего поля световой волны. При этом следует иметь в виду, что речь идет об электронах, частоты колебаний которых порядка частот световой волны. Такие электроны называются оптическими.

Общее уравнение, описывающее характер движения электронов под действием внешнего электрического поля световой волны, определяется следующим соотношением:

,

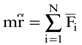(8.14)

где m - масса электрона.

Для рассмотрения основных черт дисперсии достаточно в выражении (8.14) учесть три силы, действующие на электроны.

1. Удерживающая, квазиупругая сила

,

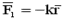(8.15)

где k - коэффициент квазиупругости.

Опыт показывает, что изолированные атомы всех веществ способны излучать монохроматические волны с характерными для каждого вещества частотами, поэтому удерживающая электрон в атоме сила должна носить квазиупругий характер.

2. Поскольку предположение о гармоническом колебании имеет приближенный характер, то целесообразно ввести силу, уменьшающую амплитуду колебания и приводящую к его затуханию:

.

(8.16)

Формула (8.16) отождествляет силу затухания с силой трения, величина которой во многих случаях движения тела в среде пропорциональна скорости движения. Исследование различных физических причин затухания колебаний электронов в веществе показывает, что они во многом согласуются с тормозящей силой.

3. Вынужденные колебания электрона возникают под действием световой волны, распространяющейся в среде. Выше указывалось, что, если не оговаривать специальных условий, при рассмотрении такой силы следует учитывать лишь электрическую составляющую световой волны (силу Кулона)

.

(8.17)

В качестве внешнего светового поля возьмем поле плоской волны, что является хорошим приближением для выяснения основных черт теории дисперсии:

.

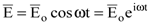(8.18)

Тогда общее уравнение дисперсии запишется при учете действия всех вил вдоль 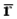в виде

.

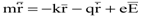(8.19)

Учитывая безынерционность электрона, можно утверждать, что характер изменения положения равновесия электрона будет соответствовать характеру внешнего поля, и одним из частных решений уравнения (8.19) будет

r = roeiwt.

(8.20)

Из условий (8.19) и (8.20) определим амплитуду колебаний электрона r_o

,

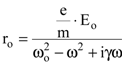(8.21)

где 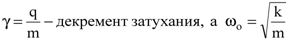- собственная частота колебания электронов.

С учетом значения r и Е в (8.22), определим зависимость показателя преломления среды от частоты, т.е. дисперсию вещества ee_оЕ = e_оЕ + Р или ee_оЕ_ое^iwt = e_оЕ_ое^-iwt + Ner_oe^iwt. Подставив r_o, получим

.

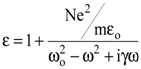(8.22)

Поскольку n² = e, то окончательно

.

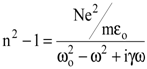(8.23)

Выражение (8.23) называется уравнением дисперсии и определяет зависимость показателя преломления среды n от частоты w в области нормальной и аномальной дисперсии.
8.3. Нормальная дисперсия

Дисперсия в области прозрачности вещества (вдали от линии поглощения) - нормальная дисперсия. Для этого случая g=0. Тогда выражение (8.23) примет вид

.

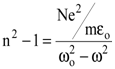(8.24)

На рис. 8.8 представлен график зависимости n²-1 от частоты внешнего поля w:

а) приw<w_о n²-1 растет с ростом w;

б) при w>w_о n²-1 растет с ростом w.

Обычно w_о>>w, и

n2-1= ,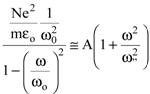

(8.25)

Рис. 8.8
где 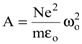. Учитывая, что 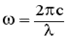, формулу (8.25) перепишем

n²-1= .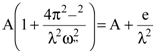

Для газов n²-1=(n-1)(n+1)@2(n-1)= = 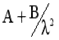. Тогда

,

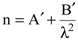(8.26)

где 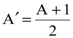, а .

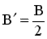Формула (8.26) носит название формулы Коши.
8.4. Дисперсия вблизи линии поглощения (аномальная дисперсия)

Анализ (8.24) показывает, что график n²-1 от w имеет разрыв при w=w_о. Показатель преломления в этой точке стремится к ¥, что лишено физического смысла и является результатом упрощенного предположения об отсутствии сопротивления движению (g=0). Поскольку затухание связано с областью частот w, близких к собственной частоте колебаний вещества w_о, и в области собственной частоты ход зависимости n²-1 от w будет иным, нежели в отсутствии затухания.

Поскольку уравнение (8.23) справа представляет собой комплексную величину, то оно будет иметь смысл, если выражение слева в (8.23) n²-1 также будет величиной комплексной. Введение комплексного показателя преломления несет в себе вполне определенный смысл, так как связывает наличие аномальной дисперсии с поглощением света. Если представить показатель преломления в виде

n¢ = n(1-ic),

(8.27)

то, как было показано выше, распространение плоской волны Е = Е_ое^{i(wt - kx)} в среде с таким n определяет условие ее затухания.

Введя комплексный показатель преломления n¢ = n(1-ic) в уравнение дисперсии и разделив действительные и мнимые части, получим два уравнения, определяющие характер дисперсии вблизи линий поглощения:

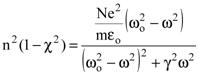;	(8.28)
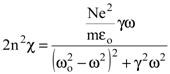.	(8.29)

Уравнение (8.28) дает ход зависимости e от частоты w. Нетрудно убедиться, что у кривой, описываемой этой формулой, существует два экстремума, определяющие области нормальной и аномальной дисперсии. Эти точки задаются соотношением

,

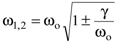(8.30)

где w_о-собственная частота колебаний, а g- декремент затухания. Исследовав значение второй производной в точках w₁ и w₂, легко убедиться, что области частот от w = 0 до w = w₁ и от частот w = w₂до w = ¥ соответствуют нормальной дисперсии, а интервал частот от w₁ до w₂, задающийся (8.29), соответствует аномальной дисперсии. Величина интервала частот аномальной дисперсии пропорциональная значению декремента затухания g и напрямую связана с шириной полосы поглощения. Нетрудно убедиться, что соотношение (8.29) описывает зависимость показателя поглощения от частоты. Максимум поглощения приходится наw = w_о и равен

.

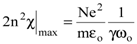(8.31)

Если определить значение величины 2n²c на частотах w₁ и w₂, соответствующих разделению областей нормальной и аномальной дисперсии, то величина 2n²c будет равна половине максимального значения, т. е.

.

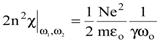(8.32)

Рис. 8.9
Интервал частот, соответствующий значениям поглощения, равным половине максимального, носит название ширины полосы поглощения. Область аномальной дисперсии, связанной с процессом поглощения света, лежит в пределах ширины полосы поглощения, определенной (8.30). На рис. 8.9 приведены график кривой дисперсии и полосы поглощения вещества.

Если принять во внимание, что в веществе может быть несколько сортов зарядов, способных к колебаниям с различными собственными частотами w_оiи массой m_i, то формула для дисперсии (8.33) выразится

.

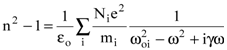(8.33)

Формулу (8.33) можно переписать по-другому, введя величину f_i, называемую силой осциллятора и характеризующую степень участия осцилляторов одного сорта в процессе взаимодействия излучения со средой.

Пусть N_i=Nf_i, где N_i – число осцилляторов в единице объеме с частотой w_оi, а N - общее число осцилляторов в единице объема.

Тогда

.

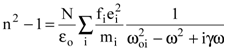(8.34)

Рис. 8.10

В этом случае дисперсионная кривая будет иметь несколько областей аномальной дисперсии, соответствующей каждому w_оi (рис.8.10).
8.5. Учет действия молекул окружающей среды

При рассмотрении физических основ дисперсии предполагалось, что действующее на колеблющийся электрический диполь поле 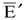связано лишь с полем внешней световой волны 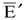= 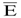. Однако для жидкостей, твердых тел и плотных газов необходимо учитывать добавку, связанную с возникновением поля поляризованных зарядов среды под действием наведенного поля электрического диполя. Для простейшего случая изотропного распределения вещества связь между 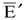, 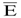и поляризацией 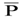определяется как

.

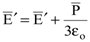(8.35)

Таким образом, уравнение движения электрона под действием внешнего поля без учета затухания будет выглядеть несколько иначе:

.

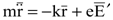(8.36)

или, переходя от векторных значений к величинам,

.

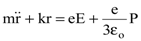(8.37)

Умножив (8.37) на eN и заменяя eNr через Р, находим

.

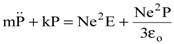(8.38)

С учетом того, что 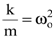и Р = Р_ое^iwt, из соотношения (8.13) определим n²:

.

(8.39)

Преобразуя выражение (8.39), получим

,

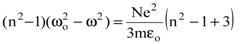или

.

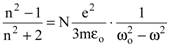(8.40)

Эта формула носит название Лоренц-Лорентца и была получена в 1880 г. обоими учеными независимо друг от друга. Если считать величины e, m, w_о постоянными для данного вещества, то для определенной частоты w формула Лоренц-Лорентца примет вид:

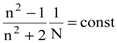
или через плотность вещества r:

.

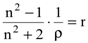(8.41)

Выражение (8.41) носит название удельной рефракции вещества и не зависит от его плотности.

Рефракцию смеси вещества R можно вычислить, если известны рефракции r₁, r₂ ... его отдельных компонент и их процентное содержание с₁, с₂ ... в смеси

100R = c1r1 + c2r2 + ... .

(8.42)

Еще большее значение имеет правило, согласно которому рефракцию сложного химического соединения можно вычислить, складывая рефракцию элементов, его составляющих. Для каждого элемента вводится понятие атомной рефракции, равной произведению атомного весаа на его удельную рефракцию r. Если молекулярный вес М, а удельная рефракция молекулы R, то

MR = q1a1r1 + q2a2r2 + ...

(8.43)

где q - число атомов данного элемента, входящих в молекулу.
8.6. Дисперсия рентгеновских лучей

Для рентгеновского излучения частота поля w значительно превышает w_о вещества и формула дисперсии (без учета затухания) представится в виде

.

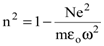(8.44)

Таким образом, показатель преломления рентгеновских лучей меньше единицы. Для стекла при длине волны 0,1 нм n - 1 - 1×10^-6. Это обстоятельство (n<1) позволяет осуществлять в рентгеновской области явление полного отражения на границе воздух-стекло. Изменяя длину волны рентгеновского излучения, можно наблюдать и аномальную дисперсию рентгеновских лучей вблизи характеристических частот вещества, как собственные частоты электронов.
8.7. Дисперсия на свободных электронах

Прохождение света через ионизированную среду сопровождается взаимодействием свободных носителей заряда с электромагнитной волной. В этом случае уравнение движения электрона (без учета затухания) примет вид:

.

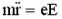(8.45)

Решение этого уравнения при условиях, оговоренных выше, формально примет вид, как и выражение (8.44).

Определим 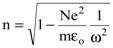с учетом того, что 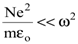. Тогда 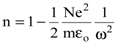. Подобная ситуация может осуществиться в верхних слоях атмосферы на границе ионизированный слой атмосферы - вакуум, где возможно значительное отражение для радиоволн, т.к. n<1. Эффективность такого отражения зависит от плотности ионизированных частиц и может меняться для различных частот w электромагнитной волны при различных факторах, приводящих к ионизации. Для частот w, приближающихся к частоте

,

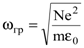(8.46)

показатель преломления n стремится к 1 и распространение более коротких электромагнитных волн в атмосфере пройдет без преломления и отражения.
8.8. Ширина и форма спектральных линий

При свободном колебании осциллятора с частотой w_о, благодаря излучению, электромагнитная волна уносит с собой энергию. Очевидно, что изменение энергии осциллятора в единицу времени определится с учетом (2.67)

.

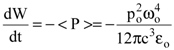(8.47)

Полная энергия электрического диполя равна

,

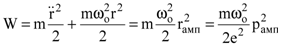(8.48)

где q – заряд электрона, p_амп- амплитудное значение дипольного момента .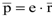

Подставляя в (8.47) W из (8.48), получаем

,

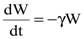(8.49)

где .

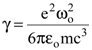Рис. 8.11
Поскольку решение (8.49) имеет вид 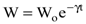, то энергия колеблющегося электрического диполя уменьшается со временем по экспоненциальному закону (рис. 8.11), причем при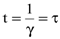 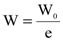. Величина 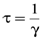носит название времени жизни осциллятора при свободном излучении. Для частот излучения видимого света w=4×10¹⁵ с^-1 можно оценить 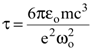. Подставляя численные значения в формулу, получим t@10^-8 с.

Амплитуда колебания электрона в соответствии с (8.48) и (8.49) изменяется по закону

,

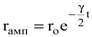(8.50)

где r_o – амплитуда колебания в начальный момент времени (t=0).

Тогда отклонение электрона от положения равновесия в любой момент времени t будет описываться формулой

,

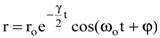(8.51)

явлющейся решением уравнения

.

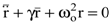(8.52)

Это уравнение описывает характер колебания электрического диполя при условии слабого затухания (g<<w_о).

Поскольку излучение диполя затухающее, то колебание, описываемое формулой (8.51) не является периодическим процессом. Затухающий осциллятор излучает сплошной спектр, характер которого можно определить путем разложения в интеграле Фурье, где интегрирование идет по всевозможным частотам от-¥ до ¥. В результате такого разложения можно получить спектральное распределение I(w) гармонических составляющих, определяющих структуру спектральной линии. Учитывая, что полная интенсивность I_o излучения затухающего осциллятора определится как

,

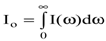(8.53)

Связь между I(w) и I_oна частоте w представится формулой

.

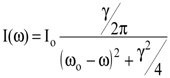(8.54)

На частотах 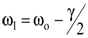и 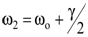I(w) будет в 2 раза меньше интенсивности излучения приw=w_о, т.е. основная часть излучения будет приходиться на интервал Dw=w₂-w₁=g, называемый шириной линии излучения.

Формулу (8.54) можно представить в виде

,

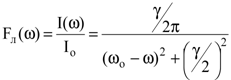(8.55)

называемой нормированной функцией лоренцевой формы линии излучения. Лоренцева форма линии излучения образуется при условиях, когда затухание колебания элементарного осциллятора происходит за счет излучения. Поэтому такая форма линии называется естественной формой линии излучения. Поскольку для оптических частот , то естественная ширина линии излучения очень мала, и поэтому можно считать, что все излучение приходится на очень узкий интервал частот вблизи w_о, т.е. оно монохроматическое.

Если колеблющийся электрон находится в поле падающей световой волны 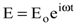, то его уравнение движения описывается выражением (8.19), а решение задается формулой r=r_oe^iwt с учетом (8.21).

Интенсивность поглощения пропорциональна квадрату амплитуды, т.е. 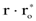. Если на упругосвязанный электрон падает излучение с непрерывным спектром частот, то возникает поглощение с коэффициентом, задающимся формулой (8.31).

Распределение поглощенной энергии как функции частоты при условии w_о<<g (для разреженных газов) можно представить в виде

,

(8.56)

Линия поглощения имеет лоренцову форму с той же шириной, что и линия излучения. В реальных условиях ширина спектральных линий значительно более естественной вследствие хаотичного теплового движения и взаимодействия атомов друг с другом.

Существует два типа факторов, приводящих к уширению линий излучения – однородному и неоднородному. Однородное уширение определяется одинаковыми изменениями линий излучения у различных атомов. Другая группа факторов вызывает в излучении отдельных атомов различные изменения линий излучения.

К однородному уширению относится естественная ширина линий излучения, поскольку уширение и форма в этом случае одинаковы для всех атомов.

Примером однородного уширения является ударное, поскольку оно характеризуется средним промежутком t между столкновениями, одинаковыми для всех частиц. Взаимодействие частиц вследствие соударения в газах при комнатной температуре и нормальном давлении приводит к уменьшению времени жизни частиц на два порядка, что соответствует такому же уширению линии испускания по сравнению с естественной шириной при сохранении лоренцевой формы.

Примером неоднородного уширения линии излучения является доплеровское уширение, связанное с изменением частоты излучения атома вследствие своего движения. При нерелятивистских скоростях частиц зависимость частоты w от v выразится формулой

,

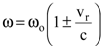(8.57)

где w_о-собственная частота колебания частицы, v_r – скорость ее движения вдоль линии, соединяющей источник и наблюдателя. Причем знак «+» соответствует движению частицы к наблюдателю, а «-» от наблюдателя. Нетрудно показать, что в этом случае плотность энергии излучения как функция частоты будет описываться функцией, дающей гауссову форму линии

.

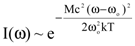(8.58)

Максимум интенсивности приходится на частоту w=w_о, а ширина

.
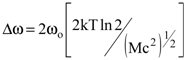